基于稀疏表达的图像去噪方法研究

陈 柘， 陈 海

（1.长安大学 信息工程学院，陕西 西安 710064；2.西安交通大学 软件学院，陕西 西安 710049）

基于稀疏表达的图像去噪方法研究

陈 柘1， 陈 海2

（1.长安大学 信息工程学院，陕西 西安 710064；2.西安交通大学 软件学院，陕西 西安 710049）

提出一种基于混合字典的图像稀疏分解去噪方法。使用小波包函数和离散余弦函数构成混合字典，采用匹配追踪算法对图像进行稀疏分解，提取含噪图像中的稀疏成分，最后利用稀疏成分进行图像重构，达到去除图像中噪声的目的。实验中与单一字典稀疏分解去噪算法进行了对比，结果表明，所提出的混合字典稀疏去噪算法可有效提取图像中的稀疏结构，改善重构图像的主客观质量。

图像去噪；稀疏表达；混合字典；匹配追踪

人类大脑视觉皮层神经元在响应自然图像信号时，只有个别神经元处于活跃状态，大部分神经元没有响应。这一特点启发人们提出了图像的稀疏表示方法[1-2]，即用一组基函数来模拟人类大脑视觉皮层的神经元。该方法类似于傅里叶分析和小波分析，图像被表示为基函数的线性组合，但有所不同的是，图像在这组基函数上的展开系数大部分为零，只有少部分为非零系数。这里，基函数被称为原子，原子的集合称为字典。为了实现稀疏表示，用于表达图像的字典通常是超完备的。

稀疏分解能够将信号的能量集中在少数系数上，这不仅有利于信号的压缩、编码，同样也适用于从图像中去除噪声。其原因在于：由于图像信号中存在的自相似性，理想非含噪信号可以稀疏表示，而噪声由于不具有结构性，无法稀疏表示。所以，对含噪图像而言，若将其进行稀疏分解，那么稀疏成分将对应于理想信号，含噪图像与稀疏成分的残差则对应于噪声[3]。利用这个特点，通过稀疏分解提取含噪图像中的稀疏成分，而后利用稀疏成分重构图像，就可以达到去除噪声的目的。

目前，在基于稀疏表达的图像去噪方法研究中，焦点集中在字典设计和稀疏重构算法上。字典中基的选择一般可通过三种途径实现：正交基，如傅立叶基、小波基；紧框架，如各种多尺度几何分析方法；冗余字典，如Gabor多成分字典等。典型的稀疏重构算法有基于范数最小化的贪婪算法，如匹配追踪[4]、正交匹配追踪[5]等；基于范数最小化的线性规划算法，如基追踪法[6]、梯度投影稀疏重构[7]等；以及统计优化重构算法，如 Bayes 重构[8]。

本文讨论了稀疏表达去噪的一般原理，针对一般单一字典稀疏表达的局限性，提出一种基于混合字典的稀疏去噪方法。使用小波包函数和离散余弦函数构造超完备字典，采用匹配追踪算法提取图像中的稀疏结构，最后利用提取的稀疏结构重构图像。实验结果表明，提出的稀疏去噪算法可有效提取图像中的稀疏结构，改善重构图像的主客观质量。

1 稀疏表达图像去噪一般框架

与完备正交基信号分解不同，稀疏表达借用超完备冗余基来建立信号的表达。稀疏表达是将信号在冗余基上线性展开，并在字典中选择能够最稀疏地表达信号的原子组合。对于加性高斯白噪声模型

y，x，v∈RN×1，y 为观测向量，x 代表信号，v～N（0，σ）为零均值高斯白噪声。构造超完备冗余字典D∈RN×K，其中K＞N，表明D中的基向量是超完备冗余的。对于观测信号y，可以用字典D中原子的线性组合近似表示，即

α表示系数，dk是超完备字典D中的一个原子。这里，表达的稀疏性要求＾在最接近于y时，系数矩阵α是最稀疏的。即，需要求得α的一个稀疏解，使＾与y之间的误差最小，如式（3）所示。

是范数，表示向量或矩阵中非零元素的个数，为误差因子。如果将约束项转化为惩罚项，式（3）可进一步表示为

式中，μ称为惩罚因子。

去噪过程包括以下两个步骤，首先求得信号的稀疏分解，再使用分解系数重构图像，该过程可用如下两式表示：

式（5）表示求解y所对应的稀疏解，即提取y中的稀疏成分；式（6）利用获得的稀疏成分重构图像，得到去噪后的图像。

为提高运算速度，通常将图像分块处理。即首先将图像划分为若干大小为的子块，而后对每一子块分别进行稀疏分解和重构，最后将重构后的子块拼接构成整幅重构图像。这时的优化问题可表述如下[9]：

这里I和Inoisy分别表示原始无噪图像和被噪声污染后的图像，Ri，j为子图提取算子，表示从图像中提取第ij张子图。式中第一项衡量含噪图像与原始图像的总体相似度，第二项是稀疏性约束，第三项表示重构子图与原始图像中相对应的子图间的误差。

当给定字典D，可首先对每张子图进行稀疏分解，得到[9]

当求得所有子图的稀疏表示后，式（7）所表示的优化问题转化为[9]

2 基于混合字典的稀疏表达图像去噪

目前，在图像稀疏表达中多使用单一信号分解方法构造超完备冗余字典。但由于单一字典表达的局限性，不利于充分提取图像中的稀疏结构。为克服这一缺点，本文使用多重信号表达构造超完备字典，采用匹配追踪算法对图像进行稀疏分解，经重构后获得去噪后的图像。

2.1 字典构造

由于单一信号表达方法的局限性，本文尝试使用多重信号表达方法构造超完备冗余字典。基于小波变换良好的时频特性和离散余弦函数对纹理特征表达的有效性，本文将两种表达方法做了组合，共同构成超完备字典。

离散余弦字典可由下述方法构成：

这里，φk（n）表示第k个原子，N为信号序列的长度。

小波包字典中的原子由尺度、平移和频率3个参数确定，通常由一组尺度函数和小波函数经变换而成。处于不同尺度的函数可由二尺度方程确定，即

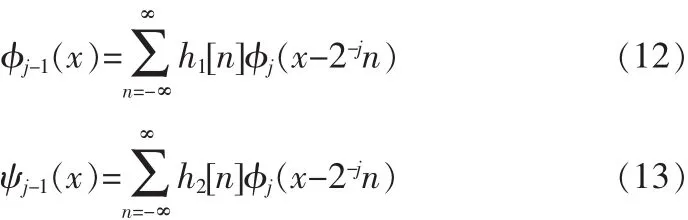
h1和h2为一组共轭对称滤波器。本文选取Daubechies最小非对称小波包函数作为基函数，该函数具有近似对称性和正交性，如图1所示。

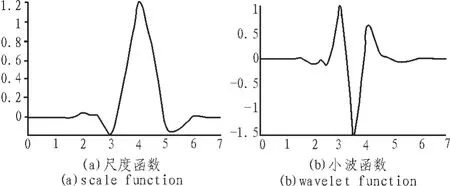
图1 Daubechies最小非对称小波包函数Fig.1 Daubechies least asymmetric wavelet packet function

2.2 稀疏分解

匹配追踪算法是稀疏分解的典型算法，具有计算简捷的特点。其基本思想是通过多次迭代从字典中获取与残差信号最匹配的原子组合，当逼近误差达到一定范围或经过指定迭代次数后算法结束。

匹配追踪算法遵循以下步骤：

步骤 1.初始化。 假设有字典 D={φγ}γ∈Γ，Γ 为指标集。 对于信号f，做初始分解得

这里，Rf表示对f的逼近残差。

步骤2.迭代运算。为使‖Rf‖最小化，每次迭代都从字典D中选取使得‖Rf‖最小的原子φγi，i表示迭代次数。经N次迭代后，可获得f的第N次逼近

令R0f=f，Rif表示第i次迭代后的逼近残差。

步骤3.停止规则。当残差能量小于给定数值时，迭代结束。否则，继续步骤2。

文献[3]中已经证明，当迭代次数趋于无穷时，逼近残差接近于零。实际使用中，可通过指定最小逼近误差或者最大迭代次数来使迭代终止。

2.3 稀疏重构

稀疏重构是指，使用求得的最稀疏解，按照式（6）求解原始信号的估计值。

3 实验与结果分析

图2 稀疏分解去噪算法性能对比Fig.2 Performance comparison of different sparse decomposition image denoising

为验证算法的有效性，选取一组标准测试自然图像，通过加入均值为零，标准差为的高斯白噪声，使用本文的稀疏分解去噪算法进行去噪处理，并与使用单一离散余弦表达的字典稀疏分解算法做对比，结果如图2所示。实验中，首先将图像分块，分块大小为，而后对每个分块进行矢量化，即将每一小块图像转化为一维矢量，之后按第2节所述方法做稀疏分解和重构，最后将重构后的分块图像进行拼接处理。本文取为，为噪声的标准差。图2（a）为原始的Barbara图像，图2（b）是加入高斯白噪声后的图像，这里，噪声标准差取为20。图2（c）为单一DCT表达字典去噪结果，图2（d）为本文方法的去噪结果。为便于观测对比，将图2（c）和（d）的做了局部放大，分别显示在图2（e）和（f）中。经过主观对比发现，本文的去噪算法能更好地去除图像中的噪声，并保留图像中的纹理等细节成分。

除主观评价外，为客观分析重构图像质量，选用峰值信噪比作为图像重构质量指标，PSNR=10lg（2552/MSE），这里，MSE表示原始图像和稀疏重构后图像的均方误差。计算结果发现，单一DCT字典稀疏分解去噪的PSNR为27.2，本文的PSNR达到28.3，同样说明本文方法可进一步提高重构图像的质量。

4 结束语

本文组合使用离散余弦变换和小波包变换构成超完备冗余字典，在同样使用匹配追踪算法进行稀疏分解时，可进一步降低信号的逼近残差。原因在于，多重表达方法可有效弥补单一表达的局限性，可更好地提取图像中的稀疏结构，从而提高重构图像质量。实验结果说明了本文方法的可行性和有效性。如何提高组合表达的性能，实现优化组合，将是本文后续的研究目标。

[1]Elad M.Sparse and Redundant Representations:From Theory to Applications in Signal and Image Processing[M].Berlin:Springer Verlag，2010.

[2]薛男，凌霖，陶晓洋，等.基于压缩感知的信号重构[J].电子设计工程，2013，21（7）:34-36.

XUE Nan，LING Lin，TAO Xiao-yang，et al.Signal reconstruction basedoncompressivesensing[J].ElectronicDesignEngineering，2013，21（7）:34-36.

[3]尹忠科，解梅，王建英.基于稀疏分解的图像去噪[J].电子科技大学学报，2006，35（6）:876-878.

YIN Zhong-ke，XIE Mei，WANG Jian-ying.Image denoising based on its sparse decomposition[J].Journal of University of Electronic Science and Technology of China，2006，35 （6）:876-878.

[4]Mallat S G，Zhang Z.Matching pursuit with time-frequency dictionaries[J].IEEE Trans.on Signal Processing，1993，41（12）:3397-3745.

[5]Tropp J A，Gilbert A C.Signal recovery from random measurements via orthogonal matching pursuit[J].IEEE Trans.on Information Theory，2007，53（12）:4655-4666.

[6]Chen S S，Donoho D L，Saunders M A.Atomic decomposition by basis pursuit[J].SIAM Review，2001，43（1）:129-159.

[7]Elad M，Aharon M.Image denoising via sparse and redundant representations over learned dictionaries[J].IEEE Trans.on Image Processing，2006，15（12）:3736-3745.

[8]Heijmans H J A M，Goutsias J.Nonlinear multiresolution signal decomposition schemes-Part II:morphological wavelet[J].IEEE Trans.on Image Processing，2000，9（11）:1897-1913.

[9]蔡泽民，赖剑煌.一种基于超完备字典学习的图像去噪方法[J].电子学报，2009，37（2）:347-350.

CAIZe-min，LAIJian-huang.An overcomplete learned dictionary-based image denoising method[J].ACTA Electronica Sinica，2009，37（2）:347-350.

Research on image denoising based on sparse representation

CHEN Zhe1，CHEN Hai2
（1.School of Information Engineering， Chang'an University， Xi’an 710064， China；2.School of Software， Xi'an Jiaotong University， Xi’an 710049， China）

A sparse representation image denoising method based on mixed overcomplete dictionary is proposed.Firstly，overcomplete dictionary is composed by mixing wavelet packet and discrete cosine function.And then matching pursuit algorithm is used to decompose image and extract sparse components.Finally，image is reconstructed using these sparse components.By doing so， the noise in the image is reduced.In the experiment， the proposed algorithm is compared with the common used unitary dictionary sparse representation method，and the results show that the proposed method can effectively extract sparse component of the image and improve the subjective and objective image quality.

image denoising； sparse representation； mixed dictionary； matching pursuit

TP319

A

1674-6236（2014）02-0168-03

2013-06-03 稿件编号：201306010

中央高校基本科研业务费专项资助项目（CHD2010JC027）

陈 柘（1969—），男，陕西西安人，博士。研究方向：图像处理、模式识别。