一种改进的步进频率雷达信号的运动补偿研究
2014-09-23王蒙军
段 宏 ,王 霞 ,王蒙军
(1.河北工业大学 信息工程学院,天津 300401;2.63813部队 海南 文昌 571300)
一种改进的步进频率雷达信号的运动补偿研究
段 宏1,2,王 霞1,王蒙军1
(1.河北工业大学 信息工程学院,天津 300401;2.63813部队 海南 文昌 571300)
为解决步进频率雷达一维距离像失真和运动补偿的问题,提出了一种精确的速度估计方法。文中首先阐述了步进频率信号的改进原理及其处理方法,该方法先使用互相关FFT测速法对目标速度进行粗估计,然后再以最大脉组乘积求和为准则搜索精确速度,最后实现对运动目标的速度补偿从而得到精确的一维距离像。仿真结果表明,在信噪比为-4dB的时候仍能得到准确的结果,改进后的信号性能有了很明显的改善,一维距离像不会随目标的运动而产生失真,该运动补偿方法具有估计精度高、抗噪性能好的优点。
步进频率;一维距离像;运动补偿;互相关函数;最大脉组乘积求和法
步进频率雷达信号是获得高分辨率距离像的一种重要信号,其基本原理是发射一组载频线性跳变的脉冲串,利用逆傅里叶变换(IFFT)对回波进行处理,从而获得高分辨的效果。由于连续发射的脉冲串能获得足够的带宽,因此可降低对瞬时带宽的要求,因此近年来得到广泛应用。然而这种信号的主要问题是存在距离一速度藕合,目标运动会使回波信号产生附加相位项,使得一维距离像产生时移、衰减、发散、波形展宽、散射点分裂等现象,导致一维距离像严重失真,影响目标的检测、识别和精确测速。
目前国内外学者已对速度补偿问题做了一些研究工作。文献[1]提到的时域互相关法存在测速误差大的问题;频域相关法无模糊测速范围较小;最小波形熵法计算量大,在信噪比低的条件下搜索易失败。文献[2]提到的最小脉组误差法单独使用时存在局部极小值问题。文献[3-4]中提到的基于评价函数的方法存在计算复杂,工程上难以实现的问题。文献[5]采用了改变雷达信号体制方法,具体是利用SF+PD(stepped frequency+pulse Doppler,步进频率+脉冲多普勒)的体制,此方法只利用了一半的信号能量,因此雷达工作效率较低。针对上述问题,为进行合理的运动补偿,本文利用一种改进的步进频率雷达信号先消除由于目标运动而产生的二次相位项对一维距离像的影响。并在此基础上,提出首先利用回波序列互相关函数快速傅里叶变换对速度进行粗估计实现速度粗补偿,然后利用最大脉组乘积求和法实现速度精确测量,以获得运动目标精确的一维距离像。
1 步进频率信号改进原理与处理方法
1.1 步进频率信号的改进原理
常规步进频率信号的时域数学表达式如式(1)所示:
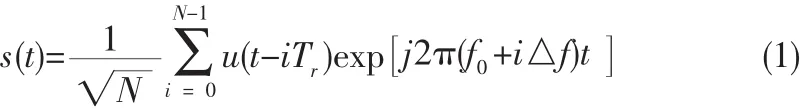
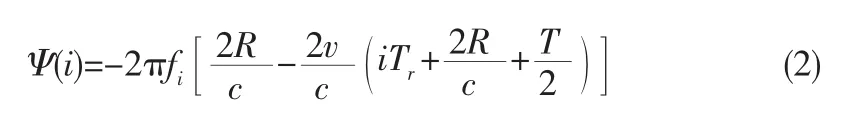
式中R为雷达到目标的径向距离,v为目标的径向速度,c为光速。


由此可推知,相邻的两个脉冲回波信号间的相位关系为:

式(4)为一常数,因此不同周期子脉冲间的相对相位关系不发生变化,不会使一维距离像产生失真,只会使距离像产生游动,由此可见根据式(3)设计的步进频率信号能使目标一维距离像不产生失真。改进后的步进频率信号的时频域波形如图1所示。

图1 脉冲重复时间改变的步进频率信号波形图Fig.1 The waveform stepped-frequency signal of pulse repetition time change
1.2 改进后的步进频率信号处理方法

去掉对一维距离像没有影响的固定相位项,经过整理后可得:


2 改进后步进频率信号的速度补偿
根据前面的理论分析可知,改进后的信号在目标匀速运动的情况下不会引起距离像失真,但是一维距离像会发生时移,无法为信号的继续处理提供准确的信息。因此要想得到精确的一维距离像,必须对目标回波进行速度补偿。
2.1 改进后步进频率信号的速度粗补偿
本文使用基于互相关函数FFT的速度估计方法来进行速度的粗估计,其具体计算步骤如下[7]。
交替发射两组改进后的脉冲串,第一组发射脉冲载频从f0正向步进到f0+(N-1)△f;第二组发射脉冲载频从f0+(N-1)△f负向步进到f0。取相邻两正向步进的脉冲串,雷达接收后经信号处理系统进行采样归一化处理后可得:

将这两个序列进行互相关处理得:
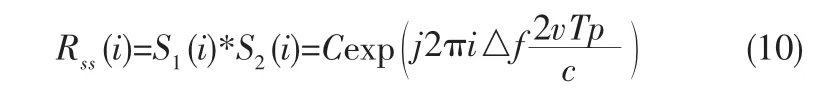


2.2 改进后步进频率信号的速度精确补偿
根据上面的分析,基于互相关函数FFT的粗速度估计方法只能得到一个离散的速度段,为了更精确地估计目标速度,本文利用最大脉组乘积求和法来搜索目标的精确速度,具体推导步骤如下[8]:
连续取一组正向步进和一组负向步进的脉冲串,此时这两组改进后步进频率信号的回波为:

其中,△v=V-v,V为目标速度的真实值,v为目标速度的估计值。
本文选取最大脉组乘积求和函数为准则来搜索最佳的估计速度,其定义式为:
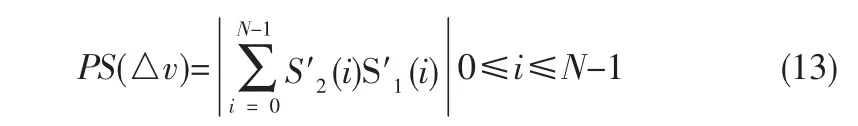
式中△v=0当时,PS(△v)达到全局最大值,此时估计速度与目标真实速度相等。为进行抗噪性能的比较分析,本文将脉组相位差分法、脉组误差法和最大脉组乘积求和法的性能进行了对比,图2是在时域信噪比SNR=-10 dB的情况下3种方法的性能比较结果。
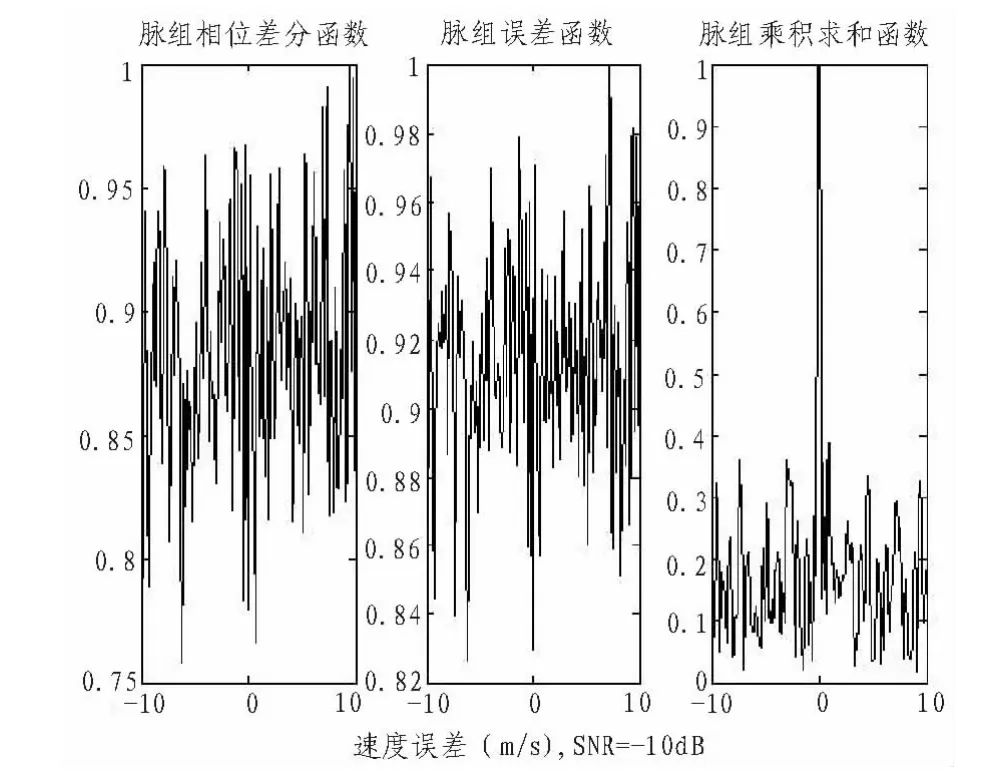
图2 三种精确速度搜索法的抗噪性能比较Fig.2 The anti-noise performance comparison of three kinds precise speed search method
由图可知采用最大脉组乘积求和法的速度估计精度非常高,在同样条件下SNR=-10dB时依然可以得到很高的精度。因此,本文选取用最大脉组乘积求和法作为精确速度的搜素算法。
3 仿真结果与分析
3.1 改进后步进频率的成像效果仿真分析
假设改进后的步进频率信号的参数为:中心频率f0=94 GHz,频率步进量△f=4 GHz,脉冲脉宽 T=0.1 μs,第一次脉冲重复周期Tr0=13 μs,帧周期脉冲积累数 N=128。假设目标匀速运动,三个散射点分别顺序相距5 m,归一化散射点强度之比为3:5:2。第一个强散射点距离雷达的径向距离为5 km。为了更好地评估改进后的信号的性能,假设在传播过程中存在噪声,回波信噪比为5 dB。为了使距离像的细节更清楚,采用补零的方法增加逆傅立叶变换点数提高采样分辨率,在文中采用补零到256点的方法以使距离像细化。
当目标静止时采用常规步进频率信号成像的结果如图3所示,以此为参考标准进行比较分析。当目标速度为1 500 m/s时,目标一维距离像的结果如图5所示,其中图4(a)表示用常规步进频信号直接成像的结果,图4(b)表示采用改进后步进频率信号成像结果。由图可知常规步进频率信号的一维距离像在最大不模糊距离窗内3个散射点大约都衰减50%,三个散射点波形发生展宽,峰值下降,导致距离分辨率大大降低,一维距离像产生失真。而改进后的步进频率信号的一维距离像只发生了平移,并没有产生失真,成像位置准确。

图3 目标静止v=0 m/s时一维距离像Fig.3 One dimensional range profile of target stationary v=0 m/s
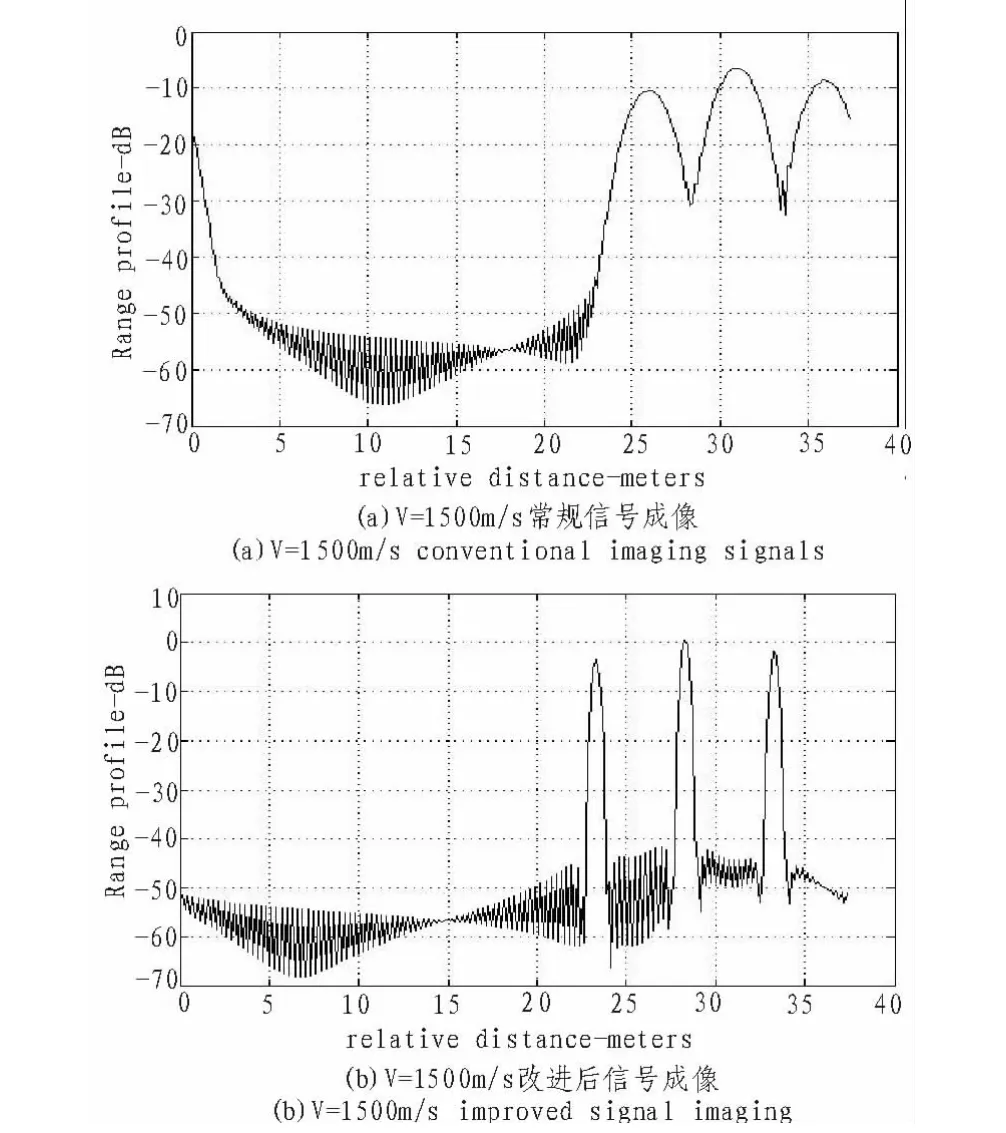
图4 v=1500 m/s时常规、改进后信号成像比较Fig.4 The profile comparison conventional and improved signal v=1500 m/s
3.2 速度补偿后成像效果仿真分析
当V=1 500 m/s时,采用文中提出的方法进行速度补偿,经过两次速度测量并补偿后得到的距离像成像准确,均能准确的反映出目标的散射点强度分布。图5(a)是补偿后的常规步进信号的距离像,由图可知补偿后常规信号的距离像峰值提高大约7个dB,波形展宽、距离分辨率下降、距离像失真等问题都得到了明显的改善,成像位置准确。图5(b)是改进后的频率步进信号补偿后的距离像,由图可知补偿后的成像位置得到准确补偿,经过补偿后的距离像与目标静止时得到距离像一致。
3.3 抗噪性能仿真结果分析
为检验文中提出方法的精确性,文中采取Monte-Carlo仿真试验方法进行验证,选取直接使用最大脉组乘积求和法进行对比,100次Monte-Carlo试验结果的均方值误差(RMSE)结果如图6所示。由图6可知,在低时域信噪比的情况下,采用本文提出的方法比直接使用最大脉组乘积求和法的估计精度要高,本文方法在信噪比为-4dB的时候仍能较准确地搜索到结果,但是直接使用时要在0dB以上才会得到准确的搜索结果,可知此方法抗噪性能也具有一定的优越性。

图5 v=1500 m/s时常规、改进信号补偿后的距离像比较Fig.5 The profile comparison conventional and improved signal after compensation v=1500 m/s

图6 与最大脉组乘积求和法性能对比Fig.6 The performance comparison for maximum burst multiplication summation
4 结论
综上所述,改进后的步进频率信号可以消除运动目标回波中二次附加相位项的影响,因此目标的一维距离像只发生距离走动并不会产生失真。经过使用互相关FFT测速法求粗速度和利用最大脉组求和准则搜索精确速度,仿真实验证明,此方法测速精度高,抗噪性能好,便于雷达接收系统进行实时处理,具有较好的工程应用价值。
[1]吴振凯.调频步进信号回波的速度补偿 [J].制导与引信,2010,31(1):37-42.
WU Zhen-kai.The velocity compensation of echo of linear modulated frequency-stepped signal[J].Guidance&Fuze,2010,31(1):37-42.
[2]孙慧霞,刘 峥,曹运合.高速运动环境下的调频步进信号运动参数估计[J].西安电子科技大学学报,2011,38(1):136-141.
SUI Hui-xia,LIU Zheng,CAO Yun-he.Estimation of a highvelocity targetpsmotion parameters for amodulated frequency stepped radar[J].Journal of Xidian University,2011,318(1):136-141.
[3]Chen H Y,Liu Y X,jiang W D,etal.A new approach for synthesizing the range profile of moving targets via steppedfrequencywaveforms [J].IEEE Geoscienceand Remote Sensing Letters,2006,3(3):406-409.
[4]林 云,司锡才.基于评价函数的步进频率信号速度补偿研究[J].航空兵器,2009,3:31-36.
LIN Yun,SI Xi-cai.Velocity compensation of steppedfrequency signal based on evaluation function [J].Aero Weaponry,2009,3:31-36.
[5]王桂丽,李兴国.频率步进和脉冲多普勒复合测速研究[J].红外与毫米波学报,2008,27(3):190-193.
WANG Gui-li,LI Xing-guo.Compound approach of measuring velocity base on step-frequency and pulse doppler system[J].Journal of Infrared and Millimeter Waves,2008,27(3):190-193.
[6]田进军,刘林,薛明华.一种频率步进雷达目标径向速度估计方法[J].北京航空航天大学学报,2008,34(6):673-675.
TIAN Jin-jun,LIU Lin,XUE Ming-hua.New estimation method of targets radial velocity for stepped-frequency radar[J].JournalofBeihang University ofAeronauticsand Astronautics,2008,34(6):673-675.
[7]肇格,胡杰民,张军.目标复杂运动对SFR一维距离成像影响分析[J].雷达科学与技术,2012,10(4):431-434.
ZHAO Ge,HU Jie-min,ZHANG Jun.Effects of Target Complex Motion on High Resolution Range Profile via SFR[J].Radar Science and Technology,2012,10(4):431-434.
[8]蔡飞,樊世杰,范红旗,等.一种逆V频率步进雷达的速度估计方法[J].雷达科学与技术,2011,9(1):244-247.
CAI Fei,FAN Shi-jie,FAN Hong-qi,etal.A novel velocity estimation method of inverse V-shape stepped-frequency radar[J].Radar Science and Technology,2011,9(1):244-247.
Study of a modified stepped-frequency radar signal and motion compensation
DUAN Hong1,2,WANG Xia1, WANG Meng-jun1
(1.School of Information,Hebei University of Technology,Tianjin 300401,China;2.63813Unit,Wenchang 571300,China)
A precise velocity estimation method is presented to solve range profile distortion and motion compensation from stepped-frequency radar.Firstly,the principle of the i-mproved and processed of stepped-frequency signal is expounded.which is the method of using cross correlate-on FFT velocimetry to estimate the target velocity roughly.Then the precise velocity is searched by the rule of the maximum burst multiplication summation.Finally,the speed compensation of the moving target are achieved to get preciseone dimensional range profile.The simulation results prove that accurate result is still got when S-NR is 4dB,the performance of improved signal is obviously improved and the one dimensional range profile is distortionless with target motion.So the method has high-precision and advantages of anti-noise.
stepped-frequency;one dimensional range profile;motion compensation;correlation function;maximum burst multiplication summation
TN92
A
1674-6236(2014)13-0136-04
2013-09-23 稿件编号:201309166
段 宏(1986—),男,云南大理人,硕士研究生。研究方向:数字信号处理。
