考虑摩擦的剪切损伤本构关系的力学分析
2014-09-22张治国刘丽丽
崔 崧, 张治国, 刘丽丽
(沈阳师范大学 物理科学与技术学院, 沈阳 110034)
考虑摩擦的剪切损伤本构关系的力学分析
崔 崧, 张治国, 刘丽丽
(沈阳师范大学 物理科学与技术学院, 沈阳 110034)
脆性和准脆性材料在外部载荷作用下,通常会表现出复杂的应力应变关系。其中,受压剪作用的裂纹是否摩擦滑动,对材料的剪切本构关系会产生很大的影响。之前在一些文献中提出过这种考虑裂纹摩擦效应的损伤本构模型,但只是理论假设,并没有进行过严格的证明。可以考虑一个受压剪作用的单元体,其中心含一条微裂纹,利用弹性力学理论中的复变函数方法可以给出单元体边界及裂纹所在平面处的位移场,通过某种平均化的方法,可得到单元体基体平均剪应变的一种形式,而这种形式与单元体边界及裂纹的几何尺寸有关,进一步可定义与这些几何尺寸相关的剪切损伤变量,将基体平均剪应变代入到弹性剪切本构关系中,可得到考虑摩擦效应的脆性和准脆性材料弹性剪切损伤本构关系。这种方法利用了现有的弹性力学理论,所以得到的结论是可靠的。
摩擦; 剪切; 弹性力学; 损伤; 本构关系
0 引 言
为了描述脆性和准脆性材料的复杂力学行为,采用唯象的各向异性损伤理论是一种比较有效的方法,而且有很多学者作了大量的相应工作[1-11]。对于受压剪作用的裂纹面,为了描述摩擦效应,Dragon等人[11]在损伤本构关系中引入一个二阶滑动张量γ,但模型较为复杂,为此文献[12]提出了一种简单实用的摩擦塑性损伤耦合模型,并作了一些应用[13]。
为了验证文献[12]的结论,可以考虑一个远端受压剪作用且中心含一条裂纹的薄板,在裂纹周围截取一单元体,对之进行弹性力学分析,可得到基体平均剪应变的表达式,再利用弹性剪切本构关系,则得到单元体的弹性剪切损伤本构方程,方程中的剪切损伤变量与单元体边界及裂纹尺寸有关。通过这种力学分析,证明了文献[12]有关摩擦的剪切损伤本构模型是正确的。
1 远端受压剪薄板内部的位移场
在文献[12]中考虑了一个平面问题下损伤主轴坐标系中受压剪作用的代表性体积单元,如图1所示。假设水平裂纹对应的剪切损伤变量ω12保持不变,作用在裂纹上的压力σn也恒定,则裂纹面上的最大摩擦力τf=μsσn,其中μs为材料的摩擦系数。文献[12]认为,当施加在单元上的剪应力τ12逐渐增加时,其剪切应力应变关系应为

图1 含一条裂纹的单元
下面用弹性力学理论来证明这个公式。考虑一个内部含一条裂隙的无限大薄板,如图2所示,裂隙沿x方向,长度为2a,远端受均布压剪载荷作用,其中均布剪力q1平行和垂直于x方向,均布压应力q2平行于y方向。
假设均布压应力q2不变,均布剪力q1由小到大逐渐增加,且加载依次分为2个阶段:1)当q1较小时,裂纹闭合且不滑动,裂纹面上承受与远端相同的剪力q1,薄板相当于无损状态;2)当q1增大到等于裂纹面能承受的最大剪应力τf=μsq2时,裂纹面开始滑动,薄板处于损伤状态,而裂纹面上的剪应力保持τf=μsq2不变。2个阶段裂纹面上承受的压应力保持q2不变。
我们知道,平面应力下薄板的位移分量的复变函数表示式为[14-15]
式中:E为材料杨氏模量;μ为泊松比;φ1(z)、ψ1(z)为变量z=x+iy的复变函数,若已知其表达式,代入上式中并将右边的实部和虚部分开,便可得到材料内任一点(x,y)的位移分量u和v。
对于加载的第1阶段,薄板远端和裂纹面分别受剪力q1、压应力q2的作用,4种边界条件各有其复变函数φ1(z)、ψ1(z)的表达式[14],其叠加形式为
其中,q2为负,q1为正。代入式(2),可得第1阶段薄板各点位移为
在加载的第2阶段,薄板远端受剪力q1、压应力q2的作用,裂纹面上承受剪力τf和压应力q2,4种边界条件下的复变函数φ1(z)、ψ1(z)的形式分别为
将式(4),式(5)代入式(2),可得到裂纹发生摩擦滑动时薄板各点的位移。
2 含裂纹单元体剪切本构关系的推导
在图2中薄板的裂纹周围截取一块单元体,如图3所示,裂纹对称位于单元体中央,单元体长度为2l,高度为2h,单元体受压剪作用,与图1中的研究对象类似。

图2 远端受压剪载荷的薄板

图3 中心含裂纹的单元体
在加载的第1阶段,薄板各点处剪应变γ12利用式(3)求出为

其中,G为剪切模量,且G=E/2(1+μ)。单元体的平均剪应变与上式相同,单元体的应力应变关系为
形式与式(1)中第1式是一致的。
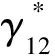


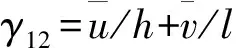

其中,f1,f2仅与单元体边界和裂纹的几何尺寸有关,与载荷大小无关,具体形式可见文献[16]。
对于裂纹面(y=0)上的位移u,由式(4)、式(5)和式(2)可得
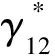

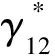
式(11)的形式与式(1)中的第2式是一致的。通过对两个加载阶段的力学分析得到公式(6)和式(11),我们就证明了式(1)是正确的。以上的分析是在平面应力条件下进行的,但结论同样适用于平面应变条件。
3 结 论
利用弹性力学理论对裂纹受压剪时的剪切弹性损伤本构关系进行了分析,得到的结论适用于脆性和准脆性材料,这是由于这种材料从加载到破坏过程中被认为一直是弹性的。该方法不仅可以分析剪切损伤本构关系的裂纹摩擦效应,也可以分析复杂载荷下拉伸和压缩损伤本构关系的裂纹摩擦效应,进一步可分析得到含随机裂纹材料的考虑摩擦效应的各项力学性能。
[ 1 ]KRAJCINOVIC D,FONSEKA G U. The continuous damage theory of brittle materials[J]. J Appl Mech, 1981,48(4):809-824.
[ 2 ]CHOW C L,WANG June. An anisotropic theory of elasticity for continuum damage mechanics[J]. Int J Fract, 1987,33(1):3-16.
[ 3 ]余天庆,钱济成. 损伤理论及其应用[M]. 北京:国防工业出版社,1993.
[ 4 ]SWOBODA G,SHEN Xinpu, ROSAS L. Damage model for jointed rock mass and its application to tunnelling[J]. Comput Geotec ,1998,22(3/4):183-203.
[ 5 ]SWOBODA G,YANG Qiang. An energy-based damage model of geomaterials (part 1 and part 2)[J]. Int J Sol S, 1999,36(12):1719-1755.
[ 6 ]KUHL E,RAMM E, BORST R. An anisotropic gradient damage model for quasi-brittle materials[J]. Comput Meth, 2000,183(1):87-103.
[ 7 ]冯西桥. 脆性材料的细观损伤理论和损伤结构的安定分析[D]. 北京:清华大学, 1995.
[ 8 ]余寿文,冯西桥. 损伤力学[M]. 北京:清华大学出版社, 1997.
[ 9 ]BASISTA M,GROSS D. The sliding crack model of brittle deformation: an internal variable approach[J]. Int J Sol S, 1998,35(5):487-509.
[10]HALM D,DRAGON A. An anisotropic model of damage and frictional sliding for brittle materials[J]. Euro J Mec A, 1998,17(3):439-460.
[11]DRAGON A, HALM D,DESOYER T. Anisotropic damage in quasi-brittle solids: modeling, computational issues and applications[J]. Comput Meth, 2000,183(3/4):331-352.
[12]崔崧,黄宝宗,张凤鹏. 准脆性材料的弹塑性损伤耦合模型[J]. 岩石力学与工程学报, 2004,23(19):3221-3225.
[13]崔崧,张锴,吕嫣,等. 复合材料层板非线性全耦合分析[J]. 沈阳师范大学学报:自然科学版, 2009,27(2):178-180.
[14]徐芝纶. 弹性力学:上册[M]. 4版. 北京:高等教育出版社, 2006.
[15]陆明万,罗学富. 弹性理论基础:下册[M]. 2版. 北京:清华大学出版社, 2001.
[16]崔崧,陈岚峰. 剪切损伤细观机理的弹性力学分析[J]. 沈阳师范大学学报:自然科学版, 2013,31(1):21-24.
Mechanicsanalysisofsheardamageconstitutiverelationwithfriction
CUISong,ZHANGZhiguo,LIULili
(College of Physical Science and Technology, Shenyang Normal University, Shenyang 110034,China)
The stress-strain relation of brittle and quasi-brittle materials is usually very complex under the external load. In compression shearing, the crack surface of materials may slide relatively, which can make a great influence to shear constitutive relation. In some of the existing literature, the friction effect has been considered, but the related constitutive equations have not been rigorously proved, only as a hypothesis. Considering a volume element with one micro crack, and using the method of function of the complex variable based on the theory of the elasticity, the displacement field of the boundary and the crack surface is analyzed. It can be got a form of the matrix average shear strain which related to the geometry of the element and the crack by some averaging method, further can define the shear damage variable associated with the geometry. By putting the matrix average shear strain into the elastic shear constitutive relation, the elastic shear damage constitutive relation with friction for brittle and quasi-brittle materials can be obtained. This method has applied the theory of the elasticity, so the result would be reliable.
friction; shear; elasticity; damage; constitutive relation
2014-08-18。
辽宁省教育厅科学研究项目(L2014442)。
崔 崧(1969-),男(满族),辽宁本溪人,沈阳师范大学副教授,博士。
1673-5862(2014)04-0553-04
O346.5
: A
10.3969/ j.issn.1673-5862.2014.04.021
