副高外围对流雨带中的对流—对称不稳定及锋生的诊断分析

王宗敏 丁一汇张迎新田利庆李江波

1南京信息工程大学大气科学学院，南京210044

2国家气候中心，北京100081

3河北省气象台，石家庄050021

1 引言

华北暴雨中，重要的一类是副高外围暴雨，它们是由西太平洋副热带高压（简称副高）与西来冷空气（常伴有西风槽）相互作用造成的。例如，在北京地区，这类暴雨占该地区大降水的46%（刘还珠等，2007）。

副高外围暴雨在卫星云图上的典型特点是，副高控制地区基本为晴空区，副高西北侧存在宽广的带状中低云区，在晴空区和低云区交界处常常产生间断的对流云带，云带上的对流单体常能达到MCC（mesoscale convective complex，中尺度对流复合体）的标准，有时它们能够合并形成连续的带状对流云系。在实际天气预报业务中，预报员常常把586或588 dagpm等高线作为副高外围的标志线，一般预报暴雨发生在这两条等高线之间。

由于副高外围对流降水的带状特征，容易使人联想到与带状云和降水相关的不稳定机制，如对称不稳定、惯性不稳定、重力波、Kelvin-Helmholtz不稳定等，另外锋生也可以造成带状云和降水（Schultz and Knox，2007）。那么，到底是哪一种或几种机制在副高外围对流云带中起主要作用？本文将从2009年8月25日发生的一个副高外围暴雨典型个例入手，对该问题进行分析。

首先分析这次暴雨发生、发展过程的云图特征，然后对此次过程进行模拟，在模拟较成功的基础上，利用模拟结果对其发生发展中的对流不稳定、对称不稳定、惯性不稳定、锋生等进行分析，最后给出分析结果。

2 副高外围对流云带发生发展过程的云图特征

2009年8月25日00时～26日00时（协调世界时，下同），河北中部到山西中南部出现大范围降水，尤其在河北中部有 10个乡镇雨量站降水超过100 mm，石家庄藁城的兴安镇雨量达149.1 mm。

25日00～08时，副高外围584 dagpm等高线的西北侧为宽广的带状中低云系，降水稀少，其东南侧华北南部受副高控制，为晴空区。从 09时开始，在584和588 dagpm等高线之间，共有4个对流云团发展，并排列成为线状（图1）。

09时，在山西、陕西交界处（37°N，110°E），第一个对流云团开始发展（图1中矩形区，将其标记为云团A），最低TBB达－70 °C。

12时，云团 A向东北方向移至山西中部（移向与500 hPa风一致），且达到Maddox规定的MCC标准（Maddox，1980），TBB低于－32 °C的冷云盖面积达1×105km2，TBB低于－52 °C的冷云盖面积达 5×104km2，但最低 TBB有所升高，为－62 °C。同时，在584和588 dagpm等高线之间有3个中 β尺度对流云团开始发展（见图 1中圆圈区、五角形区、圆角矩形区，标记为云团B、C、D）；黄河上游附近局地对流维持。一个有组织的对流云带清晰地显现出来。

18时，云团A向东偏北方向移动至河北东部，强度、面积均变化不大，最低TBB为－61 °C。对流云团B发展成为一个MCC，开始在山西南部产生降水。对流云团C有所发展。长江上游地区对流云团D也发展成为一个MCC。

21时，对流云团A、B和C都开始减弱。长江上游地区的对流云团D发展到成熟阶段。

对流云团A从25日09时开始发展，达到MCC标准后，于21时开始减弱，生命史约为12 h。对流云团B、C的生命史约为9 h。这3个对流云团的移动方向均为偏东，但云团A移动较快，云团B、C移动较慢，云团A、B、C的移速近似为500 hPa上风速。云团D的生命史最长，且基本在原地发展，没有移动。

虽然本次过程在华北暴雨中不算最强，但其代表了华北汛期副高外围西南气流与西来弱冷空气相互作用产生的一类典型暴雨过程。这类暴雨是由一条对流雨带直接造成的。对流雨带由若干具有一定间隔的中尺度对流单体组成，单体在随对流层中层（500 hPa）环境气流的移动中逐渐发展直至消亡。对流雨带的西北侧为宽广的带状斜压云系，降水较弱，东南侧为副高控制区，基本为晴空区。类似的暴雨个例还有2005年8月16日、2008年7月14日、2008年8月10日、2009年9月4日等。

3 暴雨过程的模拟

常规探空资料和NCEP再分析资料（1°×1°，6 h间隔）难以再现这个对流雨带的发生发展过程。为了再现对流雨带的发生发展过程，并分析产生对流雨带的不稳定条件，本文利用WRF中尺度数值预报模式对这次暴雨过程进行了模拟。

3.1 模式说明

采用WRF模式V3.3版本（2011年4月发布），两层嵌套，区域选取如图2所示。外层区域（D1）格点数为 83×70，分辨率为 30 km；第二层区域（D2）格点数为162×123，分辨率为10 km。模式垂直分为27层。微物理过程采用Lin等的方案，长波辐射采用RRTM方案，短波辐射采用Dudhia方案，近地面层方案为MYJ Monin-Obukhov方案。模拟中，一个重要参数——重力波拖曳参数选为1，这样模式动力过程中就考虑了重力波的拖曳作用，这时外层区域地形分辨率取“10 min＋2 min”，第二层区域地形分辨率取30 s（约1 km）。

本次模拟采用NCEP FNLs分析资料作为中尺度模式的初始场和侧边界条件，资料分辨率为 1°×1°，时间间隔为6 h。为了避开spin-up时间窗，将模式积分的开始时间设在24日18时，模式积分30 h，这样保证了25日00时～26日00时预报场的协调性。

模式分辨率的选取基于以下考虑：从降雨的雷达回波来看，较强雨带宽度可达80 km，因此，采用 10 km分辨率的网格足够捕捉该雨带。另外，Persson and Warner（1991，1993）、Ducrocq（1993）研究发现，为了能捕捉对称不稳定产生的倾斜对流，水平分辨率最少应为15 km，最好为5～10 km，所以，这次模拟采用10 km分辨率的网格，应该能够捕捉对称不稳定产生的倾斜对流。

3.2 模拟结果分析

对比25日00时～26日00时24 h降水的实况和预报结果（图 3）可见：对于西北地区东部的降水（图3a、b中椭圆所示区域），模拟的量级较小，但雨带走向较一致；对于华北地区南部到东北地区南部的降水（图 3a、b中矩形所示区域），模拟的量级和走向都比较一致。由于海上观测资料缺乏，图 3a中渤海区域降水资料由插值处理而得，数值很小，不能完全反映降水的真实情况，而模拟结果（图3b）则较合理地再现了此区域的降水分布。总体来看，降雨落区和强度的预报结果与实况较吻合。

为了分析对流雨带发展过程的模拟效果，图 4给出了25日12时、13时、16时、18时的卫星云图实况和对应时次的模拟的1 h降水量。可见，对于A、B、C三个对流云团，模拟的1 h降水量分布上均有反映，而且其走向和云带的走向较一致。所以，模式对对流雨带发展过程的模拟也比较理想。

从模拟的降水雷达回波来看，06时副高的西北侧边缘出现零散回波，09时对流开始发展，至 12时形成明显的带状结构，15时河北中部回波发展旺盛，而对流带前部的回波明显减弱，其发展过程与实况较吻合（图略）。

总之，模拟结果较好地再现了对流雨带的发生、发展过程，因此，可以利用模拟的高空、地面数据来分析其发生、发展的原因。

4 对流雨带发生发展中的对流—对称不稳定分析

4.1 对流—对称不稳定概念及分析方法简述

对流—对称不稳定，也就是对流、对称不稳定共存的一种不稳定，这种情况在大气中可以经常见到（Jascourt et al., 1988；Reuter and Yau, 1993；Lagouvardos and Kotroni, 1995；Martin，1998；边清河等，2006；程艳红和陆汉城，2006；杜楠等，2008；费建芳等，2009；王亦平等，2008）。Jascourt et al.（1988）首先称这种情况为对流—对称不稳定。由于对流—对称不稳定与对流动量输送以及科里奥利旋转有关，所以国内学者也称其为非线性对流—对称不稳定（陆汉城等，2002；寇正和陆汉城，2005）。

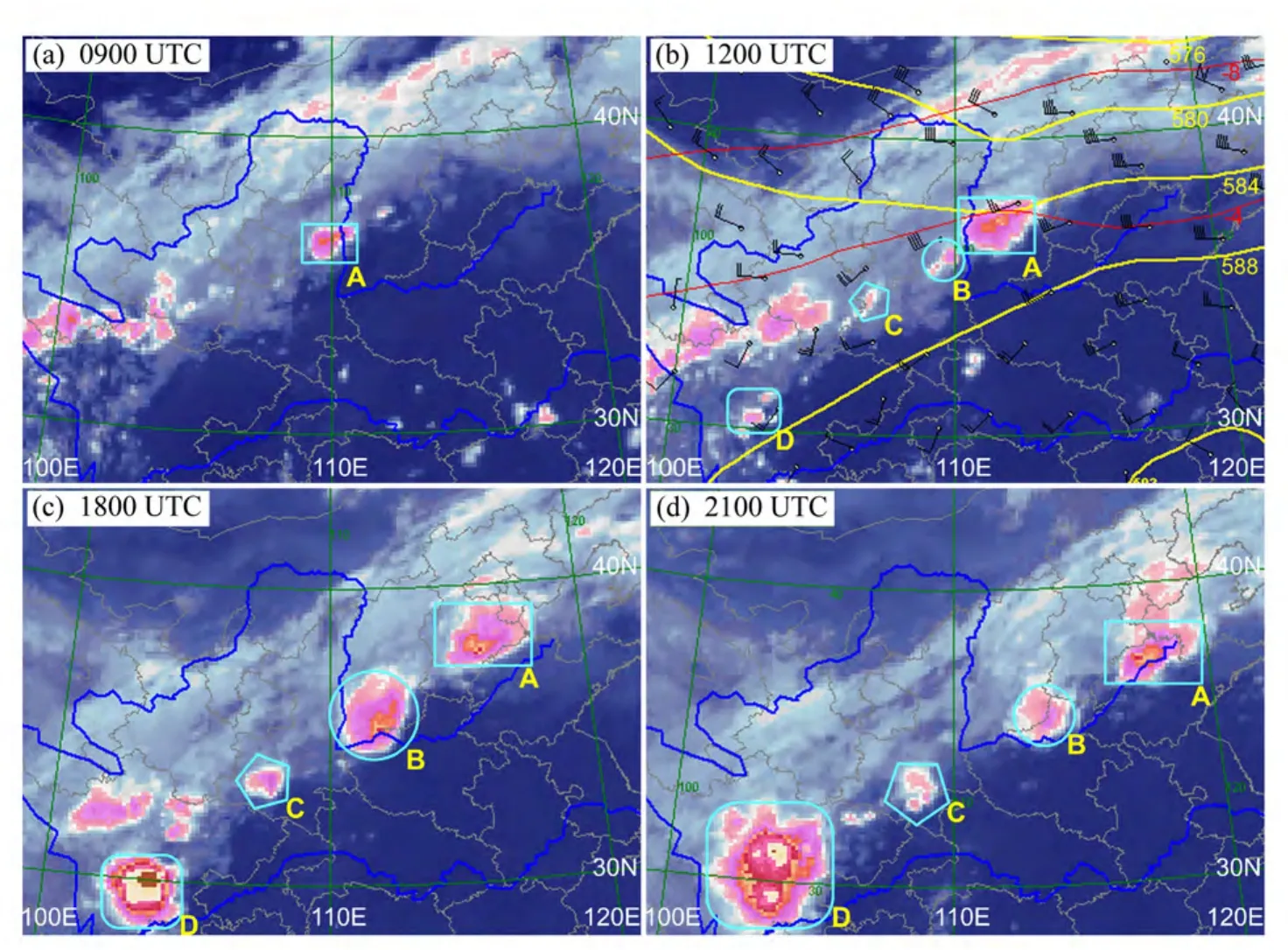
图1 2009年8月25日FY2-D静止卫星红外云图：（a）09时；（b）12时；（c）18时；（d）21时Fig.1 FY2-D stationary satellite infrared images on 25 August 2009: (a) 0900 UTC; (b) 1200 UTC; (c) 1800 UTC; (d) 2100 UTC

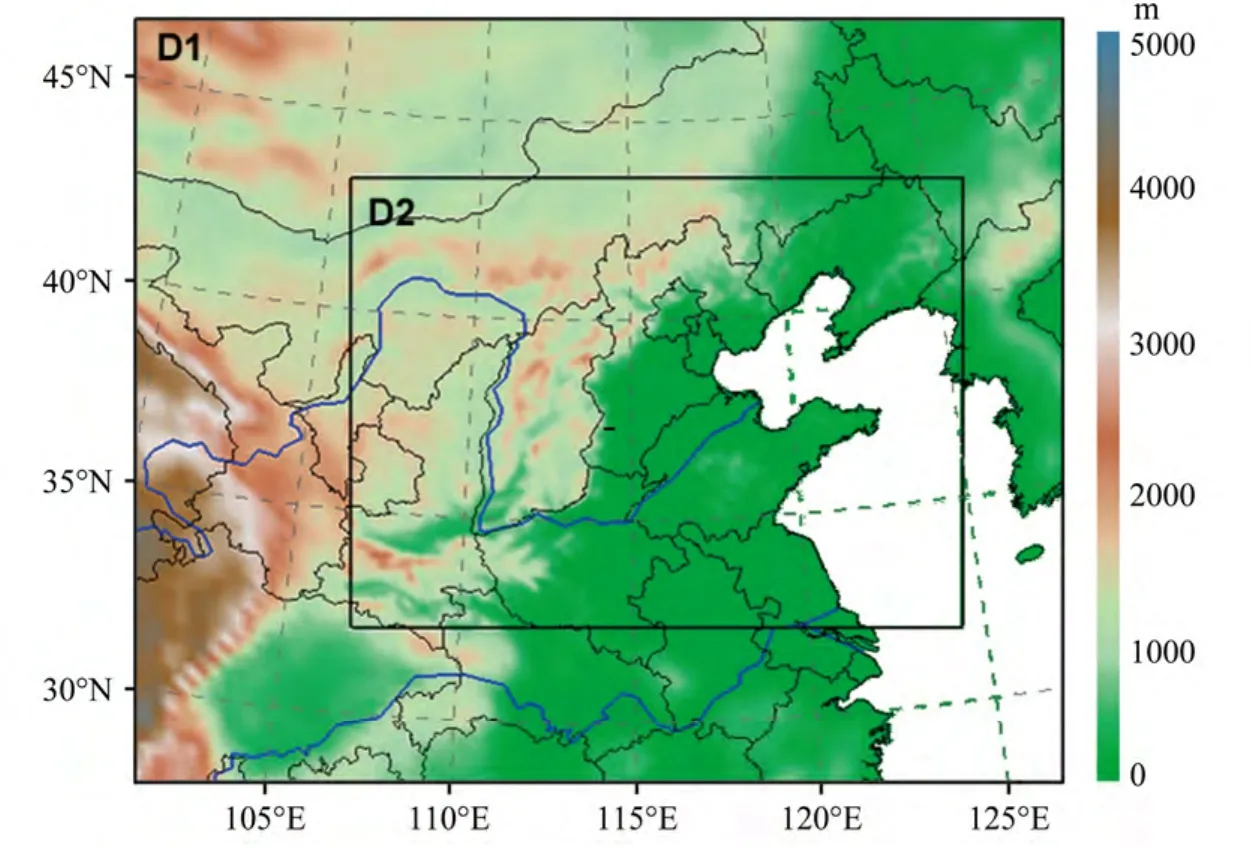
图2 模式区域设计。阴影表示地形高度Fig.2 Design of model domains.Shadings show the topography

Xu and Clark（1985）认为重力对流和倾斜对流是连续的统一体。然而，在初始条件稳定和湿对称稳定的斜压大气中，如果大气由于地面加热或地转风的垂直切变增大等因素变得不稳定，则湿对称不稳定将在条件不稳定产生之前出现，但是由于湿重力对流的增长率和能量释放比湿倾斜对流要大，所以，重力对流一旦产生，将很快占主导优势（Schultz and Schumacher，1999）。程艳红和陆汉城（2006）通过数值试验揭示了位势对称不稳定条件下重力对流的发展过程。

Xu（1986）提出了两种雨带形成机制，目前认为这两种机制是对流—对称不稳定的形式。第一种是“逆尺度发展型”（upscale development），其中小尺度的湿重力不稳定首先发展起来，随后，当环境呈重力稳定时，对称不稳定能量释放产生中尺度云带。这种类型的对流最有可能在锋区的外面产生。第二种是“降尺度发展型”（downscale development），在湿对称不稳定环境中，锋区内上升运动产生云，进而产生凝结潜热，凝结潜热使中层对流层不稳定，从而产生重力对流，最后由于湿重力不稳定能量的释放导致云带形成。Xu（1986）提出的“降尺度发展型”与Bennetts and Hoskins（1979）假设的锋区降水云带发展的3个阶段较相似。

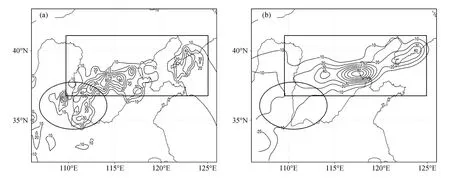
图3 2009年8月25日00时～26日00时24 h降水量（等值线，间隔：5 mm）（a）实况和（b）模拟结果。图3a中降水量格点数据由自动站资料通过Barnes客观分析方法插值得到Fig.3 (a) Observed and (b) simulated 24-h rainfall (isolines at 5 mm interval) from 0000 UTC 25 to 0000 UTC 26 August 2009.The gridded data in Fig.3a are created from AWSs point data by using the Barnes Objective Analysis in Integrated Data Viewer (IDV)

对流—对称不稳定的分析包括对流不稳定和对称不稳定的分析。对流不稳定用∂θe∂p分析。对称不稳定的分析方法有位涡分析法、Mg−θ(θe,垂直剖面图法、倾斜对流有效位能（SCAPE）法、Richardson数、增长率法等（丁一汇和沈新勇，1994；Schultz and Schumacher，1999；费建芳等，2009）。本文分别用位涡分析法、Mg−θ(θe)垂直剖面图法和Richardson数来分析对称不稳定。

4.2 湿位涡分析

4.2.1 湿位涡分析方法

对称不稳定的位涡分析方法是Mg−θ(θe,关系法在三维方向的扩展（Hoskins, 1974）。地转位涡 PVg=gηg·∇θ。其中：g为重力加速度；ηg为三维地转绝对涡度；∇为三维梯度算子。在惯性稳定、干重力稳定条件下，干对称不稳定（symmetric instability，SI）的存在条件是PVg＜0。类似地，在大气为惯性稳定和条件性稳定的情况下，条件性对称不稳定（conditional symmetric instability，CSI）的存在条件是 MPgηg·∇＜0；在大气为惯性稳定和位势稳定（也称对流性稳定）的情况下，位势对称不稳定（potential symmetric instability，PSI）的存在条件是 MPVg=gηg·∇θe＜0。在大气饱和或接近饱和的情况下，因为e，所以MP=MPVg。条件性对称不稳定和位势对称不稳定统称为湿对称不稳定（moist symmetric instability，MSI）。

以位涡（ PVg、 MP、 MPVg）分析计算对称不稳定的主要优点是三维的，且不受Mg−θ(θe,关系图的假定条件限制，是一种常用的客观定量分析对称不稳定的有效方法。

在实际分析时，常用湿位涡(moist potential vorticity，MPV)来代替 MPVg。 MPV =gη·∇θe。其中：η为三维绝对涡度，用全风速计算（Gray and Thorpe，2001；Clark et al.，2002；Jurewicz and Evans，2004；Novak et al.，2004，2006；边清河等，2006；王亦平等，2008）。之所以用全风速代替地转风，是因为中尺度模式模拟的地转风常包含更多的噪音（noise）。

本文用湿位涡MPV结合对流稳定度（∂θe∂p）和惯性稳定度（绝对涡度，即ςa=ς+f）来分析对流发生、发展时刻的对称不稳定情况。

4.2.2 对流—对称不稳定的水平分布

图5为25日08时和09时750 hPa上MPV、

对流稳定度、惯性稳定度的水平分布。可以看到，08时和09时存在两个明显的雨带，北侧雨带回波较弱且为连续雨带，南侧雨带为副高外围的对流雨带，整体呈带状，但为间断性雨带，表现为对流性降水。与北侧雨带对应的是一个惯性不稳定区域（ςa＜0）。副高外围对流雨带位于对流性稳定（ ∂θe∂p＜0）和对流性不稳定（ ∂θe∂p＞0）的过渡区。在其西北侧，则为明显的对称不稳定区（MPV＜0，同时∂θe∂p＜0，ςa＞0，即图中标识为MSI区域）。在副高外围对流雨带东南侧的副高控制地区，为大范围的对流不稳定区。

图4 25日（a）12时、（b）13时、（c）16时和（d）18时FY2-D静止卫星红外云图（彩图）和模拟的对应时次1 h降水量（灰色阴影，单位：mm）Fig.4 FY2-D stationary satellite infrared images (color shadings) at (a) 1200 UTC, (b) 1300 UTC, (c) 1600 UTC,and (d) 1800 UTC on 25 August 2009 and simulated 1 h rainfall (grey shadings, units: mm) at the same times

图5 模拟的8月25日08时（a）、09时（b）750 hPa上负MPV（MPV＜0，灰色阴影，单位：PVU；1 PVU＝1×10–6 K m2 kg–1 s–1）、正的∂θe∂p（ ∂θe∂p＞ 0，红色实线，间隔：2×10–2 K hPa–1）、负绝对涡度（ ＜0，黑色虚线，间隔为0.5×10–5 s–1）以及组合反射率（彩色阴影，单位：dBZ）。直线BE表示垂直剖面的位置Fig.5 Simulated negative MPV (MPV＜0, grey shadings,units: PVU; 1 PVU=1×10-6 K m2 kg–1 s–1), positive∂θe∂p(∂θe∂p＞ 0, red solid lines at 2×10–2 K hPa–1 interval), negative absolute vorticity (ςa＜0, black dashed lines at 0.5×10–5 s–1 interval), and composite reflectivity (color shadings, units:dBZ) at 750 hPa at (a) 0800 UTC and (b) 0900 UTC on 25 August 2009.The straight line BE identifies the location of vertical cross section

4.2.3 对流—对称不稳定的垂直分布

图6、7分别给出了08时、09时沿与锋区垂直的直线B（40°N，109.8°E）－E（37.3°N，111.4°E），所做的垂直速度、MPV、对流稳定度和惯性稳定度的垂直剖面。

08时（对流发生时），由图6a可见，距离B点250 km附近（对流09时在此处得到发展），从地面到400 hPa（8 km）之间，为0.1～0.2 m s–1的弱垂直上升区，这可能是大尺度辐合场造成的。距离B点200 km附近（对流发生处），从地面到600 hPa（4 km）之间，有一个弱倾斜上升区（垂直速度为0.1～0.2 m s–1），这可能是锋面抬升造成的。从此时的不稳定度（图6b）来看，在距离B点250 km附近（对流发展处），大气中低层为对流不稳定区，而在距离B点200 km附近（对流发生处）的弱倾斜上升区，700 hPa以下为对称不稳定区，700～500 hPa存在对流不稳定和弱的惯性不稳定。

09时（对流发展时），由图7a可见，距离B点250 km附近（对流发展处），从地面到600 hPa之间的上升区明显向冷区倾斜，垂直速度最大为 0.4 m s–1；而在600 hPa以上为垂直上升区，垂直速度在500 hPa达到1.2 m s–1。这说明对流层低层的垂直上升机制与中层以上有所不同。同时，在对流上升区的左侧，尤其是在700 hPa以下存在一个下沉区。从不稳定性的分布（图7b）来看，在距离B点250km附近，地面附近为对称不稳定和对流不稳定的交界。相对08时，09时700～500 hPa的对流不稳定度明显减弱，而惯性不稳定明显加强，这可能反映了惯性不稳定对对流带发生所起的作用，也可能是对流反馈的结果。

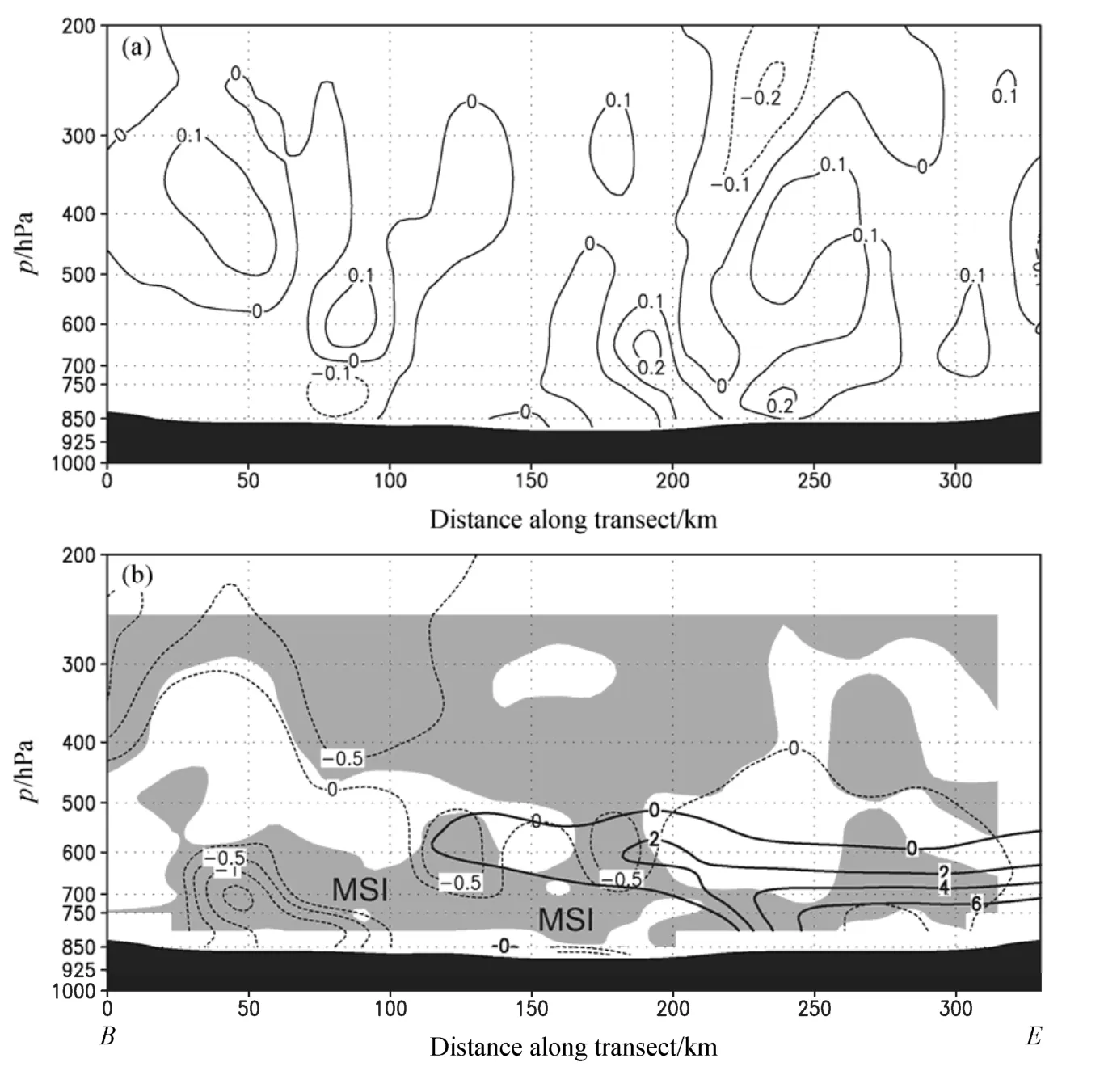
图6 模拟的25日08时垂直剖面（剖面位置见图5）：（a）垂直速度（间隔：0.1 m s–1）；（b）负MPV（阴影，单位：PVU）、正的∂θe∂p（实线，间隔：2×10–2 K hPa–1）和负绝对涡度（虚线，间隔：0.5×10–5 s–1）Fig.6 Simulated vertical cross sections(Location of the cross section is shown in Fig.5) at 0800 UTC 25 August 2009: (a) Vertical velocity (isolines at 0.1 m s–1 interval); (b) negative MPV (shadings, units: PVU), positive∂θe∂p(solid lines at 2×10–2 K hPa–1 interval), and negative absolute vorticity (dashed lines at 0.5×10–5 s–1 interval)

图7 同图5，但为25日09时Fig.7 Same as Fig.5, but for 0900 UTC 25 August 2009

综上所述，对流的发生、发展阶段都伴有对称不稳定、对流不稳定以及惯性不稳定的存在。发生阶段，在对流发生位置，对称不稳定分布在700 hPa以下，700～500 hPa存在对流不稳定和弱的惯性不稳定，此时存在弱的倾斜上升运动。在发展阶段，对流发展位置为对称不稳定和对流不稳定的交界处，700～500 hPa的对流不稳定度明显减弱，而惯性不稳定明显加强，此时低层为倾斜上升区，中高层为垂直上升区，对流的左侧对应下沉区，对流呈现明显的倾斜对流和垂直对流的混和特征，体现了对称不稳定和对流不稳定的共同作用。

4.3 M−θe 剖面

为了进一步说明对流发生发展过程中对称不稳定的存在，下面用Mg−θ(θ)垂直剖面图法来分析对称不稳定。

用Mg−θ(θe)剖面分析对称不稳定是一个直观、定性的方法。当等绝对地转动量（Mg）面的倾斜度小于等θ(θe)面时，空气块倾斜上升时就会产生对称不稳定。徐文慧等（2010）、蒙伟光等（2004）、Shou and Li（2008）通过沿某一经线做Mg−θ(θe剖面来判断对称不稳定的存在，其绝对地转动量的计算公式取为Mg=ug−fy。其中，Mg为西风绝对地转动量，ug地转风西风分量，y为垂直所取经线的距离。

本文用动量MVfy= − 代替Mg=Vg–fy。其中：V为沿锋区方向的风速；Vg为沿锋区方向的地转风速度；y为垂直锋区方向的距离。应该指出，这是一个近似的方法，之所以用V代替Vg，与前文计算MPV一样，也是因为中尺度模式模拟的地转风包含更多噪音的缘故。不过，因为V取沿锋区方向的风速，y取垂直锋区方向的距离，所以M同时包含了西风和南风的绝对动量，而不是仅仅计算了西风的绝对动量。

图 8给出了 08时沿与锋区垂直方向的直线B(40°N, 109.8°E)－E(37.3°N, 111.4°E)的M−θe剖面。可见，在750 hPa以下、距离B点170 km到230 km之间的区域（图8中黑色方框所示），以及850 hPa到650 hPa、距离B点25 km到75 km之间的区域（图8中灰色方框所示），等M面的倾斜度小于等θe面的倾斜度，表明存在明显的对称不稳定。在距离B点75 km到170 km之间，对流层低层等M面近似平行θe面的倾斜度，说明这里的对称不稳定不明显。从M−θe剖面图中分析得到的对称不稳定的分布基本对应图 5中对称不稳定的分布。

4.4 湿Richardson数

人们也常用Richardson数来判断对称不稳定的存在。根据对称不稳定的线性理论（丁一汇和沈新勇，1994），无限湿大气的对称不稳定的判据之一为湿理查森数（Ri*）小于某临界值，即：。其中：=(g/θ0)∂θw/∂z；θ0为大气基态位温。张可苏（1988）采用f平面内的非静力平衡滤声波模式，即非弹性假设，讨论了垂直方向有界的对称不稳定性，得到斜压基流对称不稳定的条件为：其中：fa=f−为涡度；n为垂直波数；L为水平方向的半波长；为热成风的惯性圆半径。在没有水平切变时，只有 0＜Ri＜1时，才有对称不稳定。刘子臣等（1997）、盛春岩和杨晓霞（2002）用作为对称不稳定的判据。

下面用湿Richardson数来进一步说明对称不稳定的存在。图9给出了08时沿与锋区垂直方向的直线BE（位置如图5所示）的湿理查森数剖面。湿理查森数的计算公式（刘健文等，2005）为：

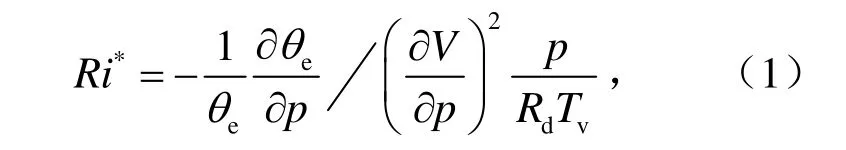
其中：V为风速，虚温Tv= (1 + 0.608q)T。考虑到比湿q的量级为10–4～10–3，vTT≈，故：

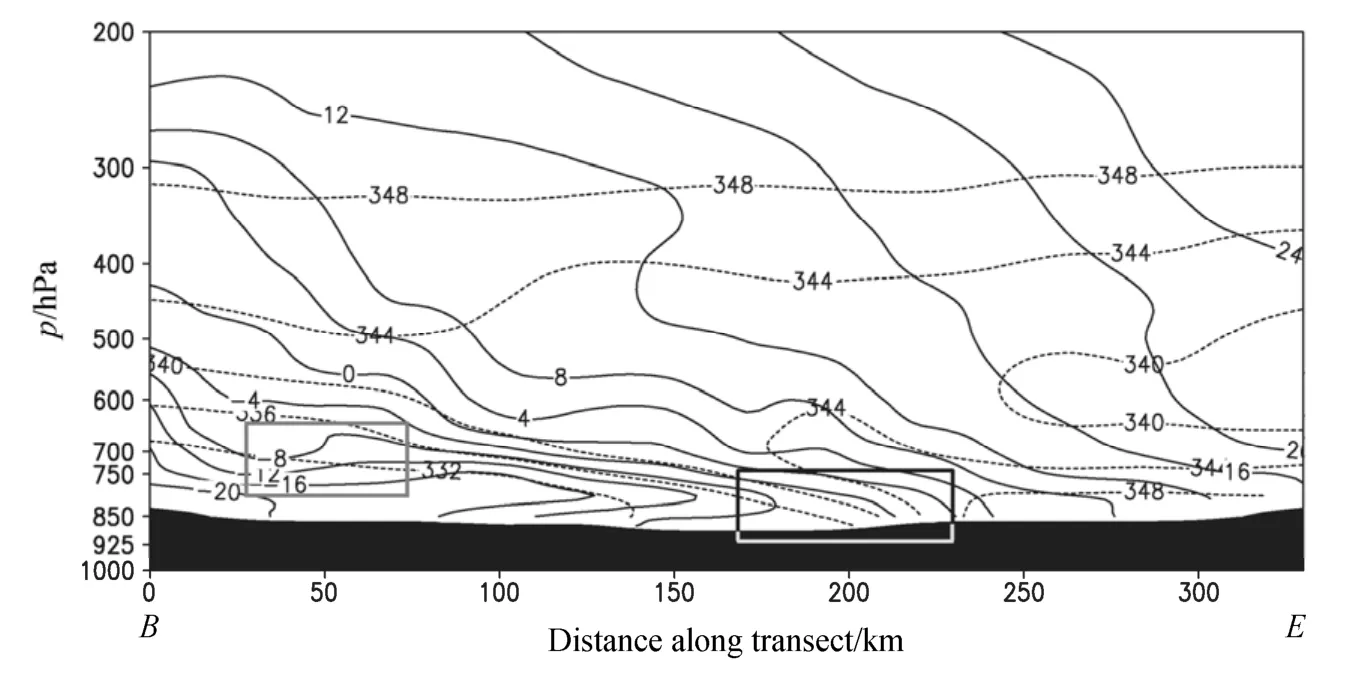
图8 模拟的25日08时M−θe的垂直剖面（剖面位置见图5）。动量M（实线，间隔：5 m s–1），θe（虚线，间隔：4 K）Fig.8 SimulatedM−θevertical cross sections(Location of the cross section is shown in Fig.5) at 0800 UTC 25 August 2009.M (solid lines at 5 m s–1 interval),θe(dashed lines at 4 K interval)

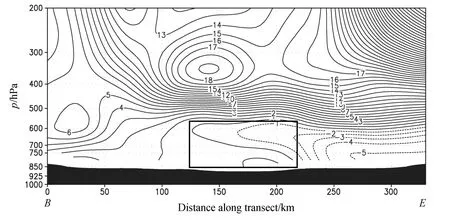
图9 模拟的25日08时Ri*（等值线，间隔为1）的垂直剖面（剖面位置见图5）Fig.9 Simulated vertical cross section ofRi*(isolines at 1 interval) at 0800 UTC 25 August 2009.Location of the cross section is shown in Fig.5

本文采用此式计算湿理查森数。

由图9可见，在水平距离B点125～220 km、垂直 850～600 hPa之间，即图中矩形所示的区域内，左下部湿理查森数*Ri小于1、大于0，表明存在对称不稳定，而此区域的右上部*Ri＜0，表明存在对流不稳定，故此矩形区域为对称不稳定和对流不稳定共存的区域。对流发生在距离B点200 km附近，所以，从*Ri来看，对流的发生是对称—对流不稳定作用的结果。

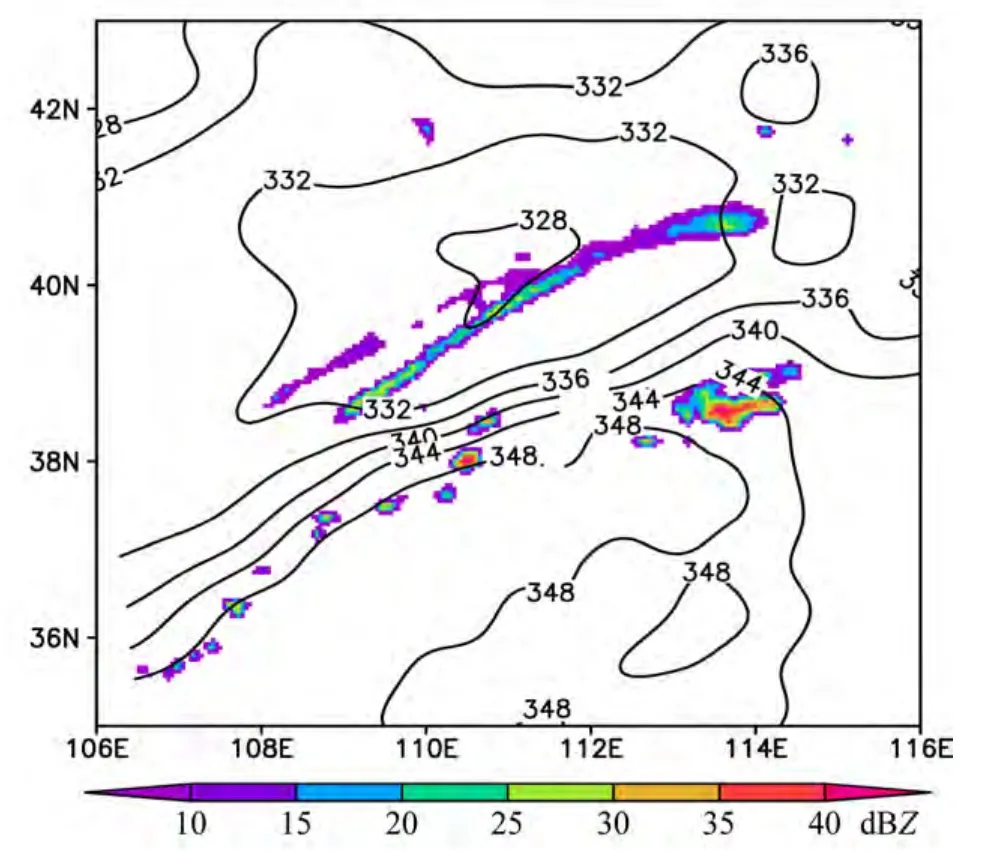
图10 08时800 hPa上eθ的水平分布（等值线，间隔为2 K）和组合反射率（阴影，单位：dBZ）Fig.10 Horizontal distribution ofeθ(isolines at 2 K interval) and composite reflectivity (shadings, units: dBZ) at 800 hPa at 0800 UTC 25 August 2009

5 锋生作用

对称不稳定的释放离不开锋生强迫。Fischer and Lalaurette（1995a，1995b）通过比较小扰动和有限振幅扰动（如锋生、地形环流等）两种情况下的增长率和垂直速度发现，外界强迫是MSI能否释放的一个重要条件。Schultz and Knox（2007）对发生在美国Montana州东部和南、北Dakolas州的一次带状降水个例进行了分析，认为产生带状降水的原因是在锋生的环境中对称不稳定的释放（也可能有惯性不稳定的作用）。王建中和丁一汇（1995）认为，在 1986年一次华北强降雪中，弱的对称不稳定和锋生强迫对华北东部的降雪同时起作用。

在本次过程中，对流带发生在锋区之中。图10给出了08时800 hPa上eθ的水平分布，可以看到，从西北地区东部到华北地区西部存在一个东北—西南向的锋区，在锋区的暖湿空气一侧有弱的降水回波出现。

沿与锋区垂直的方向做垂直剖面（图 11），可以发现，在锋区的前沿即干冷空气与暖湿空气交汇的地区（图11中方框所示），750 hPa以下存在强烈的锋生，最大值达到了 10 K (100 km)–1(3 h)–1，正是在该区域，09时开始产生了较强的倾斜—垂直混和对流。

锋生强迫能够克服湍流扩散和补偿下沉对对称不稳定能量释放的抑制作用，所以锋生的存在提供了对称不稳定能量释放的有利条件，从而也提供了对流—对称不稳定能量释放产生倾斜—垂直混和对流的有利条件。

本文锋生计算公式为：

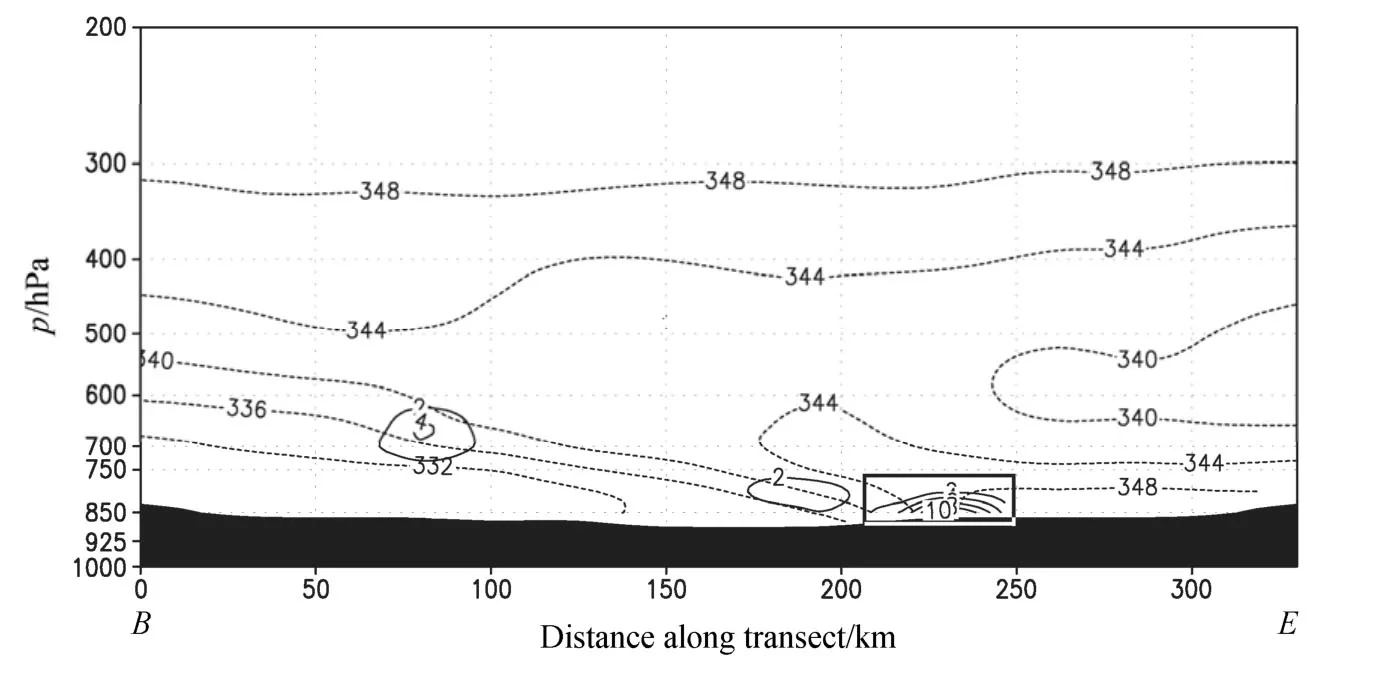
图11 08时eθ（虚线，间隔：2 K）、锋生［实线，间隔：2 K (100 km) –1 (3 h)–1］的垂直剖面（剖面位置见图5）Fig.11 Vertical cross sections of eθ(dashed lines at 2 K interval) and frontogenesis [solid lines at 2 K (100 km)–1 (3 h) –1 interval] at 0800 UTC 25 August 2009.Location of the cross section is shown in Fig.5

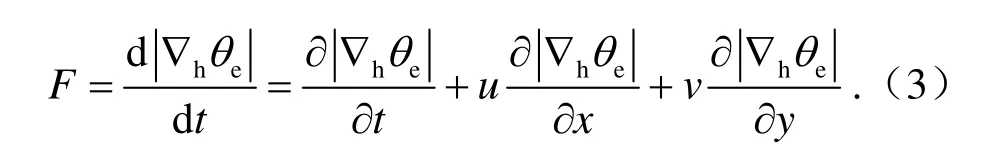
6 雨带的走向与对称不稳定

Seltzer et al.（1985）、Lagouvardos et al.（1993）详细列举了与对称不稳定相联系的带状降水特征，如雨带基本与热成风平行，且最强降水出现在不稳定区域，雨带随环境气流移动而不是传播，多雨带之间的距离与不稳定气层的厚度及等熵面的倾角有关，雨带中上升气流的倾斜面应位于等熵面与等Mg面之间等。

在此次过程中，对流雨带表现为单雨带，雨带与 500～800 hPa等厚度线即热成风基本平行，而与500 hPa等高线存在明显的交角（图12）。雨带中的对流单体随环境气流移动，并无传播现象。这些特征均符合与对称不稳定相联系的带状降水特征。

在实际预报业务中，预报员常用500 hPa上588或 584 dagpm等高线来确定副高外围对流雨带的走向。根据上述分析，这不符合对称不稳定的理论。根据与对称不稳定相联系的带状降水特征，500 hPa风可作为环境气流分析，而雨带的走向应该用等厚度线或热成风分析，也可以近似用高、低空（如500 hPa与800 hPa）之间的风切变来分析。

图12 25日09时500～800 hPa位势厚度（实线，间隔：10 gpm）、500 hPa位势高度（虚线，间隔：2 dagpm）以及组合反射率（阴影，单位：dBZ）Fig.12 The 500–800-hPa geopotential thickness (solid lines at 10 gpm interval), 500-hPa geopotential height (dashed lines at 2 dagpm interval),and composite reflectivity (shadings, units: dBZ) at 0900 UTC 25 August 2009

7 结论和讨论

通过对2009年8月25日副高外围对流雨带的模拟和分析，得到如下主要结论：

（1）副高外围对流雨带由若干具有一定间隔的中尺度对流单体组成，单体在随对流层中层（500 hPa）气流的移动中逐渐发展直至消亡。对流雨带的西北侧为宽广的带状斜压云系，降水较弱，东南侧为副高控制区，基本为晴空区。

（2）对流雨带发生在对流层低层（700 hPa以下）的对称不稳定区，700～500 hPa存在对流不稳定和弱的惯性不稳定。随着对流雨带的发展，700～500 hPa的对流不稳定度明显减弱，而惯性不稳定明显加强。

对流发展时刻，低层为倾斜上升区，中高层为垂直上升区，对流左侧对应下沉气流，对流呈现明显的倾斜对流和垂直对流的混和特征，体现了对称不稳定和对流不稳定的共同作用，即对流—对称不稳定的作用。

（3）M−θe剖面和湿理查森数的分析，进一步表明了副高外围对流雨带的中对流—对称不稳定的存在。

（4）锋生的存在提供了对称不稳定能量释放的有利条件，从而也提供了对流—对称不稳定能量释放产生倾斜—垂直混和对流的有利条件。

（5）此次副高外围对流雨带表现为单雨带，与500～800 hPa等厚度线即热成风基本平行，而与500 hPa等高线存在明显的交角。雨带中的对流单体随环境气流移动，而不是传播。雨带符合与对称不稳定相联系的带状降水特征。

上述结论对实际预报有一定指导意义。根据上述结论，预报副高外围的雨带位置，不仅需要考虑对流稳定性，更需要考虑对称稳定性以及锋生的位置，预报雨带的走向需要参考500～800 hPa等厚度线（热成风），而不是588 dagpm或其他等高线的走向。

本文虽然指出了副高外围对流为对流—对称不稳定的释放造成的倾斜、垂直对流的混和体，但由于模式输出的时间间隔为 1 h，并没有给出倾斜和垂直对流发展的详细过程，这需要缩小模式输出的时间间隔以便进一步分析。另外，副高外围对流雨带为什么是间断性的雨带，雨带上对流单体之间的距离是多少，以及如何合并等？这些问题需进一步深入探讨。

（References）

Bennetts D A, Hoskins B J.1979.Conditional symmetric instability—A possible explanation for frontal rainbands [J].Quart.J.Roy.Meteor.Soc.,105: 945–962.

边清河, 丁治英, 董金虎, 等.2006.“96.8” 华北暴雨数值模拟与稳定性分析 [J].气象, 32 (8): 17–22.Bian Qinghe, Ding Zhiying, Dong Jinhu, et al.2006.Numerical simulation for “96.8” Huabei heavy rain and its stability analysis [J].Meteorological Monthly (in Chinese), 32 (8):17–22.

程艳红, 陆汉城.2006.对流对称不稳定的发展演变和环流特征 [J].热带气象学报, 22 (3): 253–258.Cheng Yanhong, Lu Hancheng.2006.The evolution and circulation feature of convective-symmetric instability[J].Journal of Tropical Meteorology (in Chinese), 22 (3): 253–258.

Clark J H E, James R P, Grumm R H.2002.A reexamination of the mechanisms responsible for banded precipitation [J].Mon.Wea.Rev.,130: 3074–3086.

丁一汇, 沈新勇.1994.对称不稳定理论及其应用问题（一）线性理论 [J].应用气象学报, 5 (3): 361–368.Ding Yihui, Shen Xinyong.1994.A review of the symmetric instability theory and its application.Part Ⅰ:Linear theory [J].Journal of Applied Meteorological Science (in Chinese),5 (3): 361–368.

杜楠, 钟玮, 陆汉城, 等.2008.一次四川暴雨过程的非线性对流—对称不稳定分析 [J].南京气象学院学报, 31 (3): 308–316.Du Nan,Zhong Wei, Lu Hancheng, et al.2008.The analysis of nonlinear convective-symmetric instability in a rainstorm in Sichuan [J].Journal of Nanjing Institute of Meteorology (in Chinese), 31 (3): 308–316.

Ducrocq V.1993.Adiabatic and viscous simulations of symmetric instability: Structure, evolution, and energetics [J].J.Atmos.Sci., 50:23–42.

费建芳, 伍荣生, 宋金杰, 等.2009.对称不稳定理论的天气分析与预报应用研究进展 [J].南京大学学报（自然科学版），45 (3): 323–333.Fei Jianfang, Wu Rongsheng, Song Jinjie, et al.2009.Advances in synoptic analysis and application of symmetric instability theory [J].Journal of Nanjing University (Natural Sciences) (in Chinese), 45 (3):323–333.

Fischer C, Lalaurette F.1995a.Meso-β-scale circulations in realistic fronts.I: Steady basic state [J].Quart.J.Roy.Meteor.Soc., 121: 1255–1283.

Fischer C, Lalaurette F.1995b.Meso-β-scale circulations in realistic fronts.II: Frontogenetically forced basic states [J].Quart.J.Roy.Meteor.Soc.,121: 1285–1321.

Gray S L, Thorpe A J.2001.Parcel theory in three dimensions and the calculation of SCAPE [J].Mon.Wea.Rev., 129: 1656–1672.

Hoskins B J.1974.The role of potential vorticity in symmetric stability and instability [J].Quart.J.Roy.Meteor.Soc., 100: 480–482.

Jascourt S D, Lindstrom S S, Seman C J, et al.1988.An observation of banded convective development in the presence of weak symmetric stability [J].Mon.Wea.Rev., 116: 175–191.

Jurewicz M L Sr, Evans M S.2004.A comparison of two banded, heavy snowstorms with very different synoptic settings [J].Wea.Forecasting,19: 1011–1028.

寇正, 陆汉城.2005.中尺度对流系统演变中的非线性对流对称不稳定[J].大气科学, 29 (4): 636–644.Kou Zheng, Lu Hancheng.2005.The nonlinear convective-symmetric instability during the development of mesoscale convective system [J].Chinese Journal of Atmospheric Sciences (in Chinese), 29 (4): 636–644.

Lagouvardos K, Kotroni V.1995.Upper-level frontogenesis: Two case studies from the FRONTS 87 Experiment [J].Mon.Wea.Rev., 123:1197–1206.

Lagouvardos K, Lemaitre Y, Scialom G.1993.Dynamical structure of a wide cold-frontal cloudband observed during FRONTS 87 [J].Quart.J.Roy.Meteor.Soc., 119: 1291–1319.

刘还珠, 王维国, 邵明轩, 等.2007.西太平洋副热带高压影响下北京区域性暴雨的个例分析 [J].大气科学, 31 (4): 727–734.Liu Huanzhu,Wang Weiguo, Shao Mingxuan, et al.2007.A case study of the influence of the western Pacific subtropical high on the torrential rainfall in Beijing area [J].Chinese Journal of Atmospheric Sciences (in Chinese), 31 (4):727–734.

刘健文, 郭虎, 李耀东, 等.2005.天气分析预报物理量计算基础 [M].北京: 气象出版社, 121pp.Liu Jianwen, Guo Hu, Li Yaodong, et al.2005.Basis of Physics Calculation in Weather Analysis and Prediction (in Chinese) [M].Beijing: China Meteorological Press, 121pp.

刘子臣, 张健宏, 梁生俊.1997.中尺度对称不稳定的诊断应用 [J].南京气象学院学报, 20 (3): 133–137.Liu Zichen, Zhang Jianhong, Liang Shengjun.1997.Diagnosis and application of meso symmetric instability[J].Journal of Nanjing Institute of Meteorology (in Chinese), 20 (3):133–137.

陆汉城, 钟科, 张大林, 等.2002.1992年Andrew飓风眼壁区倾斜上升运动发展的可能机制——非线性对流对称不稳定 [J].大气科学, 26 (1):83–90.Lu Hancheng, Zhong Ke, Zhang Dalin, et al.2002.A possible developing mechanism of the slantwise updraft in the eyewall of the 1992 Hurricane Andrew—Nonlinear convective and symmetrical instability [J].Chinese Journal of Atmospheric Sciences (in Chinese), 26 (1): 83–90.

Maddox R A.1980.Meso-scale convective complex [J].Bull.Amer.Meteor.Soc., 61: 1374–1387.

Martin J E.1998.The structure and evolution of a continental winter cyclone.Part II: Frontal forcing of an extreme snow event [J].Mon.Wea.Rev., 126: 329–348.

蒙伟光, 王安宇, 李江南, 等.2004.华南暴雨中尺度对流系统的形成及湿位涡分析 [J].大气科学, 28 (3): 330–341.Meng Weiguang, Wang Anyu, Li Jiangnan, et al.2004.Moist potential vorticity analysis of the heavy rainfall and mesoscale convective systems in South China [J].Chinese Journal of Atmospheric Sciences (in Chinese), 28 (3): 330–341.

Novak D R, Bosart L F, Keyser D, et al.2004.An observational study of cold season-banded precipitation in northeast U.S.cyclones [J].Wea.Forecasting, 19: 993–1010.

Novak D R, Waldstreicher J S, Keyser D, et al.2006.A forecast strategy for anticipating cold season mesoscale band formation within eastern U.S.cyclones [J].Wea.Forecasting, 21: 3–23.

Persson P O G, Warner T T.1991.Model generation of spurious gravity waves due to inconsistency of the vertical and horizontal resolution [J].Mon.Wea.Rev., 119: 917–935.

Persson P O G, Warner T T.1993.Nonlinear hydrostatic conditional symmetric instability: Implications for numerical weather prediction [J].Mon.Wea.Rev., 121: 1821–1833.

Reuter G W, Yau M K.1993.Assessment of slantwise convection in ERICA cyclones [J].Mon.Wea.Rev., 121: 375–386.

Schultz D M, Schumacher P N.1999.The use and misuse of conditional symmetric instability [J].Mon.Wea.Rev., 127: 2709–2732.

Schultz D M, Knox J A.2007.Banded convection caused by frontogenesis in a conditionally, symmetrically, and inertially unstable environment [J].Mon.Wea.Rev., 135: 2095–2110.

Seltzer M A, Passarelli R E, Emanuel K A.1985.The possible role of symmetric instability in the formation of precipitation bands [J].J.Atmos.Sci., 42: 2207–2219.

Shou Shaowen, Li Yaohui.2008.Study on moist potential vorticity and symmetric instability during a heavy rain event occurred in the Jiang-Huai valleys [J].Adv.Atmos.Sci., 16 (2): 314–321.

盛春岩, 杨晓霞.2002.一次罕见的山东暴雪天气的对称不稳定分析 [J].气象, 28 (3): 33–37.Sheng Chunyan, Yang Xiaoxia.2002.Symmetry instability analysis of an unusual storm snow in Shandong Province [J].Meteorological Monthly (in Chinese), 28 (3): 33–37.

王建中, 丁一汇.1995.一次华北强降雪过程的湿对称不稳定性研究 [J].气象学报, 53 (4): 451–460.Wang Jianzhong, Ding Yihui.1995.Research of moist symmetric instability in a strong snowfall in North China [J].Acta Meteorologica Sinica (in Chinese), 53 (4): 451–460.

王亦平, 陆维松, 潘益农, 等.2008.淮河流域东北部一次异常特大暴雨的数值模拟研究Ⅱ: 不稳定条件及其增强和维持机制分析 [J].气象学报, 66 (2): 177–189.Wang Yiping, Lu Weisong, Pan Yinong, et al.2008.Numerical simulation of a torrential rain in the northeast of Huaihe basin.Part Ⅱ: Instability conditions and the mechanism of intensification and maintenance [J].Acta Meteorologica Sinica (in Chinese), 62 (2): 177–189.

Xu Q.1986.Conditional symmetric instability and mesoscale rainbands [J].Quart.J.Roy.Meteor.Soc., 112: 315–334.

Xu Q, Clark J H E.1985.The nature of symmetric instability and its similarity to convective and inertial instability [J].J.Atmos.Sci., 42:2880–2883.

徐文慧, 倪允琪, 汪小康, 等.2010.登陆台风内中尺度强对流系统演变机制的湿位涡分析 [J].气象学报, 68 (1): 88–101.Xu Wenhui, Ni Yunqi, Wang Xiaokang, et al.2010.Moist potential vorticity analysis of the evolution mechanism of a strong mesoscale convective system in a landing typhoon [J].Acta Meteorologica Sinica (in Chinese), 68 (1):88–101.

张可苏.1988.斜压气流的中尺度稳定性Ⅰ.对称不稳定 [J].气象学报,46 (3): 258–266.Zhang Kesu.1988.On mesoscale instability of a baroclinic flow.I: Symmetric instability [J].Acta Meteorologica Sinica(in Chinese), 62 (2): 243–250.