基于GPS网平差的控制基准质量检核与评定

李益斌 ，侯清华，蒋晨，陈雪元，殷爱峰，殷冠中

(1.江苏苏州地质工程勘察院，江苏苏州 215129;2.苏州阳澄湖国土资源中心所，江苏苏州 215000;3.中国矿业大学环境与测绘学院，江苏徐州 221116)

1 引言

GPS接收机所采集的数据属于WGS－84大地坐标系，不能直接作为测量成果来使用，必须对其进行坐标转换。目前常用的坐标转换方法是七参数法，七参数法进行坐标转换时，GPS网与地面网应有3个以上的重合点［1］。这些重合点是GPS网约束平差时作为基准的起算数据［2］，一般认为其无误差，但是由于等级、地域、完整性和现势性等方面的不同，这些基准点很可能带有一系列的误差，而且其坐标偏差越大，对GPS基线解算结果的影响越大［3］，对GPS网平差成果影响也就越大。有不少文献论述过GPS控制网的布设以及基准点的可靠性问题，在实践中也经常遇到基准点的误差和点位分布影响GPS约束平差精度的问题，因此需要对这些基准点进行筛选和评定，以选择合理的基准点作为平差时的约束。目前文献中的基准点质量检核常用的方法有差分法、尺度比法、基线对比法、附合导线法等等［4～10］，多是从正面论述，本文则以GPS网平差为基础，从正面和反面两个角度来进行综合论述和验证，得到了一致性的结论。

2 检核与评定控制网基准的方法

2.1 对比GPS网约束平差的结果

在进行平差解算时，不是一次性地固定所有已知点，而是逐步加以固定［11］。这里把已知控制网点划分成数个小组分别进行约束平差，其中每一组至少要有两个点。根据每组的平差结果都可以得到该组中未参与平差计算的已知控制点的坐标以及其他一些描述平差精度的特征量如PVV值、点位中误差等等。通过分析各小组已知坐标与平差坐标的差值以及特征量之间的差异，可以直观地判断出小组中各个点之间的相容情况，从而可以对这些点进行评定，选出适合参与最终平差的点。

2.2 对比已知基线边长与实测基线边长

对于高精度长距离的应用，基线解算的结果除了被用于后续的网平差外，还可用于检验和评估控制网点之间的相容情况。这是由于基线向量能够提供点与点之间的相对位置关系，而GPS对基线向量的观测精度比较高，若点位发生了变化，容易通过基线向量反映出来，从而可以采用对比基线向量边长的方法筛选和评定控制网的基准。具体的做法是:

(1)对GPS观测得到的基线向量的边长进行距离改化和投影改正，如图1所示:

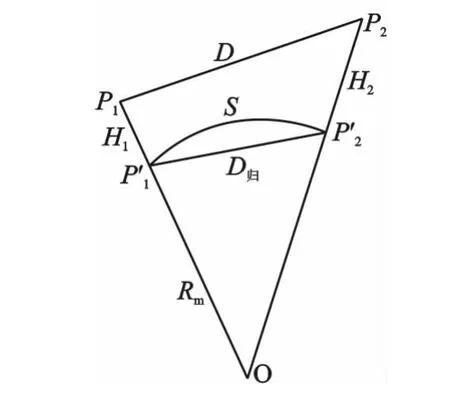
图1 距离改化及投影改正示意图

P1、P2为地面上两个已知点，其平面坐标分别为(x1，y1)和(x2，y2)，对应的大地坐标分别为:(B1，L1，H1)和(B2，L2，H2)，GPS 测得基线 P1－P2 的空间边长为D，将其归化到已知点所在的坐标系中，归化方法如下［12］:

①GPS实测空间边长归化至参考椭球面上的计算:

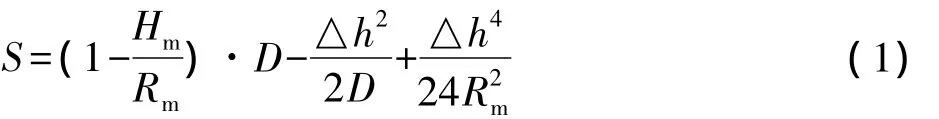
②参考椭球面上的长度归化至高斯平面上的计算:

式中:△h=H1－H2，ym=(y1+y2)/2，Hm=(H1+H2)/2，RA为测边中点的平均曲率半径(实际计算时可用地球平均曲率半径 6371 km来代替)。

(2)对比分析归算到高斯平面上的边长D归与坐标反算出的平面距离D反。

《卫星定位城市测量技术规范》CJJ.T73－2010规定，四等控制网平均边长为 2 km，最弱边相对中误差为 1/45000，故D归与D反的差异应小于 4.4 cm。

3 实例分析

选取南水北调工程某段控制网的GPS静态测量数据，该网共有10个GPS点组成，包括4个已知点GB93、LB16、6B10和GB96，网内平均边长为1392.8 m，GPS网的三维无约束平差成果的统计分析表明网的内符合精度较好。基线简图如图2所示:

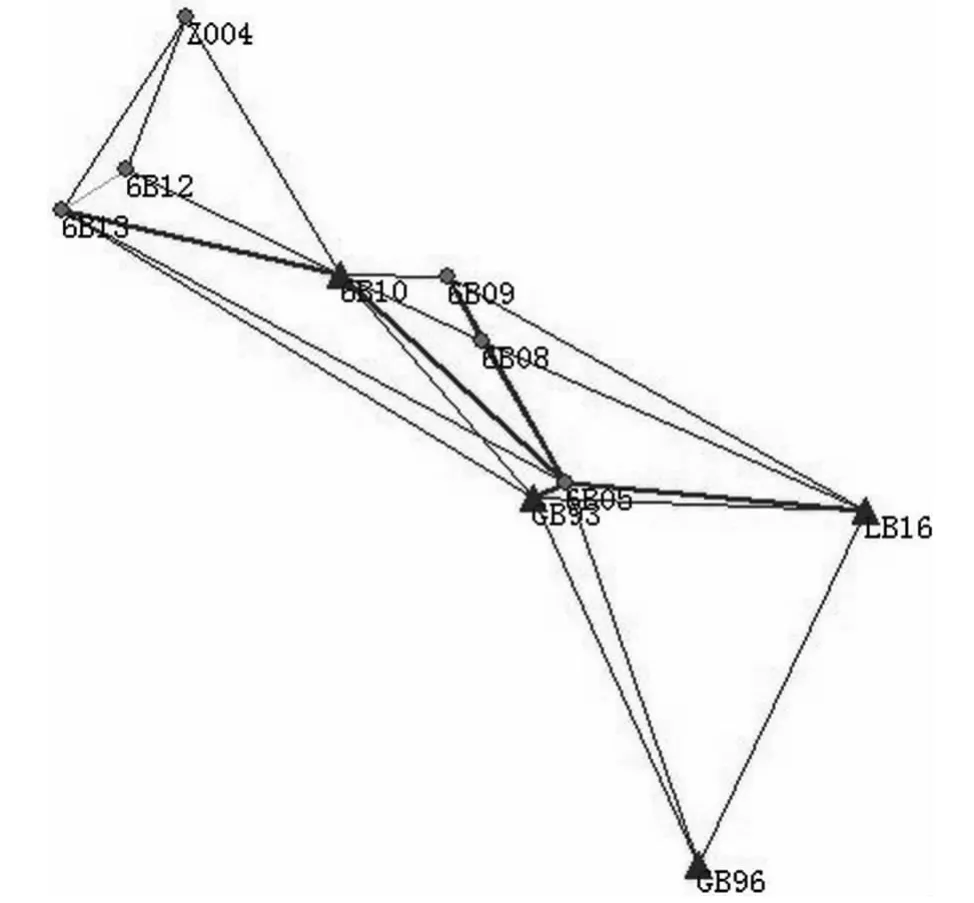
图2 GPS控制网基线简图

3.1 对比GPS网约束平差的结果

将4个已知控制点分为5种组合，分别进行约束平差，得出每组的统计量，分组及统计结果如表1所示:

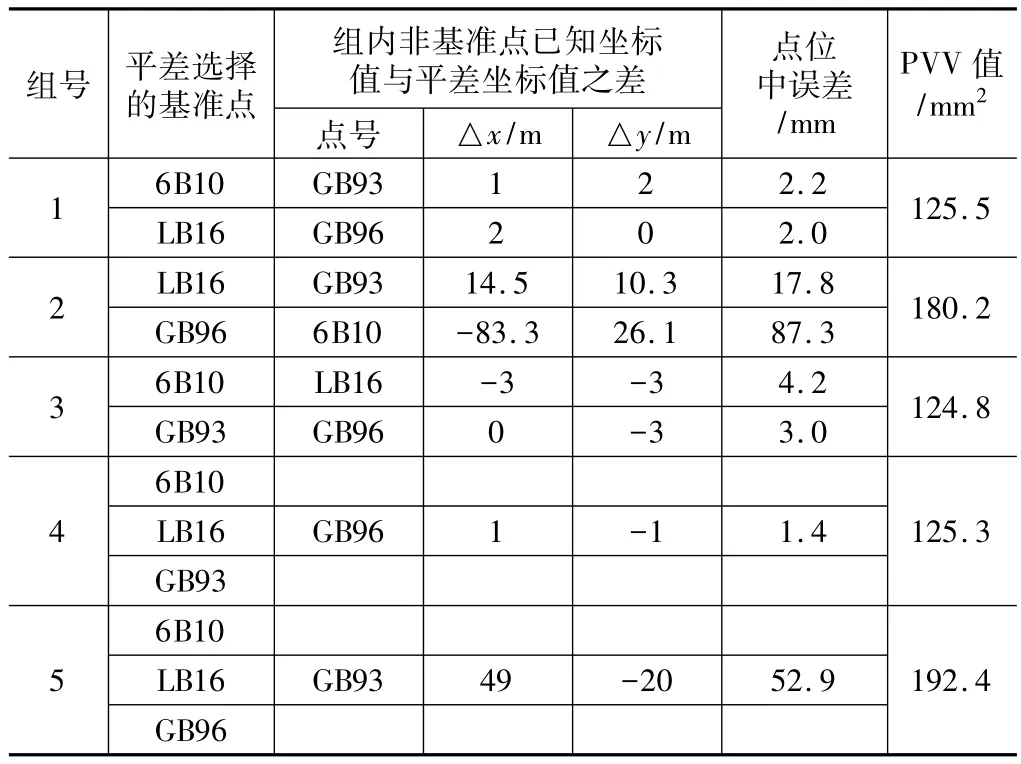
约束平差特征量统计 表1

从统计结果可以看出:第1、3、4组的已知值与平差值之差、点位中误差以及PVV值都没有明显的变化，第2组和第5组的已知值与平差值之差以及PVV值明显增大，而第2组和第5组都与点GB96的加入有关，说明点GB96含有较大误差或者与其他各点不相容，故不能作为控制基准。

3.2 对比已知基线边长与实测基线边长

采用对比基线边长的方法进一步验证。坐标反算出的基线边长及GPS实测基线边长如表2所示:

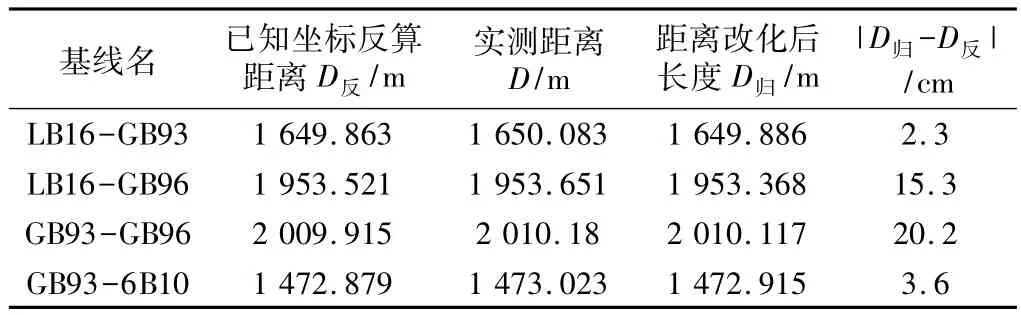
基线边长的对比 表2

由表3可知，基线LB16－GB93和 GB93－6B10的边长误差较小(分别为 2.3 cm，3.6 cm)，均小于4.4 cm;基线LB16－GB96和GB93－GB96的边长误差则较大(分别为 －15.3 cm，20.2 cm)，远大于 4.4 cm的要求。而基线LB16－GB96和 GB93－GB96都与点GB96有关，故已知点GB96可能含有粗差。

综合上述两种分析方法可知，点GB96含有粗差，跟其他各已知点不相容，不能作为GPS网约束平差时的控制基准。可以看出，这两种方法简单明了，计算简便，实用性强，效果显著，是工程实践中经常采用的方法。

3.3 误差调整后的统计分析

对未检测出粗差的控制基准进行误差调整，分析平差后的PVV值及基线边长误差的变化，以此来检核各点能否作为控制基准。这里将各组中的点6B10的误差增加 10 cm，然后对各组进行约束平差，统计其特征量如表3所示:

误差调整后的约束平差特征量统计 表3

由表3可以看出，与误差调整前相比，各组计算出的点位中误差都有了大幅度的增加，PVV值也有了较大的变化。说明对点6B10进行的 10 cm的误差调整导致该点与其他各点不相容，也反过来证明了误差调整前的该点与其他各点是相容的。同理，对点GB93和LB16进行误差调整试验也得到了相同的结论，这里不再赘述。

下面探讨误差调整后基线边长的变化。选择不含粗差的点组成的基线 LB16－GB93和 GB93－6B10，对点GB93赋予 10 cm的误差，考察基线边长的变化情况，其统计结果如表4所示:

误差调整后的基线边长对比 表4

可见，误差调整后，两条基线的D归和D反的差异都有一定程度的增大，而且都超过了 4.4 cm的限差。说明对点GB93进行的 10 cm的误差调整导致该点带有粗差，调整后不能再作为控制基准。

由此可见，误差调整后的结果从反面证明了分析平差成果及基线边长对比这两种方法的正确性。

4 结语

GPS具有定位精度高这个突出的特点，但是控制基准含有较大误差时就会影响GPS原有的高精度，最终影响网平差成果的质量，平差成果的质量可以通过控制基准的误差方便、显著地反映出来，这为合理选择GPS网的控制基准提供了一些可靠的借鉴。本文在GPS约束平差的基础上采用两种方法对已知点的检核与评定进行了理论分析，并通过实测数据进行了正面和反面的验证，两种方法一致性地剔除了粗差点，保证了GPS定位成果的精度。两种方法各有优点，但也存在着不足，如在检核误差较小的控制基准方面还不够敏感等等。因此，在实际应用中，通常是综合地采用这两种方法以及其他一些方法对已知点进行检核，以确保检核的正确性。

［1］徐绍铨，张华海，杨志强等.GPS测量原理及应用［M］.武汉:武汉大学出版社，2008，157 ～159.

［2］黄加纳.起算数据误差对平差结果的影响和检验［J］.地壳形变与地震，1998，18(3).

［3］戴中东，王瑞.起始点坐标偏差对静态GPS测量结果的影响［J］.工程勘察，2008(5):67～69.

［4］胡新玲，谭世波.GPS网中已知点间兼容性检验的探讨［J］.测绘科学，2009，34(4):103～104.

［5］邱春霞.一种检验GPS网中已知点可靠性的方法［J］.测绘通报，2004(10):30～31.

［6］冯国强，刘根友，孙秀云.GPS网参数约束平差法研究［J］.测绘科学，2007，32(5):25 ～26.

［7］吴良才，胡振琪.GPS网平面基准点的可靠性分析［J］.测绘工程，2003，12(4):39 ～41.

［8］陶波，冯林刚，刘敏.关于GPS网平面基准点的兼容性检验［J］.西部资源，2013(4):183～184.

［9］田甜.GPS网平差计算时对已知点的可靠性分析［J］.林区教学，2011(6):76～77.

［10］刘兵，王方荣.起算点对GPS控制网的影响及质量控制［J］.测绘与空间地理信息，2012(6):118～121.

［11］李征航，黄劲松.GPS测量与数据处理［M］.武汉:武汉大学出版社，2010，311 ～312.

［12］孔祥元，郭际明，刘宗泉.大地测量学基础［M］.武汉:武汉大学出版社，2010，185 ～189.