基于经验模态分解的电力系统受扰轨迹去噪方法

林 虹 陈 琳

（南京化工职业技术学院，南京 210048）

随着电网互联规模的扩大，高放大倍数快速励磁技术的广泛采用等，电网的运行更加接近稳定极限，多地出现低频振荡。因此，低频振荡模式识别方法得到了广泛地关注。

在振动测试过程中，采集到的振动信号数据由于放大器零点漂移、传感器范围外低频性能不稳定以及环境干扰往往会偏离基线，甚至偏离大小还会随时间变化（趋势项）。趋势项的存在，会使时域中的相关分析和频率中的功率谱分析产生大的误差，甚至使低频谱完全失去真实性。因此测试信号分析中常要消除趋势项，这也是信号预处理中一个重要步骤。

为提高电力系统低频振荡主导模式识别的抗噪性，提出一种基于经验模态分解的消除电力系统受扰轨迹非平稳趋势项方法，为有效辨识系统振荡模态参数提供很好的基础。

1 经验模态分解（EMD）

经验模态分解算法（EMD）可以对一个信号同时将不同尺度（频率）的波动或趋势逐级分解开来，产生一系列具有不同特征尺度的数据序列称为本征模函数（Intrinsic Mode Function，IMF），是一种全新的处理非平稳数据序列的方法，每个IMF分量具有如下特征：

1）从全局特性上看，极值点数必须和过零点数一致或者至多相差一个。

2）在某一个局部点，极大值包络和极小值包络在该点的值的算术平均和是零。

EMD分解的本质是一个“筛选”的过程，对信号x(t)进行EMD分解的步骤如下：

1）找原始信号序列x(t)的极大值点和极小值点。

2）对极值点运用插值算法进行插值并构造上下包络线emax(t)和emin(t)。

3）求上下包络曲线的均值em(t)

4）从原始信号序列中减去包络均值em(t)，得到h(t)

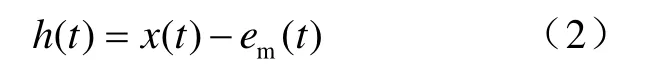
5）判断h(t)是否满足IMF的两个条件，若不满足则转到步骤 1），并将步骤 4）得到的结果h(t)作为新的输入序列，重复操作以上步骤；否则将步骤4）得到的h(t)作为一个IMF，转入步骤6）。

6）从原始信号序列x(t)中减去h(t)得到剩余项rm(t)

判断是否满足终止条件：

若满足,则算法终止，否则，进入步骤7）。

7）把剩余项rm(t)作为新的输入信号，转入步骤（1），最后得到一维信号序列的 EMD分解表达式：

2 仿真实例

2.1 四机2区域系统

以四机2区域为例，其系统结构如图1所示。

图1 四机2区域系统结构图

使用小干扰稳定分析软件 SSAT计算得到系统的区域振荡频率为 0.7Hz，局部振荡频率为 1.3Hz左右。

设置扰动：t=0s，线路8-9的首端发生瞬时三相短路，tC=0.55s故障清除，系统恢复至原状态。本例以发电机端的电压幅值，频率信号为研究对象，进行经验模态分解，去除非平稳趋势项，画出频谱图，如图2所示，其中虚线代表原始信号频谱，实线代表去除趋势项后的信号频谱。其中频谱的局部最大处对应的频率如表1所示。

图2 去除非平稳趋势项前、后信号频谱

表1 频谱局部最大处对应的频率

从图表中可以看出，去除非平稳项后，频谱的低频部分消失，但系统的区域振荡频率和局部振荡频率部分基本重合，有利于辨识系统振荡模式。

2.2 十机39节点系统

十机39节点为例，其系统结构如图3所示。

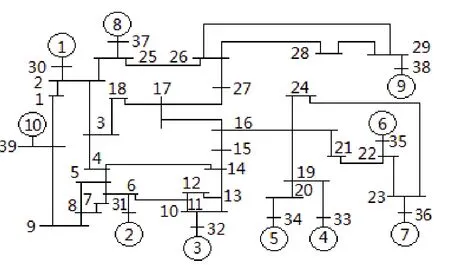
图3 十机39节点系统结构图

扰动设置不变，分析记录其39，34,30处的IMF分量模态参数，如表2、表3和表4所示。

表2 39信号IMF分量模态参数

表3 34信号IMF分量模态参数

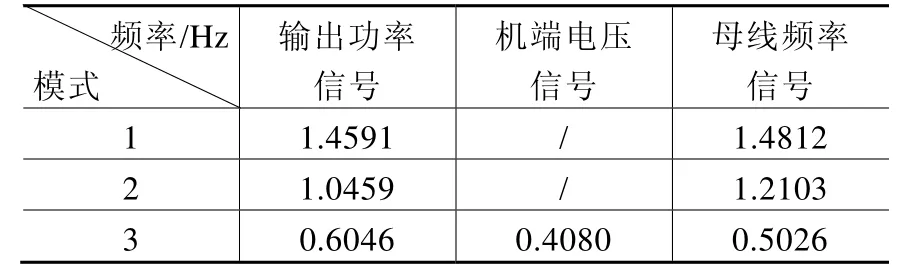
表4 30信号IMF分量模态参数

从表2至表4中数据可以验证，EMD算法能够有效提取系统主导振荡模态参数，在参与程度最小的机组的受扰轨线上提取的振荡模式信息，其误差也较大。因此，在提取系统的振荡模式时，有必要选择可观性强的轨线进行模式提取。

3 结论

本文基于经验模态，依据数据自身的时间尺度特征来进行信号分解，无须预先设定任何基函数，消除电力系统受扰信号中低频非平稳趋势项，并以4机2区域系统和10机39节点系统为例，其仿真分析说明了该方法的有效性，为有效辨识系统振荡模态参数提供很好的基础。

[1]HUANG N E.The empirical mode decomposition and Hilbert spectrum for nonlinear and non-stationary time series analysis[J].Proceedings of the Royal Society of London Series A, 1998,454(1971):903-995.

[2]经验模态分解方法及其实现[J].计算机工程与应用,2006(32):44-47.

[3]陈伟,王尚旭,啜晓宇.基于经验模态分解的属性优化方法[J].石油地球物理勘探,2013(1):121-127.

[4]王焱,朱善安.基于经验模态分解的轴承故障诊断[J].机电工程,2007,24(10):77-78,90.

[5]穆钢,史坤鹏,安军.结合经验模态分解的信号能量法及其在低频振荡研究中的作用[J].中国电机工程学报,2008,28(19):36-41.

[6]徐千茹,文一宇,张旭航,等.电力系统低频振荡综述[J].电力与能源,2014(01):38-42.