三维各向异性功能梯度材料的有限体积法

宣领宽，明平剑，龚京风，张文平，韩春旭

(1.哈尔滨工程大学动力与能源工程学院，150001哈尔滨;2.中国舰船研究设计中心，430064武汉)

功能梯度材料(FGM)一般是由两种或两种以上材料复合而成，各组分材料的体积分数在空间位置上是连续变化的，其宏观材料特性表现出梯度(逐渐变化)的性质［1］.FGM拥有高强度、耐热性、耐磨性等优势，文献［2-3］对FGM的发展进行了详细介绍.由于实际工程的需要，FGM可能是各向同性的也有可能是各向异性的.2000年以后，国内外学者围绕各向异性FGM的力学问题开展了相关研究.常用计算方法有解析法与数值法.李翔宇［4］给出了轴对称的横观各向同性FGM圆板和环板的静力学问题解析解，黄德进等［5-6］推导出各向异性FGM平面梁的弹性静力学解析解;虽然解析法能够给出精确解，并且能够灵活分析规律性的内在联系，但难以处理工程上的复杂结构问题，因此在工程实际中经常采用数值法.

目前，有限元法(FEM)是计算力学领域发展最成熟、应用最广泛的数值方法，近年来发展较为缓慢，与此同时，学者们仍然不停地发展新的数值方法.边界元法(BEM)曾在各向同性线弹性问题中获得了成功，因此有学者试图将BEM应用于各向异性、非均匀材料的线弹性问题.BEM需要求解格林函数，而材料的各向异性会使弹性矩阵中的系数增加，导致构造格林函数变得更加复杂，而且材料的非均性更会加剧这一问题.Albuquerque等［7］将BEM应用于二维各向异性材料的动力学问题，Criado等［8-9］导出指数形式的FGM线弹性体的格林函数，并基于BEM求解指数形式FGM的各向同性线弹性问题.然而到目前为止，尚未看到有学者将BEM应用于各向异性FGM的线弹性问题.此外，无网格法由于良好的适应性及避免划分网格等优势得到了广泛关注，Sladek等［10-11］将无网格伽辽金法(MLPG)应用于求解二维、三维各向异性FGM的线弹性问题，然而，MLPG法对于复杂工程问题也存在计算量大、效率低等缺点.

另一方面，在流体动力学(CFD)领域内十分流行的有限体积法(FVM)，也逐渐被应用于结构问题的求解，这么做的最终目标是采用统一方法求解多物理场(如流固耦合)问题，避免混合方法带来的一系列问题(如收敛困难)［12-13］.一般认为FEM对传统的结构自伴问题具有更高的精度，然而对于偏微分方程二者精度区别并不大［13］，而且在许多应用中二者是等价的［14］.事实上结构与流体控制方程相同，不同的只是本构方程［15］.FVM已被成功应用于结构问题，Wheel［16-17］在分析应力集中问题时，基于相同网格类型FVM获得结果的精度比FEM高，并且基于FVM解决了FEM难以解决的弹性力学中的“闭锁”现象;Fallah［18］、Demirdžic＇等［19］也将 FVM 应用于求解结构问题，但到目前，尚未看到将FVM应用于各向异性FGM线弹性问题的报道.本文采用非结构有限体积法研究正交各向异性立方体结构的静态特性，将计算结果与其他数值方法结果对比，验证本文方法的正确性;模拟横观各向同性FGM转盘结构从启动到稳定过程中的动态特性，研究密度、弹性模量沿径向变化对其力学性能的影响.

1 数学模型

1.1 控制方程

各向异性线弹性体的平衡方程［20］可表示为

各向异性线弹性体的本构方程［21］的张量形式可表示为

式中:Cijkl为弹性张量，共81个分量;εkl为应变张量．式(2)的矩阵形式为

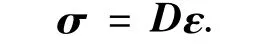
式中:D为弹性矩阵;ε为应变向量．

正交各向异性材料的弹性矩阵为

弹性轴与z轴一致的横观各向同性材料弹性矩阵D可表示为

边界条件可表示为

式中:Γd为给定位移的边界;Γt为给定牵引力的边界．T可表示为

式中n=(nx，ny，nz)为边界的单位外法线矢量．

1.2 数值离散

三维计算域采用四面体网格划分，如图1所示为任意的四面体网格单元C1234，O为C1234的重心，E12、E13、E14分别为边 12、13、14 的中点，O2、O3、O4分别为 134、124、123 的中点，空间多边形E12O4OO3、E13O2OO4、E14O3OO2为围绕节点 1 的控制体积在C1234中的边界，在围绕节点1的控制体上对式(1)进行体积分可得

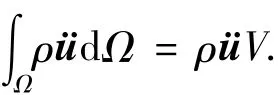
图1 三维非结构网格

应力与材料属性均定义在单元中心上，并且认为其在单元C1234内部是均匀的，对式(4)的右端第1项应用高斯定理可得

式中:四面体单元1234对节点1的贡献可以表示为σ1·A1，其中A1为空间多边形E12O4E13O2E14O3E12(由3个四边形组成)的面积矢量．因此有

对四面体单元C1234的其他节点2，3，4，同理可得

每个单元内的应力可由应变通过式(3)求得，在任意单元C1234中，应变为［22］

式中:φ为ux、uy、uz;a1=;b1=

;(x2，y2，z2)、(x3，y3，z3)、(x4，y4，z4)分别为节点2、3、4 的空间坐标;Vc为四面体C1234的体积．式(5)～(7)不仅可以用来计算Ai，而且其相当于得到应变向量ε，可以利用式(3)计算单元内的应力，因此可以将ai、bi、ci一次计算并储存起来，这样不仅使用起来方便，而且能够减少计算量、提高计算速度．

对于位移边界Γd可将边界节点的位移直接等于给定位移，对于固支边界则有=0．

若考虑静力学问题，则式(8)的左端为0.将式(8)整理为以位移为求解变量的线性方程组，可以直接求解或迭代求解，这里采用INTEL IMSL的LSARG求解器直接求解.

由于本文计算得到的应力均位于单元上，若想知道某一节点(如图1的节点1)上的应力，可由下式获得

2 数值应用

2.1 立方体结构

静态分析如图2所示，正交各向异性FGM、边长为10 m的立方体结构，来验证本文方法的正确性.边界条件为:x=0 m、y=0 m与z=0 m平面均为法向简支，z=10 m平面受到法向均布拉力σ=1 N/m2，其他各面自由.立方体为正交各向异性FGM材料，材料对应的弹性矩阵中元素为:c11=236.4×102MPa，c12=63.64 MPa，c13=18.18 MPa;c22=119.7 MPa，c23=15.15 MPa;c33=42.42×(1+z/10)MPa;c44=80 MPa;c55=c66=16 MPa.计算域采用四面体网格划分，表1给出本文采用的4种网格的相关信息.图3为AB边上的位移ux与uy，FVM、FEM结果由本文方法、ANSYS 12.0采用相同网格Grid 4得到，可以看出本文FVM结果与FEM及文献［11］中的MLPG结果吻合良好.以Grid 4的计算结果作为参考，将基于4种网格所得的边AB上的节点位移uy列于表2，可以看出随着网格数的增加，Grid3、Grid4的计算结果基本吻合;采用相同网格时，从表2可以看出FVM与FEM的计算结果几乎完全一致.

图2 边长为10 m的立方体

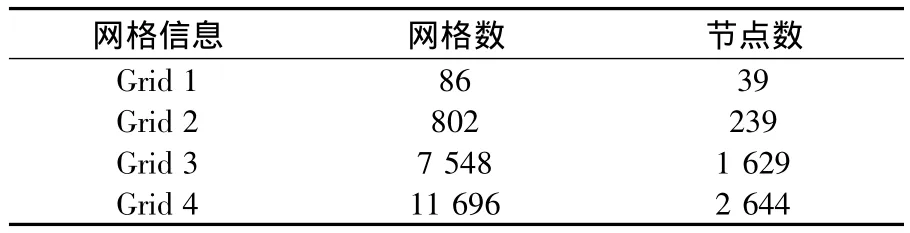
表1 计算网格信息

图3 边AB上的位移

表2 不同网格时位移uy计算结果对比(10-8m)

2.2 转盘结构

研究如图4所示围绕z轴以角速度ω旋转的转盘，几何尺寸为:内径rin=0.1 m，外径rout=0.24 m，厚度h=0.06 m，模拟转盘从启动到稳定过程中的动态特性，角速度按照式(9)规律变化.转盘内侧固支，其他自由，采用16 461个四面体网格划分，节点数为3 872，最短边长 ΔLmin=8.711 mm，时间步长可依据 CFL 条件［21］Δt≤ΔLmin/(cp)max选取．

图4 转盘结构

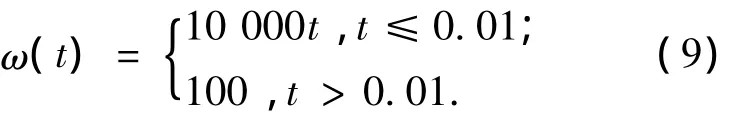
考虑以下3种均匀横观各向同性材料的转盘，其材料属性分别为

以下计算中如无特殊说明，时间步长均采用Δt=1.5 μs.3种材料的其他属性均相同，泊松比vxy=vyz=vzx=0.3，密度 ρ=8 000 kg/m3，对应的剪切模量可计算出:

由旋转产生的单位质量体力可表示为

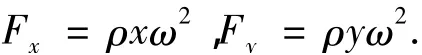
验证本文方法计算动态问题时的正确性.图5为转盘材料为M1时、t=0.015 s时，FVM计算结果与ANSYS计算结果的对比，可看出本文方法与ANSYS计算结果吻合良好，转盘的径向位移ur、轴向位移uz与径向应力σr均关于其中位面z=0.03 m对称，径向最大位移位于转盘的外径(r=0.24 m)，轴向的最大位移大概位于r=0.131 m处的上、下表面上，径向最大应力位于转盘的内径r=0.1 m.图6为中位面上各监测点径向应力σr随时间的变化，计算结果均与FEM吻合良好，随着速度的均匀增加，应力增加的越来越快，当速度保持不变后，各点的应力也保持不变.

图5 t＝0.015 s时FVM计算结果与 FEM(ANSYS)计算结果对比

图7为3种均匀横观各向同性材料不同点的时间响应，本文FVM计算结果与ANSYS计算结果吻合良好.从图7可以看出弹性模量的减少均会造成对应方向上的位移增大.

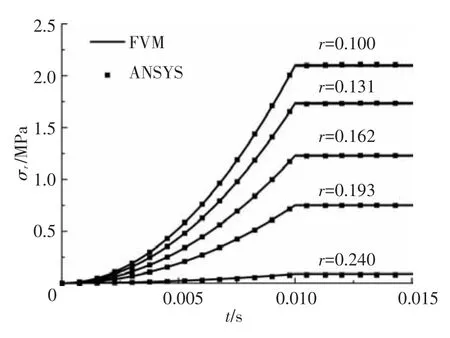
图6 中位面上各监测点径向应力σr随时间的变化

图7 3种材料不同点的时间响应

对比FVM与ANSYS计算消耗，以转盘材料M3为例，由ANSYS模态计算可得转盘的最小固有频率为1 665 Hz，则其ANSYS所采用时间步长应满足 Δt≤1/(20f)≈30 μs.表3为 FVM 与ANSYS计算消耗对比.在网格与时间步长均相同的前提下，FVM消耗较小的内存并获得较快的计算速度，其主要原因是FVM采用显格式推进求解且不需要求解大型线性方程组，而ANSYS在每一个时间内都需要建立存储刚度矩阵并求解大型线性方程组，这将会占用大量的内存及计算时间.在该算例中，虽然显格式推进求解限制 FVM采用较小的时间步长，但与ANSYS采用较大的时间步长相比，FVM仍然消耗较少的内存及计算时间.

表3 计算消耗对比

最后，考虑材料属性沿径向变化对转盘的影响，材料属性的变化规律可表示为

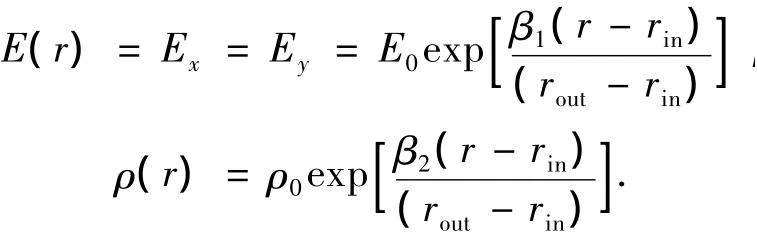
式中:β1、β2分别为梯度常数;ρ0=8 000 kg/m3;E0=100 GPa;Ez=200 GPa，其他属性保持不变.考虑4个不同梯度常数即0.0，0.1，0.3，0.5，当β1=β2=0.0对应均匀横观各向同性材料M3.如图8为中位面上r=0.24 m处的径向位移，本文FVM计算结果与ANSYS计算结果吻合良好.当β2保持不变，可以看出随着径向弹性模量或梯度常数β1的增大，转盘的径向位移减小(图8(a));当β1保持不变，随着径向密度或梯度常数β2的增大，转盘的径向位移增大(图8(b));当径向密度与弹性模量按相同趋势增大时，转盘的径向位移增大(图8(c));与弹性模量变化相比，密度沿径向变化对转盘径向位移变化有更大的影响.

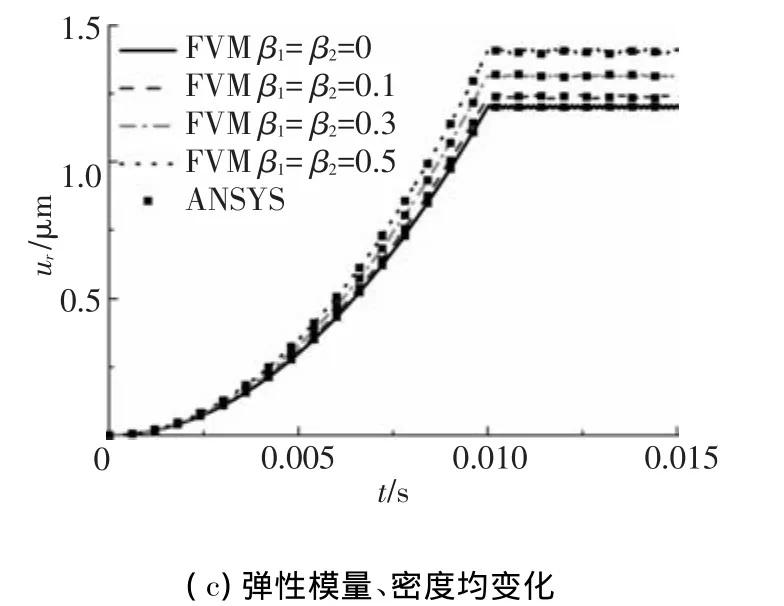
图8 中位面上r＝0.24 m处的径向位移

3 结论

1)计算结果与其他数值计算结果吻合良好，表明本文FVM的正确性.

2)与ANSYS相比，本文方法需要较小的时间步长，但占用较小内存且具有较快的计算速度.

3)研究材料属性沿径向变化对转盘的影响.结果表明:随着径向弹性模量的增大，转盘的径向位移减小;随着径向密度的增大，转盘的径向位移增大;当径向密度与弹性模量按相同趋势增大时，转盘的径向位移增大;与弹性模量相比，密度沿径向变化对转盘径向位移变化有更大的影响.

［1］王保林，韩杰才，张幸红.非均匀材料力学［M］.北京:科学出版社，2003.

［2］MARKWORTH A J，RAMESH K S，PARKS W P.Review:modeling studies applied to functionally graded materials［J］.Journal of Materials Science，1995，30(9):2183-2193.

［3］BIRMAN V，BYRD L W.Modeling and analysis of functionally graded materialsand structures ［J］.Applied Mechanics Reviews，2007，60(5):83-96.

［4］李翔宇.横观各向同性功能梯度圆板和环板的轴对称问题［D］.杭州:浙江大学，2007.

［5］黄德进，丁皓江，陈伟球.线性分布载荷作用下功能梯度各向异性悬臂梁的解析解［J］.应用数学和力学，2007，28:763-768.

［6］黄德进.各向异性功能梯度平面梁的弹性力学解［D］.杭州:浙江大学，2009.

［7］ALBUQUERQUE E L，SOLLERO P，ALIABADI M H.The boundary element method applied to time dependent problems in anisotropic materials［J］.International Journal of Solids and Structures，2002，39(5):1405-1422.

［8］CRIADO R，ORTIZ J E，MANTIC V，et al.Green’s function evaluation for three-dimensional exponentially graded elasticity［J］.International Journal for Numerical Methods in Engineering，2008，74(10):1560-1591.

［9］CRIADO R，ORTIZ J E，MANTIC V，et al.Boundary elementanalysis of three-dimensional exponentially graded isotropic elastic solids［J］.CMES:Computer Modeling in Engineering＆Sciences，2007，22(2):151-164.

［10］SLADEK J，SLADEK V，ZHANG C H.Stress analysis in anisotropic functionally graded materials by the MLPG method［J］. Engineering Analysis with Boundary Elements，2005，29(6):597-609.

［11］SLADEK J，SLADEK V，SOLEK P.Elastic analysis in 3D anisotropic functionally graded solids by the MLPG［J］.CMES:Computer Modeling in Engineering＆Sciences，2009，12(1):35-36.

［12］MANEERATANA K.Development of the finite volume method for non-linear structural applications［D］.London:The University of London，2000.

［13］SLONE A K，BAILEY C，CROSS M.Dynamic solid mechanics using finite volume methods［J］.Applied Mathematical Modelling，2003，27(2):69-87.

［14］IDELSOHN S R，OÑATE E.Finite volumes and finite elements:two‘good friends’［J］.International Journal for Numerical Methods in Engineering，1994，37(19):3323-3341.

［16］WHEEL M A.A geometrically versatile finite volume formulation for plane elastostatic stress analysis［J］.Journal of Strain Analysis for Engineering Design，1996，31(2):111-116.

［17］WHEEL M A.A mixed finite volume formulation for determining the small strain deformation of incompressible materials［J］.International Journal for Numerical Methods in Engineering，1999，44(12):1843-1861.

［18］FALLAH N.A cell vertex and cell centered finite volume method for plate bending analysis［J］.Computational Methods Applied in Mechanical Engineering，2004，193(33/35):3457-3470.

［20］程祖依.弹性动力学基础［M］.武汉:中国地质大学出版社，1989:98-106.

［21］陈明祥.弹塑性力学［M］.北京:科学出版社，2007:61-68.

［22］甘舜仙.有限元技术与程序［M］.北京:北京理工大学出版社，1988:152-154.

［23］林晓.固体应力波的数值解法［M］.北京:科学出版社，2008.