基于参考模型自适应控制的RCS研究
2014-09-21胡祝兵何生岗韩志凌冯法军
胡祝兵,何生岗,韩志凌,冯法军
(1.承德石油高等专科学校电气与电子系,河北 承德 067000;2.承德江钻石油机械有限责任公司,河北 承德 067000;3.承德石油高等专科学校社科与数理部,河北 承德 067000)
基于参考模型自适应控制的RCS研究
胡祝兵1,何生岗2,韩志凌1,冯法军3
(1.承德石油高等专科学校电气与电子系,河北 承德 067000;2.承德江钻石油机械有限责任公司,河北 承德 067000;3.承德石油高等专科学校社科与数理部,河北 承德 067000)
RCS控制策略决定了飞行器燃料消耗和姿态控制效果。以连续系统为基础,设计自适应控制律实时调整RCS控制系统的反馈参数,采用混合整数规划分配方法计算最佳的RCS开关逻辑,并对文献[5]中的飞行器模型进行仿真研究,结果表明此方法具有良好的控制效果及鲁棒性,为RLV再入时的控制策略提供理论依据。
RCS;混合整数规划;自适应控制;鲁棒性;
可重复使用运载器(RLV)在无动力巡航及再入初期,由于空气动压小,气动面操控效率很低甚至失效,且RLV主推力系统关机,此时RLV的姿态需由反作用力控制系统(reaction control system,RCS)来完成。制导系统经过指令换算,计算出姿态调整所需要的力矩,经由控制分配器计算出最佳的RCS开关逻辑,控制推力器喷管的启止,从而完成姿态控制。文献[1-3]采用PWM方式将RCS控制效果进行冲量等效来实现RCS的优化控制,此控制方式不能从理论上来保证系统的稳定性,且实现较难。文献[5]利用混合整数线性规划对RCS控制进行优化分配,减少了RCS总开关次数。文献[4]采用推力单一的RCS,虽能达到控制效果,但需要总冲大,控制精度低,且系统的鲁棒性不够好。本文以连续系统为基础,设计自适应控制律来实时调整RCS控制系统的反馈参数,采用混合整数规划RCS分配方法,仿真说明了此方法的有效性和较好的鲁棒性。
1 RCS特点
RCS控制是对推力器喷管开关的控制,通过确定喷管的点火时间,使燃料消耗和姿态控制效果达到最优[4]。推力器在开关打开时有延迟、推力上升速率、上升时间,闭合时有延迟、推力下降速率、下降时间,以及开关具有最小闭合时间限制等特性,为了研究问题的简单,本文在仿真时,将RCS开关看成具有理想的开关特性。即其输出的反作用力为:
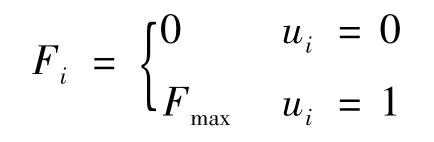
其中:Fi为第i个喷管产生的推力,Fmax为喷管的输出最大推力,ui为喷管开关指令,0为闭合,1为打开。则每一个喷管所产生的力矩为τi=ri×Fi,ri为第i个喷管离飞行器重心的距离。
2 自适应控制律设计
RLV姿态角运动方程为:
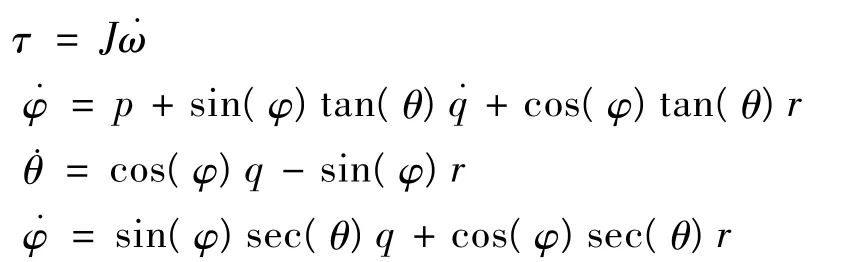
假设φ,θ均很小,可近似得:

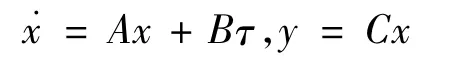
简化之后,忽略了滚转,俯仰和偏航之间的耦合。在设计控制律时可通过极点配置将系统设计成2阶振荡,且可选阻尼比ξ=0.707,无阻尼自然振荡频率ωn=3,这对简化之后的模型是可以实现,且控制能满足要求的。

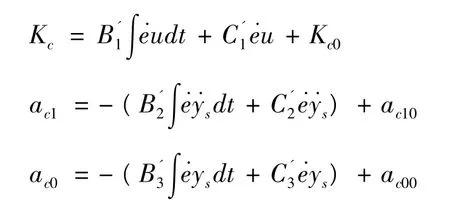
参考模型自适应控制系统的结构框图如图1所示。以俯仰轴为例,Gp(s)=为了减小系统的振荡,从而减小RCS总冲,可选择参考模型为基于lyapunov方法设计自适应控制律为:,需要通过参数寻优确定。其中 Kp=1,取 Kc0=9,ac10=6,ac00=9,采用GA 参数寻优结果为:B1=1,B2=10,B3=1.2,C1=1,C2=12,C3=15。
3 数字仿真
以俯仰轴为例,为分析问题简单,假设俯仰轴惯量为J=1,并由四个RCS单独控制偏航角,四个RCS的输出为±1 N,±9 N,RCS与重心之间的距离为1 m,并假设俯仰角初始值为0°,输入为1°的阶跃信号,分别采用参考模型自适应控制和极点配置方法,采用混合整数规划控制分配方法[5],仿真结果如图2,图3所示。
系统中存在不确定性[6],此处转动惯量加20%的不确定性,仿真结果如图5所示。

由图3—图5可知,模型跟踪自适应控制系统的跟踪精度高,RCS工作消耗的能量少,系统的鲁棒性也较好。
采用文献[5]中提供的RLV模型和RCS模型及相关参数,利用上述方法设计自适应控制器,并假设滚转角,俯仰角,偏航角初始值非别为,7.5°,15°,-15°,调整目标值均为0°,仿真结果如图6所示。可见,系统调整性能很好。
4 结论
基于Lyapunov稳定性设计的模型跟踪自适应控制器,应用于RLV再入RCS姿态控制系统中,系统跟踪性能良好,且具有一定的鲁棒性,此方法对RLV在再入初期的RCS控制系统设计有一定的参考价值。
[1]Bernelli-Zazzera F,Paolo Mantegazza P.Pulse-width equivalent to pulse-amplitude discrete control of linear system[J].Journal of Gaidance,Cotrol and Dynamics,1992,15(2):461-467.
[2]Paradiso,J.A.Adaptable Method of Managing Jets and Aerosurfaces for Aerospace Vehicle Control.Journal of Guidance,Control,and Dynamics.Vol.14,No,1,1991.44-50.
[3]Bolender,M.A.,and Doman,D.B.,”Non-Linear Control Allocation Using Piecewise Linear Functions,”Journal of Guidance,Control,and Dynamics,Vol.27,No.6,2004,pp.1017-1027
[4]贺成龙,陈欣,吴了泥.可重复使用运载器的RCS控制技术研究[J].弹箭与制导学报,2010,30(1)50-53,57.
[5]David B.Doman,Brian J.Gamble,and Anhtuan D.Ngo.Quantized Control Allocation of Reaction Control Jets and Aerodynamic Control surface[J].Gaidance,Cotrol and Dynamics,2009,32(1):13-21.
[6]Qian Wang,Robert F.Stengel Robust Nonlinear Control of a Hypersonic Aircraft[J].Journal of Guidance,Control,and Dynamics Vol 23,No.4,July-August 2000
Research of RCS Based on Model Reference Adaptive Control
HU Zhu-bing1,HE Sheng-gang2,HAN Zhi-ling1,FENG Fa-jun3
(1.Department of Electrical& Electronic Engineering,Chengde Petroleum College,Chengde 067000,Hebei,China;2.Chengde Kingdream Petroleum Machinery Co.,Ltd.Chengde 067000,Hebei,China;3.Department of Social Sciences,Mathematics and Physics,Chengde Petroleum College,Chengde 067000,Hebei,China)
The vehicle fuel consumption and attitude control effect is determined by the RCS tactics.We design adaptive control law to adjust the feedback parameters of RCS based on continuous system control theory,then calculate the optimal RCS switch logic according to mixed integer linear programming.The simulation analysis on the aircraft model in reference 5 is carried out.It shows that the aircraft control system have better performance and robustness.This method may be used in designing a controller to a RLV reentry phase.
reaction control system;mixed integer linear programming;adaptive control;robustness
V448.2
A
1008-9446(2014)03-0028-03
2013-12-11
胡祝兵(1981-),男,安徽望江人,承德石油高等专科学校电气与电子工程系讲师,硕士研究生,主要从事自动控制理论方面教学与研究工作。
