一种高精度磁性参数测试仪设计

陈 毅， 徐 勇， 张毅磊， 罗 坚

(1.湖南大学，湖南 长沙 410082； 2.中南大学，湖南 长沙 410012)

0 引 言

在特定磁化装置产生的磁化场作用下，磁性材料被磁化到饱和，当磁化场减弱为零时，样品上仍然能保留较强剩磁的材料被称为永磁材料。传统的磁性参数测试仪测试永磁材料采用模拟积分器的原理实现对感应信号的积分，同时采用硬件电路实现对积分器的调零和补偿。模拟积分器的零漂是难以克服的，硬件调零和补偿也增加了系统的复杂程度[1～3]。因此,传统磁性参数测试仪具有测试误差较大，性能不稳定、手动操作不便、系统结构复杂等缺陷。

本文以TMS320F2812处理器为核心，通过使用复化Newton-Cotes数字积分算法，不仅可以解决模拟积分器零漂的问题，而且提高了积分运算精度[4,5]。同时在DSP上使用巴特沃斯数字滤波器对采集信号进行滤波，相比于模拟滤波器有更高的精度和更好的稳定性。同时该测试仪采用软件实现系统调零和补偿，无需硬件调零电路和补偿电路，很好地解决了系统初值不为零和补偿系统在测试过程中所带来的误差。

1 数字积分理论和算法

利用A/D将磁感应线圈中由磁通量变化所感应出的模拟电动势转换为电压数字量，然后经过DSP采用合适的数字积分算法完成整个积分运算[6，7]。因此，A/D的转换精度和数字积分算法决定了测试结果的精度。本系统中采用12位采样芯片TLC2558，可以最高支持400kSPS的采样。要提高积分算法的准确度，就需要缩小积分子区间长度，即增加A/D采样的点数来实现。但是由于一般系统硬件与成本的限制，是不能任意提高采样率的，因此，可以采用高阶积分算法来提高积分精确度。然而，高阶公式由于稳定性差而不宜使用，因此，采用复化积分求积法是一个很好的办法[8]。由于永磁材料的测试是在准静态磁特性环境中进行的，因此，磁场基本上是匀速变化的[9]。假设测量线圈的初始磁通为零，运用求积公式可以求出连续变化的磁通量在某一时刻的值，积分过程可以表示如下：

tj=0+jh,j=0,1,…,n，

(1)

(2)

在子区[tj,tj+1](j=0,1,…,n-1)上使用四阶Newton-Cotes公式，将[tj,tj+1]分割为4等份，步长为h/4，分后的节点为

(3)

记为

(4)

在[tj,tj+1]上作ei(t)的四阶Newton-Cotes求积[10]

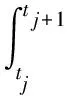
(5)

由积分区间的可加性，可得

(6)

当样品和探测线圈被置于磁化场中时，线圈中磁通量变化值从0～t的时间内为Φ

(7)

磁通量的值即是对整个[0,t]测量时间内感应电动势的变化进行积分。将[0,t]分为n等分的小区间[tj,tj+1]，设小区间的步长h=4T，T为A/D采样时间的间隔，同时,t=kh，k=1,2,…,n,则当在A/D采集的过程中时，每A/D采集4个感生电动势，k的值就增加1。

根据构造的积分公式，由此可以求出磁通变化量Φ为

(8)

同时也可以求出永磁材料在某一时刻的磁感应强度B为

(9)

2 系统硬件结构和设计

2.1 系统硬件结构

该系统硬件主要包括：霍尔探头和同心形J线圈组成的信号探测部分、DSP为核心的信号处理和控制部分、充退磁模块电路、数据传输和PC上位机部分。系统硬件框图如图1所示。

图1 系统硬件框图

硬件系统以TMS320F2812处理器为核心，工作频率能达到150 MHz，具有128 k Flash和18 k SARAM存储空间，丰富的I/O接口[11,12]。信号探测部分:霍尔探头探测由磁化装置产生的磁化电场，J线圈感应的是由相应的磁化电场产生的磁极化强度。同心形J线圈是由磁通测量线圈和磁场补偿线圈串联反接而成的[9]。DSP通过D/A转换器控制实现压控恒流源和开关电源充退磁过程。在磁化场变化的同时，感应到的信号通过信号处理模块和A/D进行数据采集。

2.2 前级信号处理电路

前级信号处理部分包括感应线圈感应产生的电压信号和霍尔探头检测的信号，其中，感应线圈感应的电压信号经过一级固定放大和二级可调放大。可调放大采用DSP控制DS1267数字电位器进行调节，前级信号的处理框图如图2和硬件处理电路图3所示。

图2 前级信号处理框图

图3 信号放大电路

2.3 A/D采集电路

TLC2558是12位低功耗、高速的CMOS A/D采样芯片，其4通道最高支持400 kSPS的采样，自带有8级FIFO，数据转换完成后，放入FIFO中等待主处理器读取数据。当与DSP连接时，可用一个帧同步信号FS来表明一个串行数据帧的开始。A/D采集电路如图4所示。

图4 A/D采集电路

2.4 D/A转换压控恒流源电路

D/A转换芯片采用TLV5618，输出模拟电压信号来控制充退磁电路，输出电压范围为0～5 V。通过线圈反向加退磁电流产生退磁场[13]。退磁电流的大小与霍尔传感器输出端产生的电动势呈正比。该芯片是12位低功耗双通道电压型输出芯片，兼容TMS320和SPI总线接口。如图5、图6所示。

图5 D/A转换硬件电路

图6 压控恒流源电路

3 系统软件设计

3.1 DSP软件设计

不同永磁材料磁性参数样品，需要设置样品的材料型号和实际尺寸。在样品测试前需要将样品磁化到饱和点进行磁锻炼，以保持试样磁状态的稳定。对于具有叠片磁轭的磁化装置，当磁化电流为零时，磁轭和极头产生的剩余磁场强度Hr并不等于零[9]。因此,需要采集零点值，并且进行软件补偿。DSP控制的D/A转换数字压控恒流源对磁化电流进行调节，同时两路A/D分别采集磁感应信号和磁化场的信号，通过IIR巴特沃斯数字滤波后，进行数字积分运算，继而将数据传送至上位机进行数据处理和显示。软件设计主流程图如图7所示。

图7 软件主流程图

3.2 上位机软件界面设计

上位机界面采用Delphi软件编写的，界面清晰简单，具有强大的数据处理功能，通过计算机与数据库相连，能够很好地显示、存储、查询、打印测试结果。

4 系统校正和测试数据

本测试系统中，采用MTC—1伏秒发生器对磁通值进行校准。伏秒发生器输出一标准的磁通，与读取到的磁通值进行比较，从而进行校准[14]。

为了将测试值和样品标准值进行对比，重复对一样品进行测试，当测试仪和磁化装置有一定发热时，观测测试数据的稳定性和重复性。其中,已测试的铝镍钴样品参数剩磁Br、矫顽力Hcb、内禀矫顽力Hcj、最大磁能积(BH)max的标准值分别为1.251 T，51.67 kA/m，52.23 kA/m，43.90 kJ/m3。铝镍钴样品具体测试记录如表1所示。

表1 铝镍钴样品10次测试数据

通过表1可以看出：样品重复测试次数为10次，通过将铝镍钴样品参数标准值和测试值进行对比，可以得出结论：剩磁、矫顽力、内禀矫顽力，磁性参数测试仪数据误差控制在0.35 %以内，同时最大磁能积的数据误差也控制在±5 %以内，测试数据误差控制明显优于传统仪器和国标的要求。

5 结束语

本文设计的高精度磁性参数测试仪充分利用了DSP核心快速数据处理的功能，复化Newton-Cotes积分算法和数字滤波提高了测试精度，软件的调零和补偿提高了系统的稳定性。本仪器适应于铝镍钴、铁氧体等永磁材料磁性参数的测量，与传统仪器相比，仪器操作简单，人机交互好，测试精度高，数据稳定性和重复性好。

参考文献:

[1] 张昌俊,彭黎辉,张宝芬.模拟积分式磁通计的研究与设计[J].新技术新仪器,2003,23(5):20-24.

[2] 黄卫萍.磁性测试系统的改进及其在永磁特性测试中的应用[D].天津:河北工业大学,2009:12-16.

[3] 匡志勇.基于USB总线的静态磁性参数测试系统的研制[D].武汉:华中科技大学,2008:5-10.

[4] 冯 坤,马 波,江志农.一种新的基于改进实时双通滤波器的信号数字积分方案[J].北京化工大学学报,2006,33(3):73-76.

[5] Nam Quoc Ngo.A new approach for the design of wideband digi-tal integrator and differentiator[J].IEEE Transactions on Circuits and Systems,2006,53(9):936-940.

[6] 刘 刚,武 丽,朱玉玉.基于CORTEX—M3微处理器的数字磁通计的研究和设计[J].数学技术与应用,2012,23(7):132-133.

[7] Zeng Long,He Yexi.Design of magnetic measurement system on SUNIST spherical tokamak[J].Plasma Science and Technology,2008,10(5):535-538.

[8] 易龙强,宋慧娜,陈金玲.复化Newton—Cotes积分算法在电能计量中的应用[J].电测与仪表,2010,47(10):15-20.

[9] GB/T 3217—92.永磁(硬磁)材料磁性试验方法[S].

[10] 刘彬清,任亚娣.Newton-Cotes数值求积公式的渐进性[J].上海大学学报,2002,8(6):503-506.

[11] 林容益.TMS320F240xDSP汇编及C语言多功能控制应用[M].北京:北京航空航天大学出版社,2009:243-262.

[12] 胡广书.现代信号处理教程[M].北京:清华大学出版社,2005.

[13] 罗 坚,王 玲.基于ARM的矫顽磁力仪的研制[J].仪表技术与传感器,2009,10(9):22-23.

[14] 王丰棋.磁通量的“伏秒”定标法[R].上海:上海第四电表厂,2005:33-54.