角点网格传导系数计算
2014-09-20梁景伟王立群郎晓彬周威皓于萌苏坤伟程超张虎臣
梁景伟,王立群,郎晓彬,周威皓,于萌,苏坤伟,程超,张虎臣
(中国石油大学(北京)理学院,北京 102249)
0 引言
油藏数值模拟即用数值方法模拟油、气、水在油藏中的运动规律,依次建立的数学模型[1]可为油藏科学合理开发、提高原油采收率等提供依据。随着计算机技术的高速发展,油藏数值模拟也发展迅速,传统规则的块中心网格已不能满足日益精细的三维地质模型描述的需要,特别是油藏数值模拟中存在断层、裂缝、尖灭等复杂地质结构以及斜井、水平井等布井方式的情况下,块中心网格存在严重的局限性[2]。角点网格的出现为克服以上问题提供了行之有效的方法[3-4]。1992年Ponting首次在油藏数值模拟中引入角点网格[5],它以8个顶点确定1个不规则网格块,对几何结构复杂的地层描述更加灵活有效[6-8],因此,被广泛应用于石油地质描述和油藏数值模拟中。
计算2个相邻网格块间的传导率是油藏数值模拟的关键步骤之一。相邻网格块间的传导率和流体性质、岩石性质、流体岩石之间相互作用、两网格块相连方向及网格几何尺寸有关。α相某一方向的传导率(Τα)可以表示为[1]
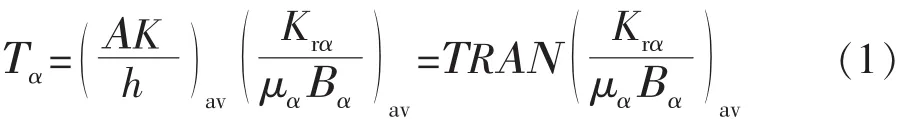
其中:α=w,ο,g(即油、水、气)。
式中:K为该方向的绝对渗透率;Α为该方向上相邻网格块的交接面积;h为相邻网格块中心在该方向上的距离;Krα为 α 相的相对渗透率;μα为 α 相的黏度;Βα为α相的体积系数;下标av表示取平均值。
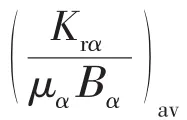
由于地层的复杂性和网格块形状的不规则性,相邻网格间的交接面形状(包括三角形、四边形、五边形、六边形)各异,也存在交接面面积为0(尖灭)或网格块体积为0等特殊情形[9-10],因此,很大程度上加大了角点网格传导系数的计算难度。油藏数值模拟软件Eclipse成功地运用了角点网格,有效地解决了复杂几何地层结构的数值模拟问题,形成了该软件的一大特色,但其技术手册中缺乏比较详细的计算思路与步骤。文献[11],[12]比较系统地推导了角点网格传导系数的计算方法,但是没有给出确定实际相邻网格间交接面形状的方法,而确定交接面形状是计算交接面面积的前提,故该方法在油藏数值模拟中难以实现。本文给出了确定复杂网格块交接面形状的方法,并将其应用到角点网格传导系数的计算中。
传导系数只与角点网格的几何结构及其内部的绝对渗透率有关,即它在油藏数值模拟过程中是1个静态变量。由于在不同模拟时间步中都要调用传导系数,其准确性直接影响数值模拟的计算结果,因此,如何准确计算角点网格中的传导系数是油藏数值模拟的关键技术之一,而准确求出相邻网格块间交接面更是角点网格中传导系数计算的核心所在。本文详细推导了角点网格传导系数的计算公式,充分考虑了油藏局部各种复杂几何结构对传导系数的影响,设计出简单有效的算法,成功地计算出相邻网格块交接面的具体形状和在3个坐标轴上的投影面积;通过编写高效的程序,针对1个有代表性的油藏实例(包括断层、尖灭等复杂情况),计算出相应角点网格的传导系数,并与通用商业软件Eclipse的结果进行对比,其结果表明本文的算法具有较高精度。
1 角点网格数据体导入与处理
考虑网格数为Nx×Ny×Nz的地层结构。在大多数商业软件中,角点网格包括2部分数据体。第1部分数据体是网格竖线两端点的坐标组成的矩阵,矩阵的列数为 6,前 3 列是竖线起点坐标(x1,y1,z1),后 3 列为竖线终点坐标(x2,y2,z2);矩阵的行数代表竖线的条数,共计
在计算与网格块(i,j,k ) 所在4条竖线的编号时,定义中间变量Lindex:
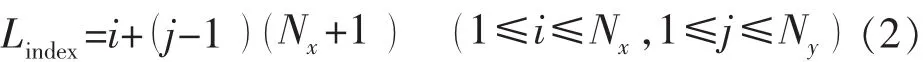
则与网格块(i,j,k) 所在4条竖线的编号(见图1)为
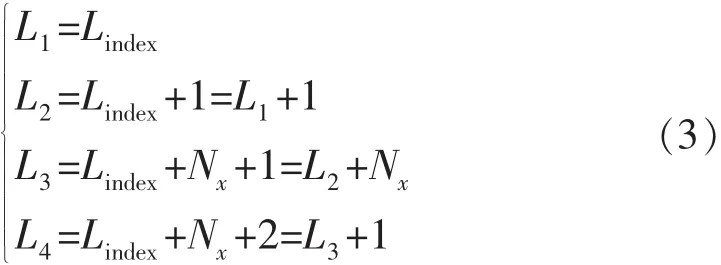
第2部分数据体表示每1个网格对应8个顶点的深度值组成的三维数据体,数据体的维数为2Nx×2Ny×2Nz。
在计算与网格块(i,j,k) 对应8个顶点的编号前,需要把以上三维数据体转成一维数据体,然后再进行计算。定义中间变量Pindex:
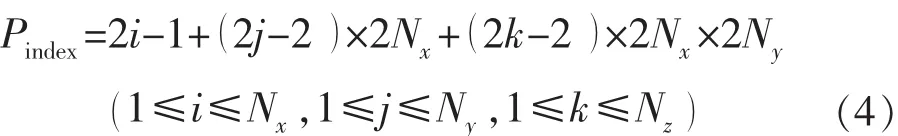
则网格块(i,j,k) 对应8个顶点的编号(见图1)为
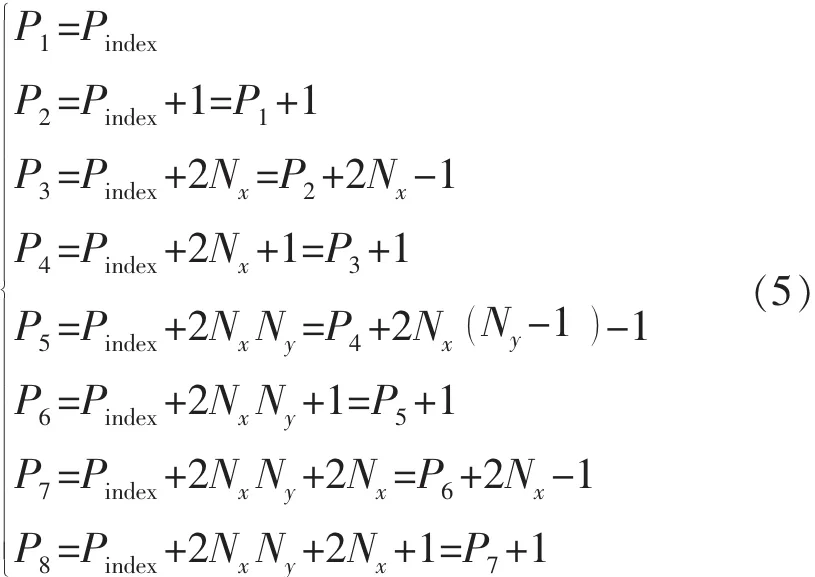
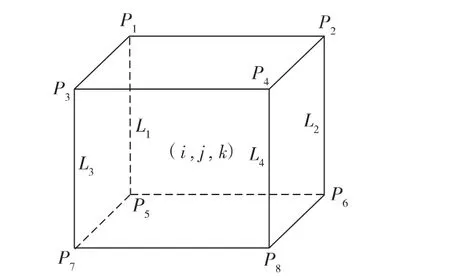
图1角点网格(i,j,k) 相邻4条线与8个顶点的编号示意
2 传导系数的计算
2.1 x方向传导系数
令I,J分别代表2个相邻网格块的一维坐标。网格块I的中心点到网格块I与网格块J相邻面(网格块I的右侧面)中心点的传导系数为
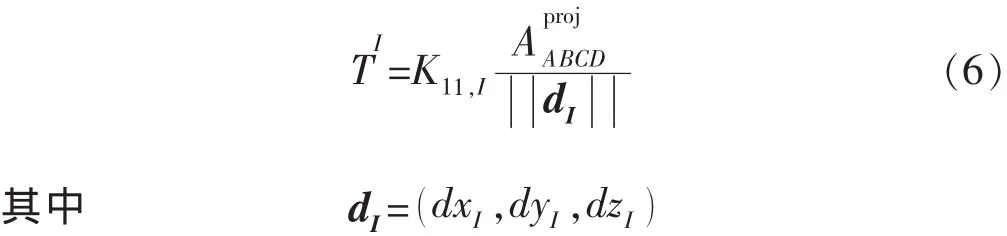
式中:K11为x方向的绝对渗透率;dI为网格块I的中心点到网格块I与网格块J相邻面 (网格块 I的右侧面)中心点的向量(见图 2)为面ABCD沿着dI方向的投影面积,m2;为向量 dI的长度,m;d 为长度,m。
如果需要考虑网格块I的净毛比RNTGI,那么该传导系数为
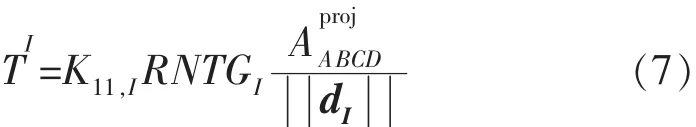
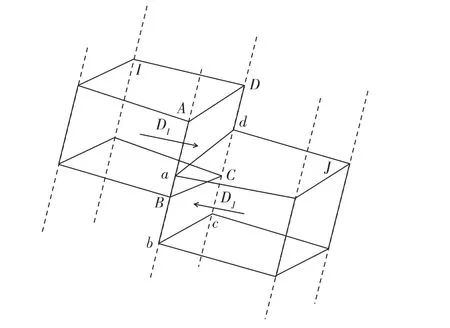
图2 角点网格示意
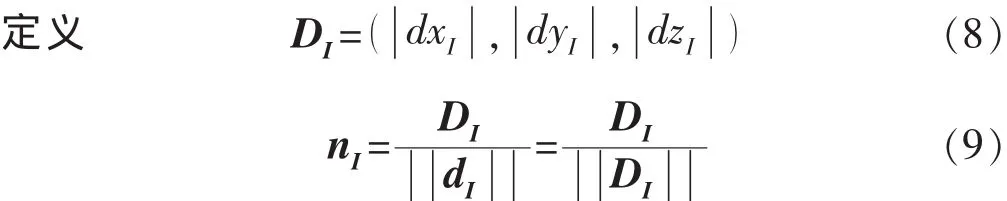

于是网格块I的中心点到网格块I与网格块J相邻面(网格块I的右侧面)中心点的传导系数为
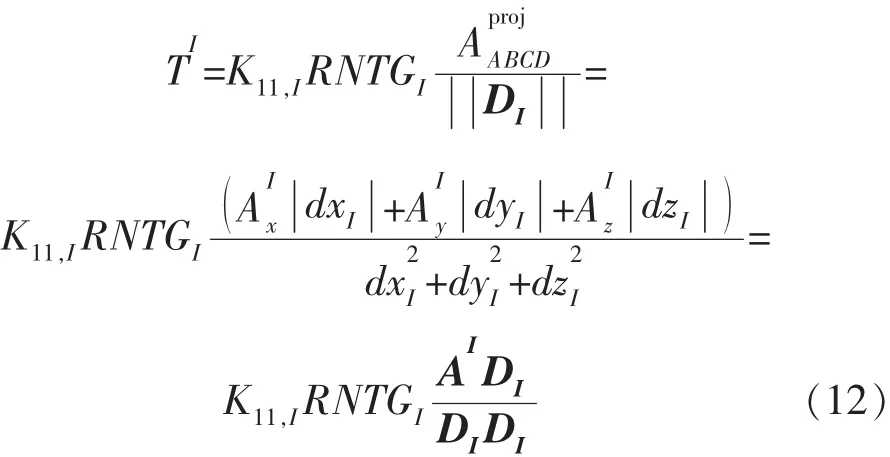
同理可得网格块J中心到网格块J与网格块J相邻面(网格块J的左侧面)中心点的传导系数TJ。TJ的计算只需将计算TI的式(12)中I标号换为J即可:
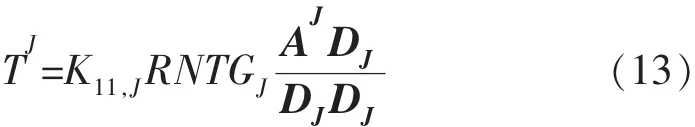
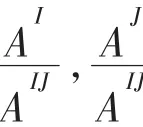
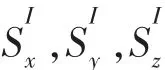
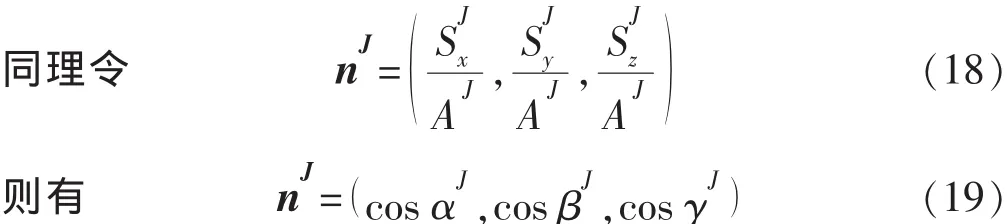
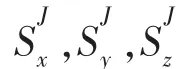
由于AI面与AJ面的单位外法线方向正好相反,即

AIJ为网格块I与网格块J交接面在x,y和z方向的投影面积的绝对值。于是式(14)可表示为
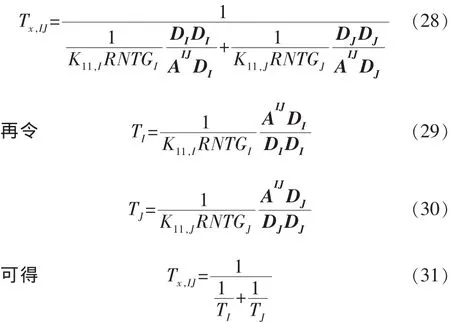
如果需要考虑单位换算,则需要引入达西常数Cdarcy;如果网格块I与网格块J之间存在断层,则需要引入传导系数乘子TMLTx,IJ,此时该传导系数为
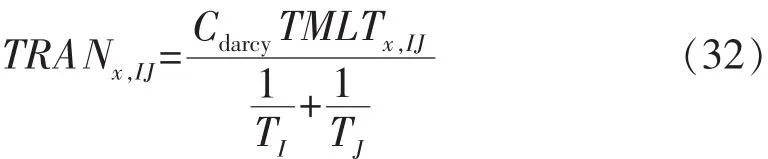
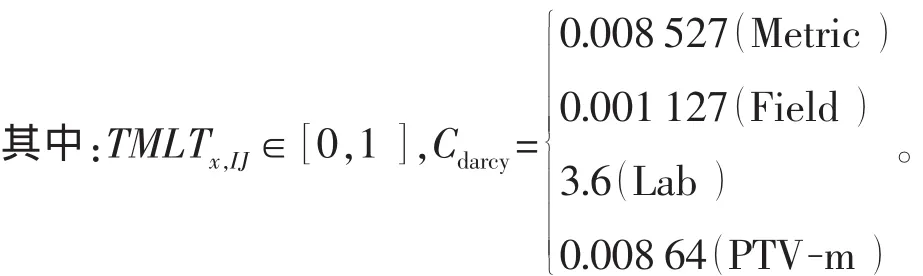
2.2 y方向传导系数
y方向传导系数的计算与x方向传导系数的计算方法相同,只需要把式(32)中的下标x改成y,并把x方向的绝对渗透率改成y方向的绝对渗透率,即
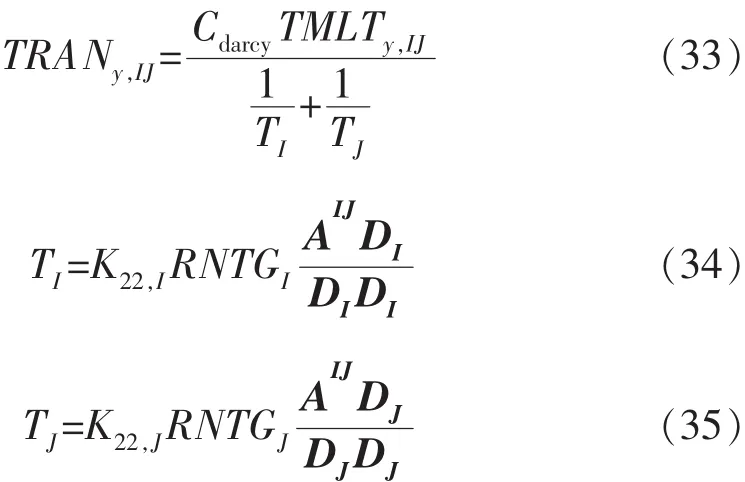
其中,AIJ,DI和DJ的计算公式分别与x方向传导系数中AIJ,DI和DJ的计算公式相同。
2.3 z方向传导系数
z方向传导系数的计算方法与x方向传导系数的计算方法相同,只需要把公式(32)中的下标x改成z,并把x方向的绝对渗透率改成z方向的绝对渗透率,但在z方向不需要考虑净毛比RNTG,即

其中,AIJ,DI和DJ的计算公式分别与x方向传导系数中AIJ,DI和DJ的计算公式相同。
由于尖灭等特殊情况的出现,某些网格块出现了体积为0的特殊情况,因此,在z方向上传导系数的计算必须对这些特殊情况加以处理:
1)若I网格块与J网格块厚度均不为0,则按上述z方向计算式(36)—(38)计算;
2)若I网格块厚度为0,J网格块厚度不为0,则z方向传导率定义为0;
3)若I网格块与J网格块厚度均为0,则z方向传导率定义为0;
4)若I网格块厚度不为0,J网格块厚度为0,则沿z方向依次向下寻找第1个厚度不为0的网格块M,然后计算I网格块与M网格块之间的传导系数,并作为I网格块与J网格块之间的传导系数。
3 相邻网格块间交接面的计算
为了计算角点网格的传导系数,由式(32)、式(33)、式(34)可知,其关键需要计算2个网格的交接面分别沿着x,y和z方向的投影面积。在图2中四边形aBCd即为2个网格块的交界面,由于4个点均位于生成角点网格的竖线上,而竖线和各点的深度值都是已知的,因此,可以通过式(3)、式(5)求得 4个点的编号及坐标。
尽管I与J之间交接面的几何结构非常复杂,但可将其分为以下3种情况处理。
3.1 相邻侧面完全重合
相邻侧面完全重合是指点A与点a,点B与点b,点C与点c,点D与点d完全重合,即网格块I与网格块J相邻的侧面完全重合。
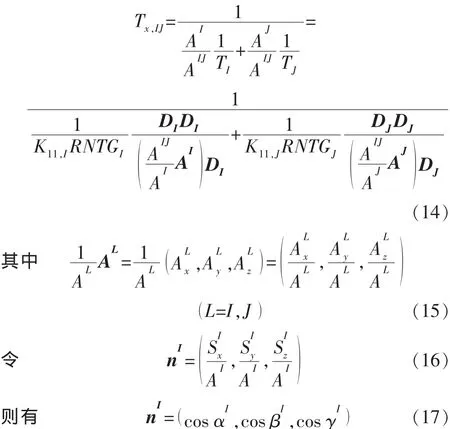
由空间解释几何理论可知,如果空间四边形ABCD(abcd)4 个顶点在同一平面上,那么,其在 x,y,z方向投影的有向面积Sx,Sy,Sz组成的向量S,可以用2个对角线向量的叉乘的一半表示,即
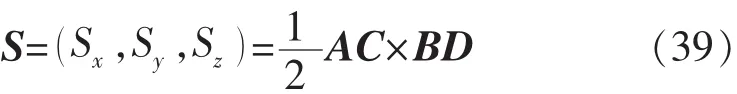
为了简单起见,即使空间四边形ABCD(abcd)4个顶点不在同一平面上,那么,其在x,y,z方向投影的有向面积组成的向量仍用式(38)进行近似处理。
由于
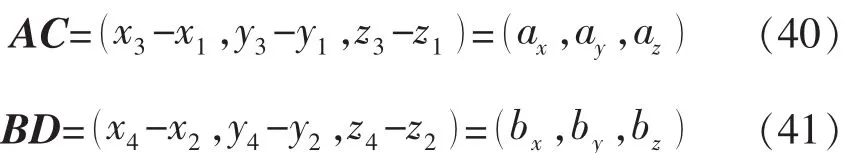
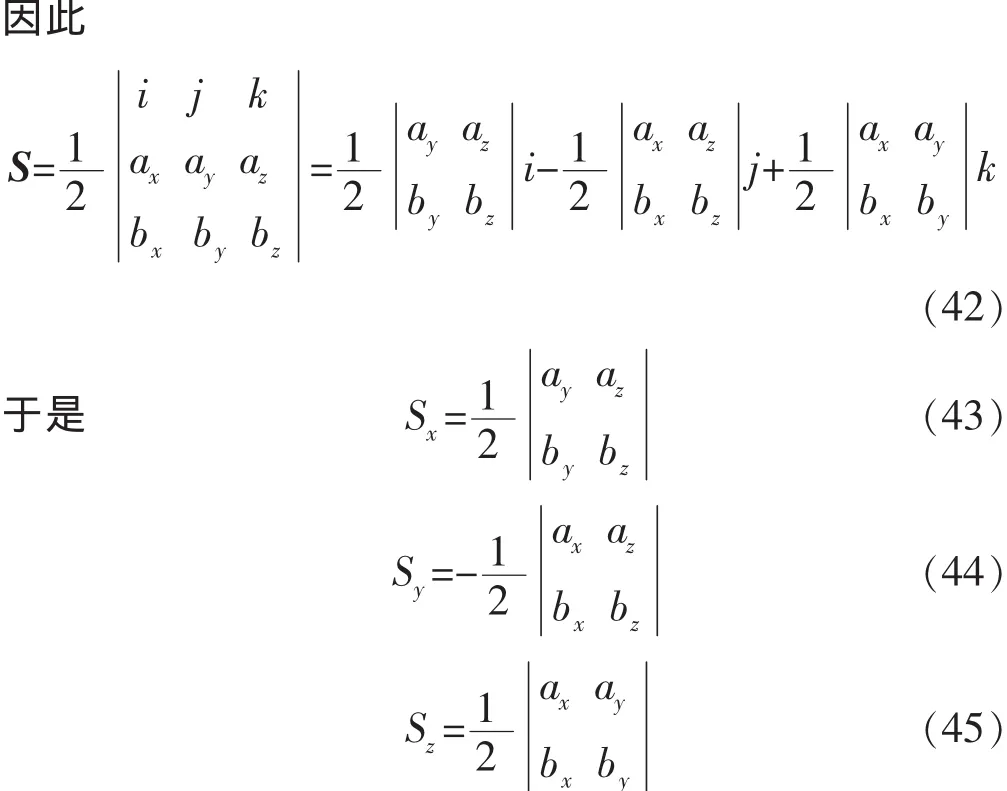
而四边形 ABCD(abcd)在 x,y,z方向的投影绝对面积分别为
3.2 无交接面
无交接面包括网格块I与网格块J相邻的侧面完全错开,或者其中1个网格块相邻的侧面面积为0,此时交接面面积为0。
3.3 交接面不完全重合
第1步:判断线段AD与ad、AD与bc、BC与ad、BC与bc是否相交;如果相交,求出相应交点坐标。
由图2可知,为了判断每对线段是否相交,把这4对线段所在的面投影到 yoz平面上,即点 A,B,C,D,a,b,c,d 在 yoz面上的投影 A′,B′,C′,D′,a′,b′,c′,d′的 x 坐标值为0。假设给定4个点坐标分别为上的投影为
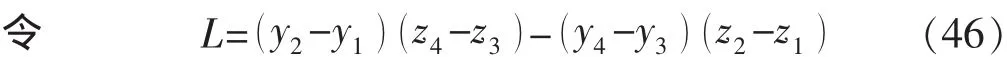
如果 L=0,则线段 A′D′与 a′d′平行或重合,即线段AD与ad无交点。否则,求交点:
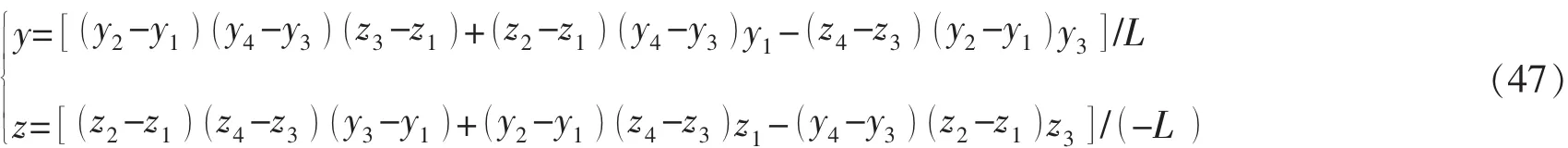
如果L≠0,且满足:
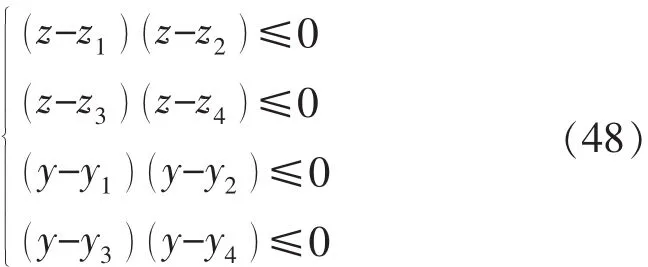
则线段 A′D′与 a′d′相交于(0,y,z)点。 否则,2 线段不相交。
由于线段 A′D′与 a′d′是线段 AD 与 ad 在 yoz面上的投影并相交,若线段AD与ad共面,则可以推出AD与ad相交,交点的x坐标为

由此得到空间线段AD与ad的交点坐标P x,y,()z。
若线段AD与ad不共面,仍用公式(49)计算出P点坐标,并将AP与PD连接成的折线近似地代替空间线段AD,同时将aP与Pd连接成的折线近似地代替空间线段ad。
第2步:判断内点。
如图2所示,判断点A,B和点a,b之间的位置关系时,若点A或点B位于点a,b之间,则把点A或点B称为内点;同理,若点a或点b位于点A,B之间,则把点a或点b称为内点。同时应注意,点A,B,a,b中最多有2个内点。用相同的方法判断点C,D和点c,d之间的位置关系,确定这4个点中的内点,如图3所示。
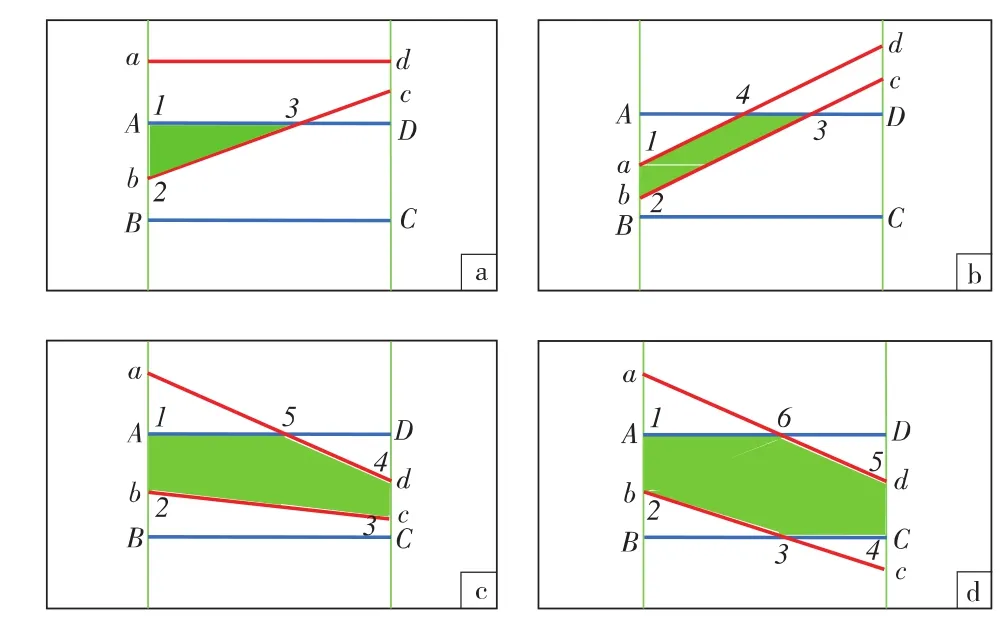
图3 相邻网格不同交接面示意
图3中,在AB边上,点A在点a和点b中间,因此,A为内点(见图3a),同理,点b在点A和点B中间,因此,点b也为内点(见图3b)。
第3步:排序。
所有内点和交点所围成的面即为网格块I与网格块J的交接面。对所有内点和线段交点,按逆时针位置关系,从A,B点所在线段开始进行排序,确定交接面顶点位置关系。如图2,交接面中只有内点没有交点,所有内点形成四边形C,d,a,B即为交接面。例如:图3d中,点 A,b,C,d为内点,点 3和点 6为交点,因此,排列顺序为 A,b,3,C,d,6。
第4步:计算交接面面积。
不完全重合的交接面可分为三角形、四边形、五边形、六边形4种,对于三角形和四边形的面积计算可按上述相邻侧面完全重合情况中介绍的方法进行计算。对于五边形和六边形,分别切为1个四边形、1个三角形以及2个四边形的组合。如:图3c为五边形,切为四边形1234和三角形451,分别计算面积;图3d为六边形,切为四边形1234和四边形4561,分别计算面积。
4 实例验证
为检验以上数值模型和程序的正确性,选择某油藏实测地层数据进行建模验证。考虑网格数为24×25×12的一个真实地层,具体地层结构见图4。
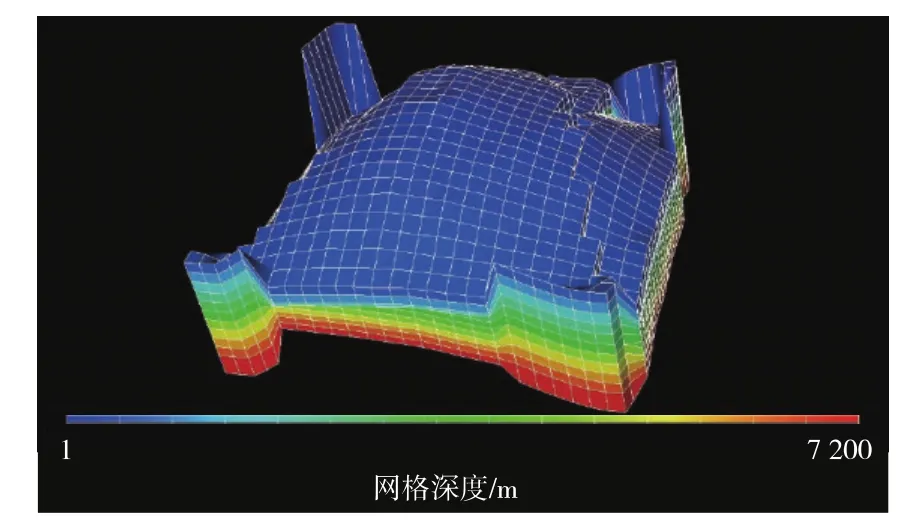
图4 地层结构示意
从图4可见,该地层几何结构复杂,包括断层、尖灭等特殊情况,比较有代表性。由于该地层结构包含了相邻网格块间交接面的各种不同几何形态,因此传导系数的计算复杂度比较高。
该地层在x,y,z 3个方向的渗透率如图5所示。

图5 某地层3个方向渗透率示意
图6显示了本文算法与Eclipse软件就该地层所计算的传导系数的绝对误差。其中,横轴表示z方向的层序,纵轴表示该层最大绝对误差值。图中数值表明,所有方向传导系数最大绝对误差为0.093,而z方向传导系数的绝对误差几乎为0。
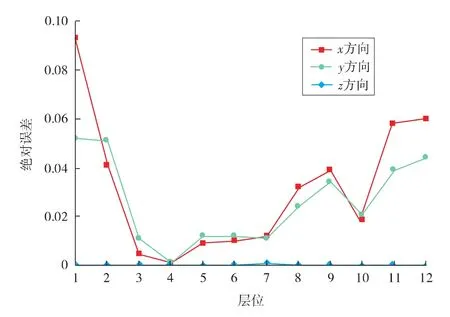
图6 本文算法与Eclipse传导系数绝对误差示意
图7显示了本文算法与Eclipse软件就该地层所计算的传导系数的相对误差。其中,横轴表示z方向的层序,纵轴表示该层最大相对误差值。图中数值表明,所有方向传导系数最大相对误差是0.010,而z方向的传导系数的相对误差几乎为0。
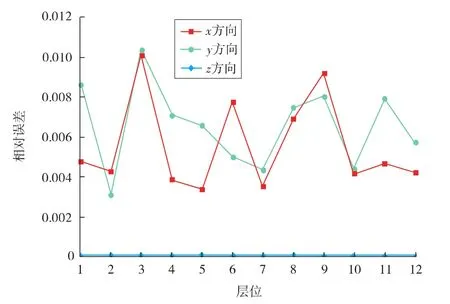
图7 本文算法与Eclipse传导系数相对误差示意
由图6、图7可见,z方向的绝对误差和相对误差几乎为0,x方向和y方向的2种误差都略大于0。产生以上结果的原因是交接面计算的精度问题。z方向上的交接面永远是四边形,而且上网格块I的下表面永远等于下网格块J的上表面,也就是说上下网格块不产生偏移;因此,z方向上的传导系数计算远比x,y方向上的传导系数简单,不同算法的数值结果差别几乎为0。由于断层、尖灭等特殊地质条件的出现,在x,y方向上,不同相邻网格块间的交接面形状差异性很大,不同的算法对该形状在各个坐标轴上投影面积的计算存在一定的差异性。但从整体上看,2种算法间的误差比较小,从工程意义上讲是可接受的。
5 结论
1)建立了基于角点网格传导系数数值计算模型。该模型充分考虑了角点网格块间各种不同交接面对传导系数计算的影响,在此基础上详细推导了传导系数的计算公式,并通过具体实例验证了算法的准确性。
2)将以上算法应用于其他实际油藏,并与Eclipse软件计算结果进行比较,其差异性均较小,说明本文算法具有广泛的适用性。
[1]Chen Z.Reservoir simulation:Mathematical techniques in oil recovery[M].Philadelphia:Siam,2007:103-129.
[2]Helnemann Z E,Brand C W,Munka M,et al.Modeling reservoir geometry with irregular grids[R].SPE 18412,1991.
[3]Ding Y,Lemonnier P.Use of corner point geometry in reservoir simulation[R].SPE 29933,1995.
[4]Ding Y.Permeability upscaling on corner-point geometry in the nearwell region[R].SPE 81431,2003.
[5]Ponting D K.Corner point geometry in reservoir simulation.The mathematics of oil recovery [M].Oxford:Oxford University Press,1992:45-65.
[6]叶继根,吴向红,朱怡翔,等.大规模角点网格计算机辅助油藏模拟历史拟合方法研究[J].石油学报,2007,28(2):83-86.
[7]毛小平,张志庭,钱真.用角点网格模型表达地质模型的剖析及在油气成藏过程模拟中的应用[J].地质学刊,2012,36(3):265-273.
[8]Juanes R,Matringe S F,Thomas L K.Implementation and application of a hybrid multipoint flux approximation for reservoir simulation on corner-point grids[R].SPE 95928,2005.
[9]Aarnes J,Krogstad S,Lie K A.Multiscale mixed/mimetic methods on corner-point grids[J].Computational Geosciences,2008,12(3):297-315.
[10]Sammon P H.Calculation of convective and dispersive flows for complex corner point grids[R].SPE 62929,2000.
[11]刘红卫,李爱华,赵国忠.角点网格传导率计算技术研究[J].大庆石油地质与开发,2005,24(6):35-36.
[12]计秉玉,赵国忠,李洁.多学科集成化油藏研究方法与应用[M].石油工业出版社,2009:85-96.
