基于元胞自动机的交通事故影响下车辆的跟驰行为分析

陈淑燕，于泳波，舒航，陈茜

(东南大学 交通学院，江苏 南京 210096)*

0 引言

本文研究城市道路交通事故影响传播，探索城市道路路段交通事故影响下的交通流特性，确定交通事故影响范围，为交通事故的处理提供理论依据.国外对交通事故影响传播机理的研究主要集中在道路交通事故影响分析方面，德国和瑞士通过调查研究得出一起行车事故平均可能找到1.5～1.6个影响因子的结论.Frank Schoroeder等人对典型路段进行了仿真分析［1］，对于经济车速的提出以及相关研究提供了一种思路.国内部分研究者对事故影响、车流波传播等进行了研究，如吴正和王建军分别建立了模拟高速公路交通事故干涉车流波的非线性［2］和线性［3］交通流数学模型，能够模拟交通事故引起的车流波传播过程.

基于此，本文通过对城市道路交通事故影响下的交通参数以及车流波模型进行研究分析，改进元胞自动机模型构建交通事故影响量化模型，估计交通事故影响面积、排队长度、持续时间等，从而确定交通事故对城市道路路段的影响范围，为交通控制及事故处理提供理论依据.

1 元胞自动机原理

元胞自动机［4］(cellular automata 或 cellular automaton，简称CA)实质上是定义在一个由具有离散、有限状态的元胞组成的元胞空间上，按照一定的局部规则，在离散的时间维度上演化的动力学系统.

元胞传输模型(the Cell Transmission Model)［5］是Daganzo提出的一种和流体动力学模型相一致的离散形式的模型，可用于描述交通流的干扰和交通事故影响下的交通流.对于多车道交通流问题，Rickert对双车道交通流进行了深入研究［6］，主要提出了车道变换规则.Biham，Middleton和Levine提出了BML模型［7］，该模型定义于一个N×N方格网上，是基于184号规则的二维交通流元胞自动机模型.

传统的交通流元胞自动机模型大多以路段为元胞.在考虑车辆速度时，NS规则和184号规则［8］均将前车视为静止从而研究跟驰车辆的速度，由此造成模拟速度小于实际车辆速度，对伴有随机慢化的交通流，所得流量远小于实测数据.

基于此，本文提出一种改进的元胞自动机模型，应用于交通事故影响下交通流的跟驰特性分析.该模型以车辆为元胞，以车辆跟驰模型和车道变换模型确定元胞状态.

2 元胞自动机模型构建

2.1 交通事故的影响与模型要素的类比分析

交通事故的影响与元胞自动机模型要素的类比关系见附表.

附表 交通事故的影响与模型要素的类比

2.2 元胞模型及演化规则

2.2.1 模型的基本假设

①事故的发生仅堵住了一条车道，相邻的同向车道不受影响;②没有发生事故的车道车辆运行严格遵循跟驰模型，不考虑随机慢化因素的影响，并且不会选择变道;③当发生事故的车道形成排队时，仅允许排队车辆的第一辆车择机变道;④同一车道，后车状态仅与前车状态相关;⑤假设在短时间内事故影响程度不变.

元胞由泊松分布随机产生，车辆从len长的车道起点行驶.在不受事故影响时，车辆保持稳定的速度vm行驶，且不会变换车道.在发生事故的车道上，当车队的第一辆车发现前方事故时，会选择变道行驶.当通过事故影响范围后，即刻选择变回原来的车道.当速度达到稳定时，元胞消亡.

2.2.2 改进车辆跟驰模型

受事故影响的车道，后面的元胞速度仅由相邻前面的元胞决定，遵循非线性车辆跟驰模型［5］.由于本文以车辆个体作为元胞进行研究，因此，对上述模型稍加改动，得

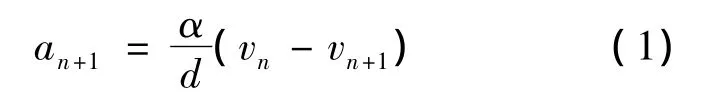
式中，an+1为第n+1辆车的加速度;d为相邻两辆车的距离;vn为第n辆车的速度;vn+1为第n+1辆车的速度;α为比例常数.

2.2.3 简化绕行变道模型

当第一辆车到达事故现场时，为了通过该路段，会择机变换车道绕行，遵循车道变换模型.与Rickert双车道交通流变道规则 不同的是，本文依据跟驰模型确定车辆的速度，速度的变化是连续的，且加入了事故影响程度系数，更符合交通事故影响下的交通流特点.由于本文所有变道过程均由于遇到障碍物之后强制变道，所以笔者将车辆遇到障碍物的绕行和车辆的变道结合起来，建立了特殊的绕行变道模型.具体规则如下:

记lo为事故发生车道最靠近事故现场的车距离事故发生点的距离，该车将会在面对障碍物后进行减速并择机变道.无论之前的车速多少，在直接面对障碍物时，车辆均会减速至一个较低水平绕过障碍物.因此，假设所有车辆均以一个当量速度直接“穿”过障碍物，这个当量速度一定小于常规车速，而且和车辆之前的速度无关，仅与事故影响程度有关.记事故影响程度系数为β(0＜β＜1)，影响程度越大β越小.此β值得确定需要根据以往数据处理而得，下文实际验算中β取0.4.

如图1，dk+1为n车车头距离相邻车道上前方车辆第k+1车的车尾的最小值，dk为该车车尾距离相邻车道后方车辆第k车的车头的最小值，dmin是车辆车道变换所需要的最小长度(这里取5 m)［10］.k和k+1车的初始速度均为v1，v1＞v0.

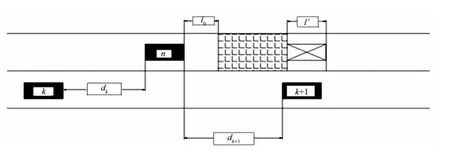
图1 车辆变道绕行示意图

n车变换车道需要满足与k车和k+1车的安全距离.本文从以下几个方面考虑:

(1)k+1车的限制

由于k+1车在n车的前方，因此n车变道不影响k+1车的状态，此时只需要考虑两车的安全距离.即当dk+1≥dmin时，认为k+1车对n车的变道不产生影响.

(2)k车和n车的相互影响

两车的相互影响主要体现在必须时刻保证安全距离.当n车开始进入车道2时，k车需要一个加速度a以保持其与n车的距离，且a应该是t时刻的dk以及vk的函数.

可得车辆可以变道行驶的条件为

3 仿真分析

根据构建的数据结构，可以用MATLAB语言编写仿真程序.在仿真系统［11］中，仿真参数如下:

事故影响等级取β=0.4，事故发生位置在400 m处，事故遮挡车道数为1，事故遮挡长度为50 m.

图2记录了所有小车在某一时刻的位置，每个小车在某一位置都会以点的形式记录在图上，纵坐标显示了该位置时的记录时间.最左边为未受影响的匀速度运行，由于采用了泊松分布模型，所以线条粗细相见，较符合实测图像.可以看出，最下面的若干条曲线几乎未受太大的影响，保持一个较为稳定的斜率(实际上就是小车的速度).而当小车渐渐增多时，就会发生明显的被动超车现象(受阻车道上的车辆减速，被另一车道上的车超过)，而且整体的车速会降低.此外，还可以从这张图中看出明显的周期性车速损失，反映在图中就是在400～600区域明显的间隔交叉条纹.

图2 车辆位置－时间分布图

图3则直观地表现了交通事件对不同路段的影响.虽然障碍物位于400 m处，但是由于跟驰模型以及车速传播，车流在300 m之前就有相当影响.大部分车辆将会在0.4 m/(0.1 s)之后以曲线恢复到正常车速.

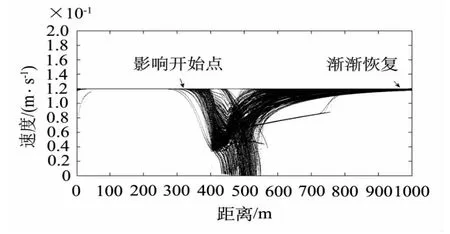
图3 车辆速度－位置散点图

4 结论

本文通过构造一个更接近实际交通流分析的连续状态集元胞自动机模型，模拟出在给定车流参数下，双车道上发生交通事故之后的状态传播和消散的结果。通过对数据结果的图形化分析，发现障碍物对整体交通流的影响要远远超过实际上的物理范围，而且此影响的消散也非线性，整个速度的损失波及到很远(上述模型影响到了障碍物600 m以后).此外，障碍物处物理阻挡造成的速度损失还会向前传播，影响到障碍物之前的车流.

［1］FRANK SCHROEDER，BERT BREUER，HELMUT PREISS.Motorcycle Noise and Exhaust Emissions-Statutory Testing Methods Versus Real Traffic Situations［J］.SAE，1999(1):3255.

［2］吴正，汪茂林.高速公路交通事故和干涉车流波的非线性数学模型［J］.西安公路交通大学学报，2001，21(2):80-83.

［3］王建军.交通事件和干预作用影响下的高速公路车流波分析［J］.重庆交通学院学报，2006，25(6):106-110.

［4］贾斌，高自友，李克平，等.基于元胞自动机的交通系统建模与模拟［M］.北京:科学出版社，2007:9-16.

［5］DAGANZO CARLOR F.The cell transmission model:A dynamic representation of highway traffic consistent with the hydrodynamic theory［J］.Transportation Research Part B，1994，28B(4):269-287.

［6］RICKERT M，NAGEL K，SEHRECKENBERG M，et al.Two lane traffic simulations using cellular automata［J］.Physica A，1996，231(4):534-550.

［7］BIHAM O，MIDDLETON A，LEVINE D.Self-organization＆ a dynamic transition in traffic flow models［J］.Phys.Rev.A，1992，46:6124-6127.

［8］WOLFRAM S.Theory and applications of cellular automata［M］.Singapore:World Scientific，1986.

［9］HUI FU，JIANMIN XU，LUNHUI XU.Traffic chaos and its prediction based on a nonlinear car-following model［J］.Journal of Control Theory and Applications，2005(3):302-307.

［10］WEI LV，WEIGUO SONG，XIAODONG LIU，JIAN MA.A microscopic lane changing process model for multilane traffic［J］.Physica A:Statistical Mechanics and its Applications，2013(1):1142-1152.

［11］谭惠丽，刘慕仁，孔令江.单速及多速车道元胞自动机交通流模型研究［J］.广西师范大学学报，2002，20(2):8-11.