改进GPC算法在永磁同步电机控制系统中的应用
2014-09-20赵肖旭黄声华王正昊周竞孙耀程华中科技大学电气工程与电子工程学院湖北武汉007国网新乡供电公司河南新乡500河海大学能源与电气学院江苏南京00南京航空航天大学自动化学院江苏南京006
赵肖旭,黄声华,王正昊,周竞,孙耀程(.华中科技大学 电气工程与电子工程学院,湖北 武汉 007;.国网新乡供电公司,河南 新乡 500;.河海大学 能源与电气学院,江苏 南京 00;.南京航空航天大学 自动化学院,江苏 南京 006)
0 引言
永磁同步电动机(PMSM)具有高功率密度、高效率、高可靠性等优良的动态特性,而且过载能力强、转矩密度大,逐渐成为新型电梯拖动系统发展的主流。由于PMSM转子磁场的方向与转子位置一致,所以按转子磁链定向矢量控制实现比异步电机简单,适合矢量控制变频器。
从控制观点看,PMSM调速系统往往是需要快速响应且动态性能高的系统。通常的解决方案是采用PI控制器串联于控制回路。通过串联PI控制器可以方便地配置系统的工作点,从而提供了更大的调整范围。然而,为了使系统获得更好的动态性能,需要设置合适的PI参数以满足永磁同步电机的控制需求。对于PI参数的设置则经常需要依靠经验来不断尝试获得,这给实际运用带来了一定的麻烦。
本文讨论的方案是基于更详细的数学分析的永磁同步电机控制系统设计。基于模型的算法可以优化控制过程,可以自然地生成与实时操作要点相关的控制行为。如图1所示为预测控制基本结构。D.W.Clarke等提出的GPC算法就是一种很有发展前景的基于模型的控制算法,它通过在控制过程中产生预测输出序列,以使系统性能指标达到最优。但也有其固有缺陷,如计算量较大、算法过于复杂等。所以,本文采用金元郁等提出的基于CARIMA模型的JGPC对PMSM的控制进行研究。这种算法简单、计算量较小,保留了GPC的基本特征和优点。在系统中,速度环CARIMA模型中含有机械阻尼系数、转动惯量等机械参数,这些参数在电机运行的不同时期会产生一定的变化,定时的运行在线辨识程序能够实现对模型参数定时更新,抵消因参数变换引起的模型误差。
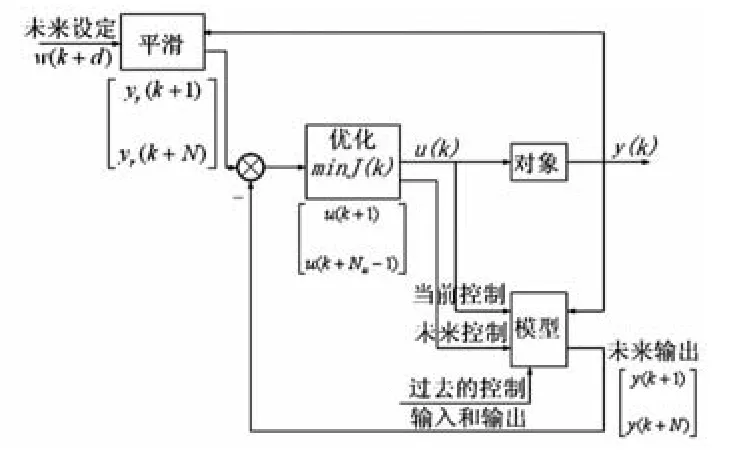
图1 预测控制的结构
1 永磁同步电机驱动系统的CARIMA模型
文献[1]介绍了广义预测控制及其他系统辨识与自适应控制算法,根据介绍的方法,设计一种PMSM的速度环CARIMA模型。
假设磁路不饱和,忽略磁滞、涡流损耗,PMSM在d-q旋转坐标系中的模型表达式为:

式(1)中ψr为转子磁钢在定子上的耦合磁链,Ld、Lq分别为永磁同步电动机的直、交轴主电感,id、iq分别为定子电流矢量的直(d)轴、交(q)轴分量,ψd、ψq分别为 d 轴、q轴磁链,ω 为转子电角速度,Rs为定子电阻,p为极对数。
传动系统机械运动方程为:

式(2)中 T为电机电磁转矩;TL为负载转矩;J为转动惯量;B为阻尼系数(包括风阻与粘滞系数),(r为机械角速度,ωr=ω/p。
取以转子磁场定位的矢量控制方式,令id=0,则电机的电磁转矩T只和iq有关,T将正比于q轴电流iq,即:

式(3)中 kT=3/2pψr,再令 TL=0,由式(2)得 PMSM 机械运动开环传递函数:
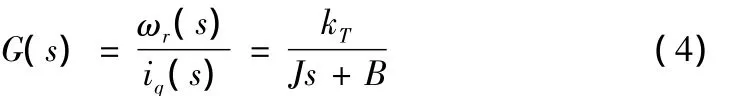
对式(4)加入零阶保持器,并进行z变换后得PMSM机械运动z传递函数:

式(5)中 a= - e-T,B/J,b=kT(1 - e-T,B/J)/B,Ts为采样周期。
这里将负载转矩TL看做系统扰动折算后写入方程,可得如下系统差分方程:

式(6)两边乘以差分算子iz-1,写成如下形式:
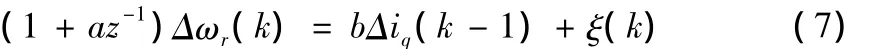
其中ζ(k)=cΔTL(k)为负载转矩波动的函数,可以看做系统的噪声。
则系统CARIMA模型为:

式(8)中 A(z-1)=(1+az-1)Δ =1+(- 1+a)z-1- az-2,B(z-1)=b。
2 广义预测控制器的设计
2.1 基于CARIMA模型的改进GPC控制律
由式(8)递推,系统将来时刻的最小方差输出模型[2-3]为:

式(9)中,

式(10)中的ωm(k+j)完全由过去的控制输入和输出确定,可由下式推出:
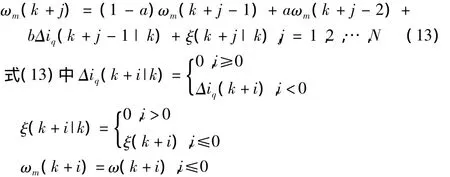

若令ω*为参考转速,则目标函数为:

将(9)式带入(15)后,对Δiq求偏导,得GPC控制率:
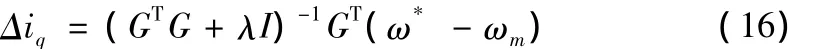
则当前时刻的控制量为:

式(17)中λ为控制量加权项。
式(12)中矩阵元素由右式递推算出:
2.2 CARIMA模型参数在线辨识
PMSM在运行过程中,模型参数会随之产生一定的变化,这种变化将会导致2.1节中所提及的CARIMA模型不准确,进而影响预测控制器的性能。由于在电机实际运行过程中,电机参数的变化是非常缓慢的,故只需对参数进行定时的在线辨识和更新就可以解决模型不准确的问题。在线辨识模型参数的方法有很多种,最常见的就是递推最小二乘法(RLS)。RLS是一种适用于定常系统参数未知的参数在线辨识算法,但多数实际系统模型参数是时变的,在参数随时间缓慢变化的同时,算法本身对参数的修正能力也越来越弱,使新采集的输入输出数据对参数估计值的更新作用不大。为了克服这个问题,本文使用了带遗忘因子递推最小二乘法。
应用于本系统的参数辨识方法[4]如下:

式(18)中θ为待估参数矩阵,φ(k)为k时刻之前的输入和输出矩阵。^

3 传统GPC算法与改进GPC算法在永磁同步电机控制系统中的应用对比
GPC算法所用CARIMA模型与改进GPC算法模型一致。建立CARIMA模型后,需要引入Diophantine方程[5]:
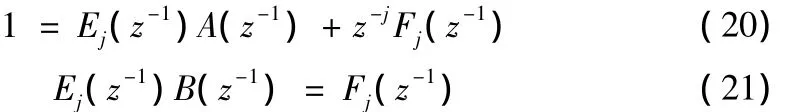
GPC所用的预测输出模型矩阵形式为:

上式的系数矩阵是根据Diophantine方程的结果求出的。矩阵方程组的计算过程较复杂,计算时间较长,占用系统资源较多,不利于基于DSP的实际应用。本文采用的改进GPC用新的途径建立预测模型,避免了求解矩阵方程组等复杂运算,而且这种算法不像传统GPC那样受到了C(z-1)稳定的限制。其算法简单、计算量较小,基本保留了GPC的基本特征和优点。
4 系统仿真及分析
采用MATLAB软件对改进广义预测控制器仿真实验。永磁同步电机参数如表1所示。
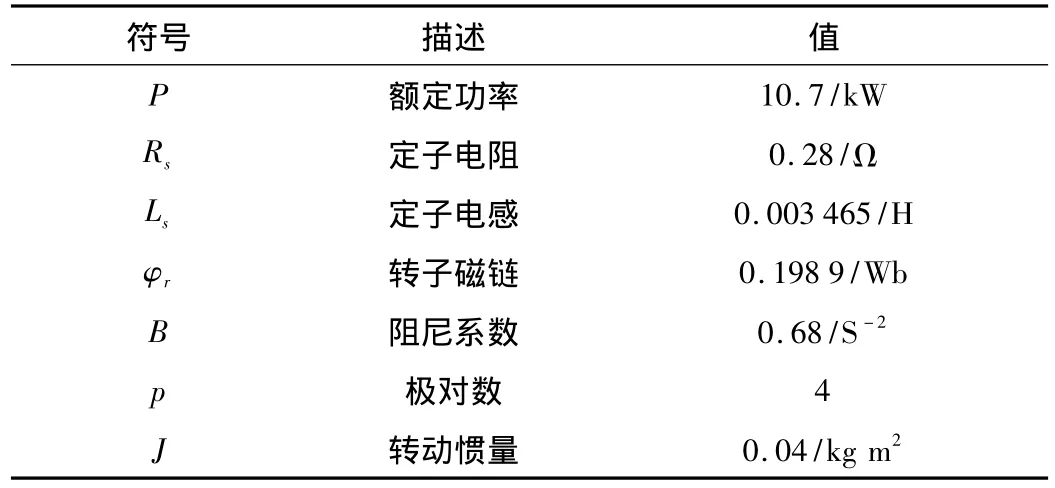
表1 永磁同步电机参数表
文中改进广义预测控制器的采样周期取0.001 s,预测长度取8,输出柔化系数为0.7,辨识算法遗忘因子为1。则转速跟踪曲线如图2所示,参数估计曲线如图3所示。
由图2可以看出,本文所设计的JGPC控制器可以很好的跟踪给定速度曲线;且由辨识出的参数可知,本文第二节中提及的a约等于-0.983,b约等于0.27,这与由实际所用电机参数计算出的a,b一致,由此表明参数辨识的算法是可行的。
由图3传统GPC算法的仿真实验波形可以看出,采用改进GPC的PMSM驱动系统与传统的GPC驱动系统相比,其控制效果基本一致,但其计算较复杂,不利实际应用。因此本文采用的JPGC算法因其算法简单,且控制效果和传统GPC算法基本一致,故比于传统的GPC算法在PMSM控制系统中的应用更具有前景。
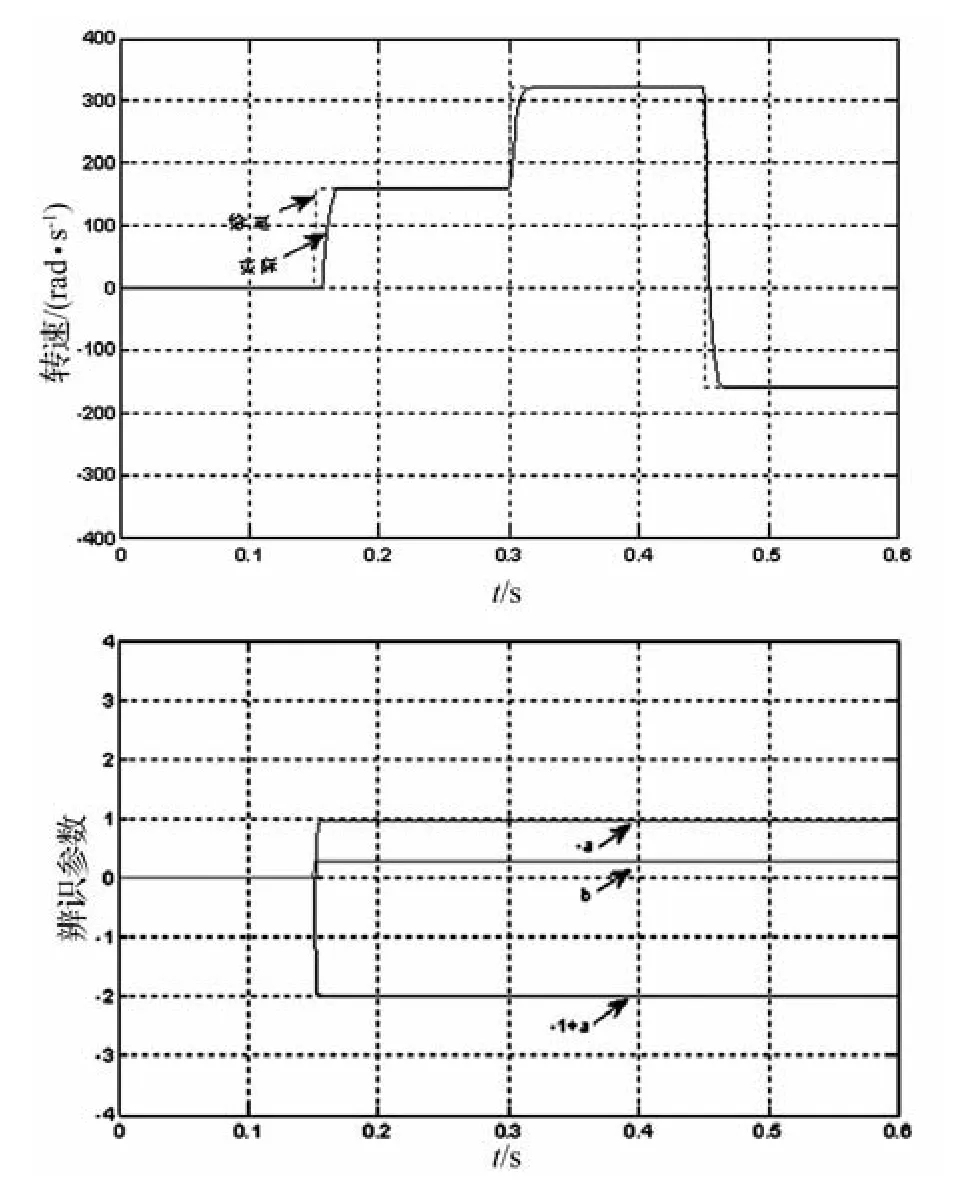
图2 采用改进GPC算法的转速跟踪及参数辨识曲线

图3 采用GPC算法的转速跟踪曲线
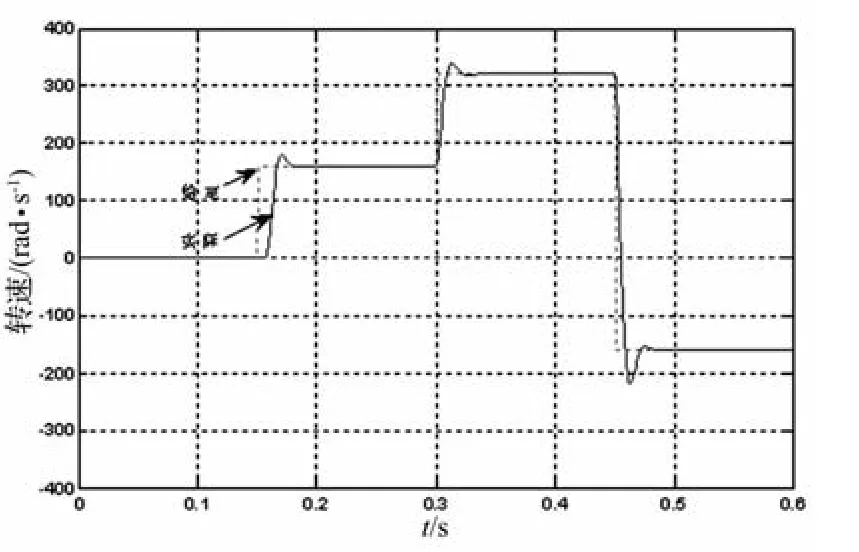
图4 采用传统PI控制器的转速跟踪曲线
由图4可以看出,采用传统的速度PI控制器的PMSM驱动系统具有一定的超调量,且快速性不如本文所介绍的采用改进的GPC控制算法的PMSM控制系统。实验结果表明,该控制算法在PMSM驱动系统中的是可行的,且比采用传统PI控制器更具优越性。
5 结束语
考虑传统广义预测控制器计算量较大,PI控制器鲁棒性不强且对于PI参数的设置经常需要依靠经验来不断尝试获得等缺点,本文采用一种改进的广义预测控制算法。理论上该控制算法可以保留传统GPC的主要优点,同时克服传统PI调节器的缺点。仿真实验表明,本文所设计的JGPC控制器可以很好的跟踪给定速度曲线,辨识出的参数跟实际电机的相关参数一致,且动态及稳态性能良好,达到了所预期的效果。
[1]杨承志,孙棣华,张长胜.系统辨识与自适应控制[M].重庆:重庆大学出版社,2009:69 -71.
[2]金元郁,顾兴源.改进的广义预测控制算法[J].信息与控制,1990,19.(3):8-14.
[3]庞中华,崔红.系统辨识与自适应控制[M].北京:北京航空航天大学出版社,2009:137-174.
[4]林瑞全,黄韬,王春迎.一种新型GPC算法及其在PMSM直接转矩控制中的实现[J].哈尔滨理工大学学报,2011,16(5):65 -71.
[5] Guoliang Wang,Hexu Sun,Lianbing Li.Applying Generalized Predictive Control to PM Synchronous Motor[C].Proceedings of the 5thWorld Congress on IntelligentControland Automation,Hangzhou,P.R.China, 2004
