极坐标导引头基于全像平面的盲区跟踪策略*

2014-09-20郭玉甫

弹箭与制导学报 2014年1期

郭玉甫，张平

（北京航空航天大学自动化科学与电气工程学院，北京 100191）

0 引言

滚仰式导引头结构紧凑，能大离轴角跟踪，是新一代近距格斗空空导弹的重要组成部分。但其小离轴角锥形盲区是由其结构导致的一个必须解决的问题。目前国内研究出的跟踪原理大都是采用根据目标在探测器位置与当前框架偏转角计算角度指令增量的方式。具体有较传统的根据运动学关系，通过光轴到视线的两种空间转动方式解算角度指令增量，其指令优化需要通过逻辑判断［1－2］;也有较先进的基于Paden-Kahan子问题求解角度指令增量，应用最小角增量准则对运动学逆解进行指令优化［3］。在这种指令架构下的过顶控制策略主要包括指令预测及分区域变参数控制策略［2，4］。由于探测器本身处在剧烈运动中，所以相较于角度指令增量，基于全像平面的指令计算与优化方式［5］得出的角度指令更适合进行动态规划和指令预测。文中在此指令方案的基础上改进了其中的坐标系旋转判据，并在分析目标运动模式的基础上设计了一种过顶跟踪策略。

1 坐标系定义

极坐标导引头外框滚转，内框俯仰，坐标系定义与目标成像几何关系如图1所示。图1中点o为两个框架轴的交点，f为o到探测器瞬时成像平面中心的距离。

载体基座坐标系oxbybzb（简称基座坐标系或载体坐标系）与稳定平台载体固连。经过绕x轴滚转后得外框坐标系oxoyozo，oxoyozo绕y轴俯仰后得内框坐标系oxpypzp。初始坐标系oxiyizi初始时刻与载体坐标系oxbybzb重合，其后坐标轴方向相对惯性空间保持不变，只随载体平移。在仿真中给目标运动提供惯性空间。

像球面是以点o为中心、探测器焦距f为半径的球面，目标与点o的连线与像球面交点称为目标的像点，光轴与像球面交点称为光点，可以分别用来表示目标视线与光轴位置。为更方便直观起见，以图1中oxb（xo）与像球面交点Q为中心将像球面展开成平面称为全像平面，进而可在全像平面上表示目标位置，并由此计算框架偏转指令。

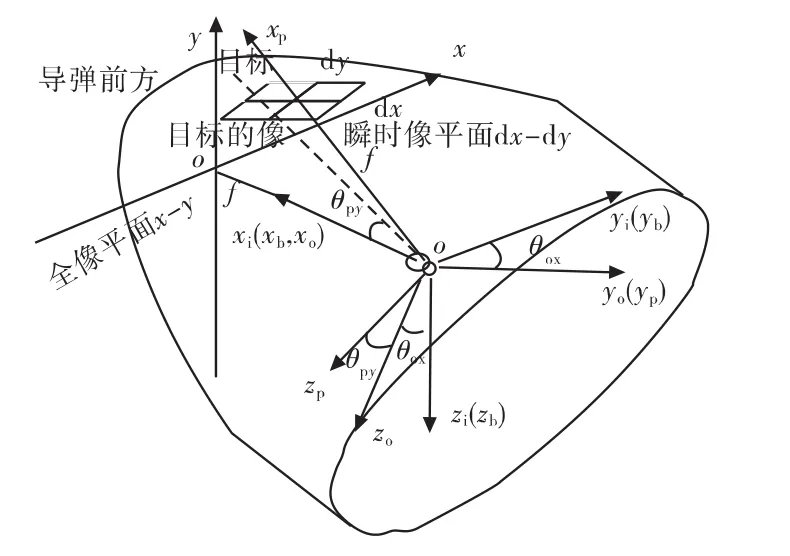
图1 坐标系定义

由图1可得，由载体坐标系三维坐标（xb，yb，zb）得到的全像平面二维坐标（x，y）为:

式（1）中，α、fβ分别为点在全像平面的极角（取值范围为－π/2～3π/2）与极径。β是点在载体坐标系的离轴角。对任一点p，其α，β角如图2所示。

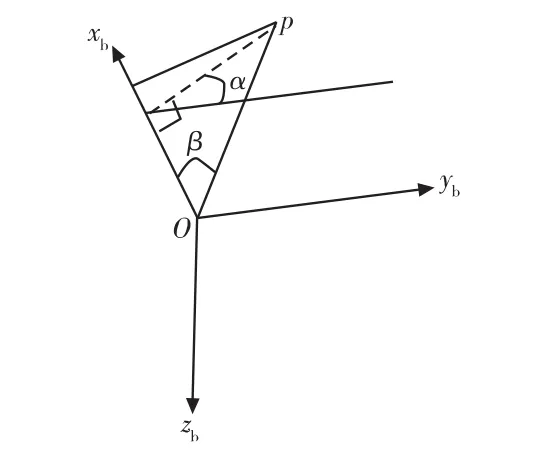
图2 载体坐标系上点的极角α与离轴角β示意图

2 指令计算与优化［5］

系统采取角度跟踪方式，由摄像头探测及图像处理得到的目标在瞬时像平面上的像点坐标（d x，d y），可直接构造像点在内框坐标系的坐标为（f，d x，－d y）。通过转换得到该点在载体坐标系坐标。再通过式（1）即可得目标对应的全像平面像点坐标（x，y），进而构造框架偏转指令。

2.1 初级指令公式

由图1中几何关系得框架偏转角度指令:

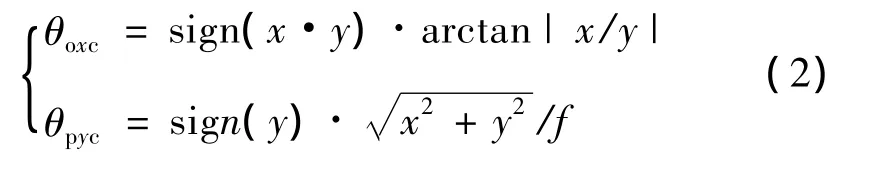
式中:θoxc和θpyc分别是外框滚转角和内框俯仰角指令（rad），下文各个角度都采用弧度单位;f是摄像头焦距（m）。

2.2 指令跳变与优化方式

从式（2）可以看出，当目标像点位于不同的象限，框架指令的符号不同，当像点跨越x轴时会出现指令正负符号的跳变，滚转指令跳变幅度约为π。以其中一种情况为例，如图3所示，当像点在x轴附近从第一象限运动到第三象限时，跨越前像点的滚转指令为α。当前像点的滚转角按式（2）计算为γ。显然大于π的角β才是合理的。得到角β的方式为将全像平面坐标系顺时针旋转π/2，在新坐标系下的坐标为:（x'，y'），且 x'= －y，y'=x则β =arctan|x'/y'|+π/2。

图3 指令跳变及旋转坐标系图示

由上述分析总结得指令优化的方式为:

当像点跨越x轴时将像平面的x、y坐标轴以原点为中心同时旋转+/－90°，旋转方向与像点跨越方向相同。最后再利用坐标系旋转公式对原来的目标像点坐标x和y进行转换，得到目标像点在旋转后坐标系下的坐标，对新坐标再按照式（2）计算滚转角和俯仰角指令，同时滚转角指令加上相应的π/2的整数倍得到最终的指令式（3）。

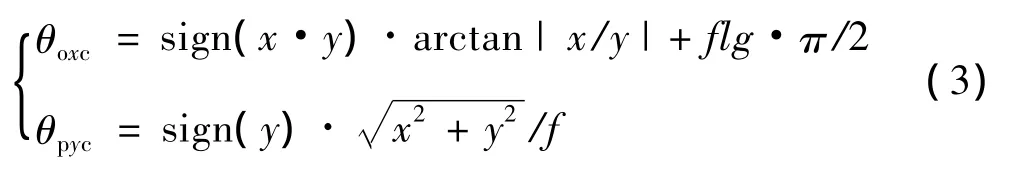
其中:（x，y）为坐标系旋转后的目标像点坐标，flg表示坐标系顺时针旋转次数。

2.3 原始的坐标系旋转判据

每个指令周期坐标系旋转的判据如表1、表2所示，当前像点坐标为（x，y），前一个像点坐标为（x0，y0）。

表1 顺时针旋转坐标系判据

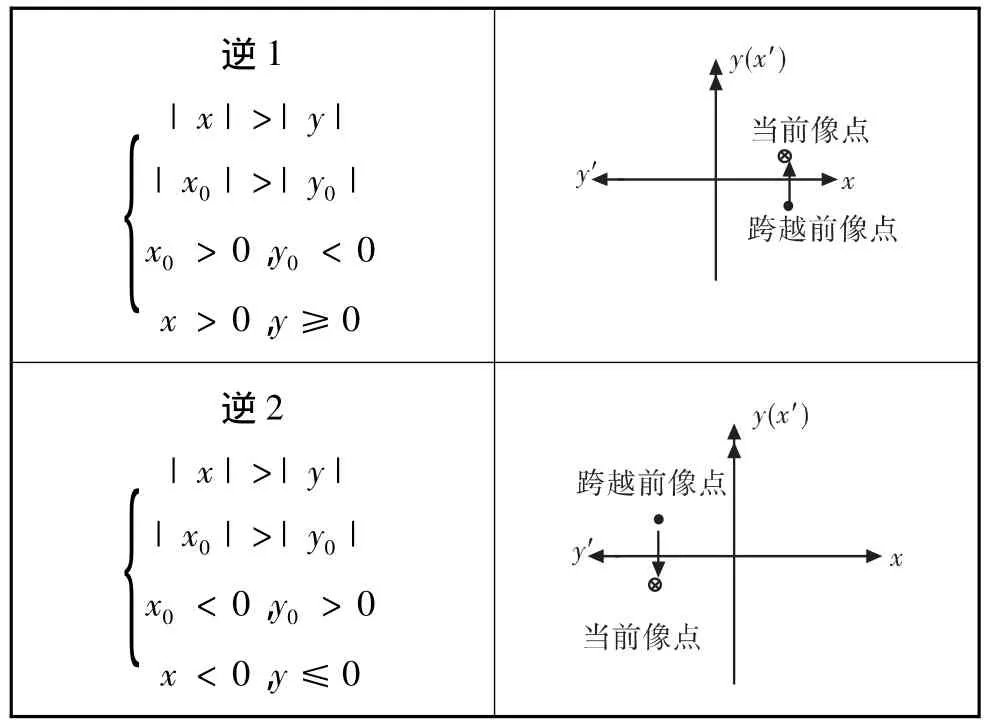
表2 逆时针旋转坐标系判据

3 盲区分析及目标运动模式分类

3.1 盲区分析

像球面上光点对像点的跟踪与光轴偏转角速度之间的关系如图4。

图4 像球面上光点运动示意图

为了分析光点对像点的跟踪，将当前像点在像球面上的移动速度分解为径向速度vr和切向速度vt。固定的目标视线运动角速率下，当目标视线运动对应的目标像点在像球面的速度全部为切向速度分量时，要求的滚转框滚转速度也最大，且这个要求的最大值随离轴角的减小在小离轴角区域急剧增加，导致过顶盲区的产生。因此，可给定最大目标视线角速率ωt，max，外框最大滚转角速度 ωox，max，可得能保证正常跟踪的最小离轴角θpy，min，也即盲区界定范围，如式（4）。

3.2 目标运动模式分类

1）目标运动模式1

运动描述:目标运动在盲区外。

由于外框所能提供的最大转速大于目标运动的要求，可实现正常跟踪。

2）目标运动模式2

运动描述:目标一直在盲区内运动。

由于盲区实质是体现小离轴角时框架能提供的像球面上光点切向速度的不足，因此最坏的情形即目标视线在盲区内以最大角速度绕外框滚转轴作旋转运动，其运动的离轴角记为α。

可以想见，这种情况下外框以极速偏转，但滚转角跟踪误差线性增加，然而失调角却会从0到峰值作周期运动。失调角峰值产生于当光轴，目标视线和外框滚转轴共面时，其值为2α，如图5所示。

图5 目标盲区内圆周运动最大失调角示意图

所以目标运动情形2下的失调角≤2θpy，min，即2倍的盲区边界离轴角。在此情况下若要保证目标不丢失，则探测器的探测角要 ≥2θpy，min。

3）目标运动模式3

运动描述:目标从盲区外进入盲区内再出来，即目标对盲区的穿越。

该运动模式体现了极坐标导引头的奇异性［2］，目标进入盲区后，一开始外框跟踪不上产生一定的外框跟踪误差，但在小离轴角盲区内此误差并不会导致大的失调角。随着目标视线的离轴角增大，如外框跟踪误差不能尽快消除，则会产生大的失调角，当失调角超出探测器探测范围时就会形成目标丢失。

4 坐标系旋转判据改进及盲区策略设计

由上节分析可知只有目标运动模式3才会导致目标丢失，根据其特点可设计指令策略如下:当目标在指定范围的小离轴角区域运动时，若目标像点的极角变化过快，就使滚转角指令保持不变，并记录进入滚转保持策略前的最后一个点，当策略执行条件不成立时，将最后一个点坐标看作上一个点坐标，并作为指令计算与优化的依据来形成指令。仿真表明，目标快速穿越盲区，可导致正常跟踪丢失时（设探测器瞬时视场大小为±3°），若使用上述策略，将会产生外框保持几个周期而后反向滚装，同时内框变号的指令，可达到以较小的外框滚转角速度跟踪目标的目的，仿真表明这种情况下可有效降低跟踪过程中的最大失调角。

4.1 旋转坐标系判据改进

为保证在目标快速穿越盲区运动中，滚转保持策略可以最终实现滚转框的反向偏转，且不论这种穿越以何种方向。需将2节中指令优化的坐标系旋转判据作两点改进:

1）将判据中判定需旋转坐标系的x轴两侧扇形区缩小;

2）将判据调整为对坐标系的 x轴、y轴功能对称。

改进后坐标系旋转判据如表3～表4所示，当前像点坐标为（x，y），前一个像点坐标为（x0，y0），～表示非。

k用以完成改进1），可根据导引头参数和要达到的目标视线跟踪速率指标取值，在下面仿真中取为3。顺3，顺4，逆3，逆4 完成改进2）。

4.2 滚转保持策略描述

加入策略后指令模块输入输出如图6所示。

输出:thto xc，thtp yc为角度指令。（x last，y last）为执行策略前的最后一个目标像点全像平面坐标。s_flg表示该周期是否执行了策略，1表示是，0表示否。flg如前所述，表示全像平面坐标系顺时针旋转π/2的次数。

输入:经延迟模块得到的都是指相应变量的上一个周期值，后加0 来表示，如 s_flg0，flg0，x last0，y last0，thto xc0。（x，y）、（x0，y0）分别是目标像点的当前坐标和上一个周期的坐标。

指令计算与优化过程如图7。

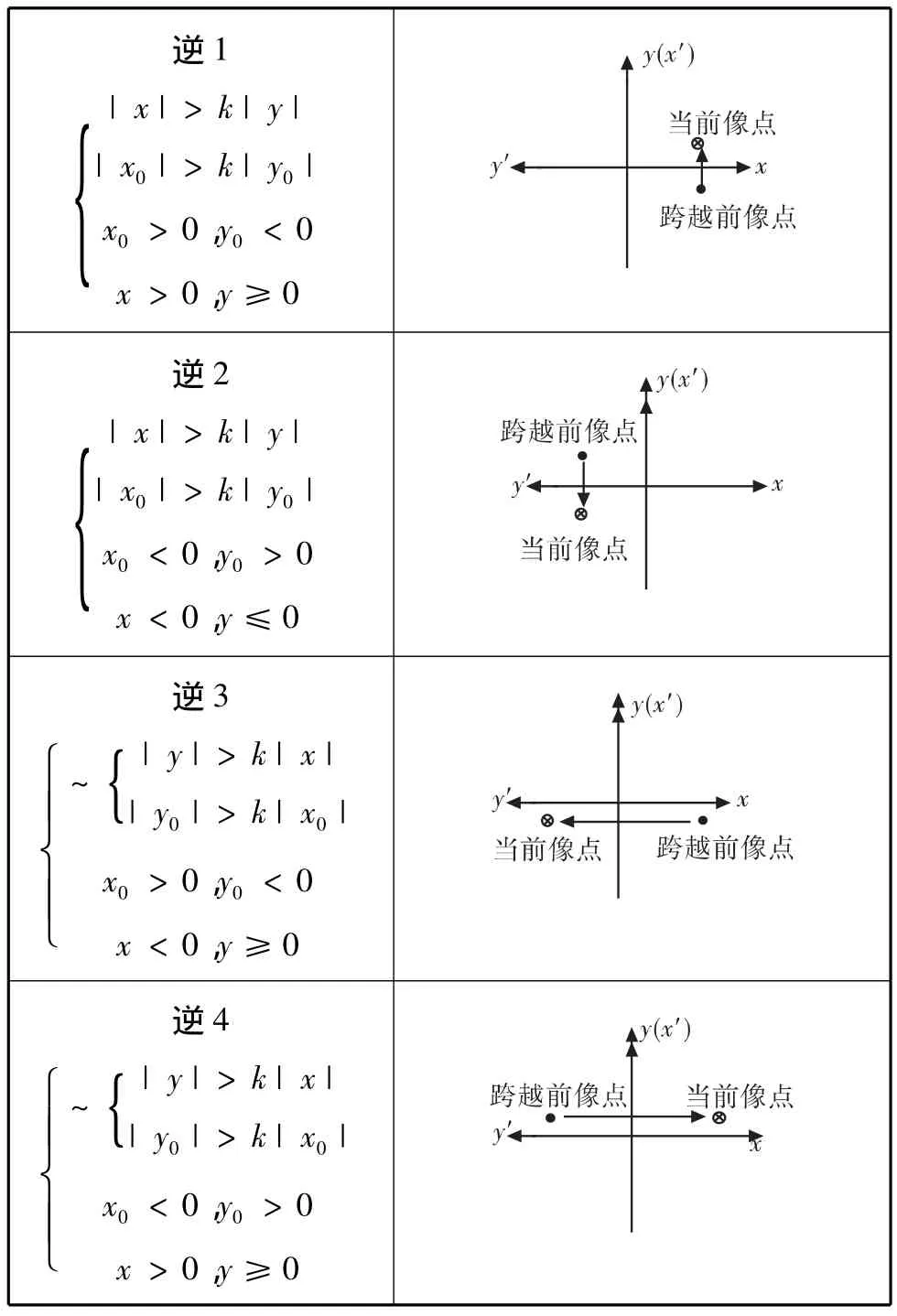
表4 改进的逆时针旋转坐标系（逆3、逆4为新增）

图6 采用滚转保持策略的指令计算与优化函数输入输出示意图

图7 带策略指令计算与优化过程

其中R为策略区大小，应取稍小于式（4）所计算出的盲区范围。r01为当前像点与上一个像点的距离:，条件中加入其大于某阈值的作用是当目标视线在小离轴角策略区运动较慢时，使系统正常跟踪，从而不影响视线稳定，使跟踪保持小的失调角。alpha01为当前像点与上一个像点的极角差，如图8所示。直接计算其余弦值为:标记该周期是否应用了策略，为下一周期提供判断依据，辅助实现策略。

图8 alpha01示意图

图9 目标运动模式3轨迹

5 仿真结果及分析

5.1 目标轨迹与模型参数

此处仿真针对目标运动模式3，目标轨迹在xb=1平面给出，采用目标匀速直线穿越盲区的形式，如图9。

目标轨迹如图所示，运动方向竖直向下，目标像点速度v根据跟踪指标最大目标视线角速率30°/s取为 π/6，α 取为0.3°。

导引头外框最大滚转角速度:1000°/s。

5.2 仿真结果

1）普通跟踪

图10 普通跟踪框架指令

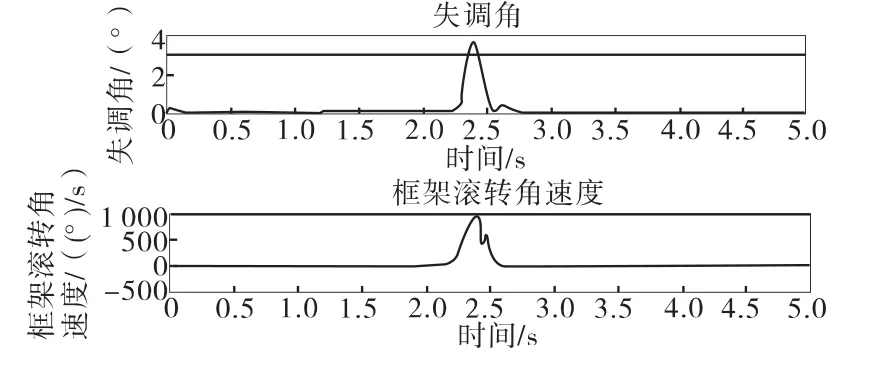
图11 普通跟踪失调角及外框滚转角速度

2）策略跟踪

仿真中，取 R=f·0.6·π/180 ，0.6°为设置的策略区边界离轴角。

5.3 仿真结果分析

图10显示，由于极坐标导引头的小离轴角盲区滚转指令的奇异性，正常跟踪时滚转框角度指令有个短时间内的近似π的阶跃，这导致实际滚转框产生较大的跟踪误差，在目标视线离轴角增大后，这个误差不能及时消除，导致了较大的跟踪失调角。图11显示最大失调角大于3°，在实际情况中就会导致目标丢失，视线闭环不能维持。图12显示应用策略后，实现了滚转框的反转，同时俯仰框变号，图13显示这种情况使得跟踪失调角的最大值减小到小于1.5°，即目标不会丢失。