3-(2SPS)并联机构灵巧度分析
2014-09-19刘宁宁李开明
刘宁宁,李开明
(南京理工大学机械工程学院,江苏南京210094)
0 前言
并联机构的灵巧度是衡量输入与输出运动(力)之间传递精度、评价机构运动学性能的一个重要指标,也是尺度参数设计的重要依据[1-2]。通常情况下,雅克比矩阵的条件数是评价并联机构灵巧度的常用指标。Salisbury指出当雅克比矩阵的条件数达到1时,并联机构是各向同性的。
3-(2SPS)并联机构是 Stewart机构的一种变形,具有3个移动自由度。运动学正、反解唯一,且具有相当好的力学性能,承载能力较强,适用于载荷较大工况条件。本文根据3-(2SPS)并联机构的结构布局和特点,建立其运动学方程,并得到力雅克比矩阵,以雅克比矩阵的条件数来分析机构的灵巧度,然后利用MATLAB软件进行仿真并分析,为并联机床结构优化与设计提供理论依据。
1 3-(2SPS)并联机构及其运动学
3-(2SPS)并联机构简图如图1所示,该并联机构通过六条两两平行的滚柱丝杠连接上下两平台,即A1B1//A2B2,A3B3//A4B4,A5B5//A6B6。 其中下平台固定,上平台可进行平动,机构通过特殊的铰链布置和伸缩杆同步驱动限制了末端执行器的三个转动自由度,机构可以实现三个移动自由度。

图1 3-(2SPS)并联机构简图
首先建立坐标系如图1所示,固定坐标系O-xyz固联于下平台,坐标中心O与下平台几何中心重合,动坐标系O'-x'y'z'固联于上平台,坐标中心O'与上平台几何中心重合。 其中Ox轴(Ox'轴)过B1B2(A1A2)中点,Oz轴(Oz'轴)垂直向上。定平台与动平台的外接圆半径分别是R和r,且 R ﹥ r。
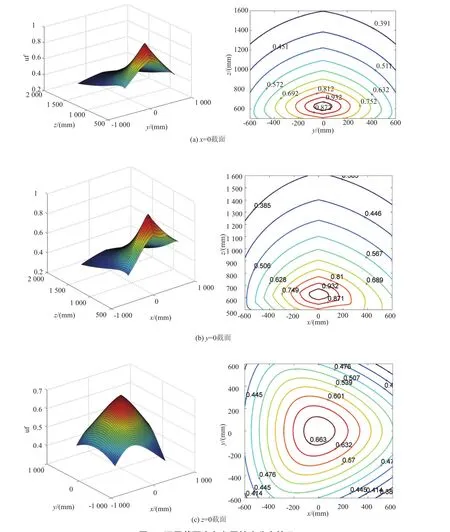
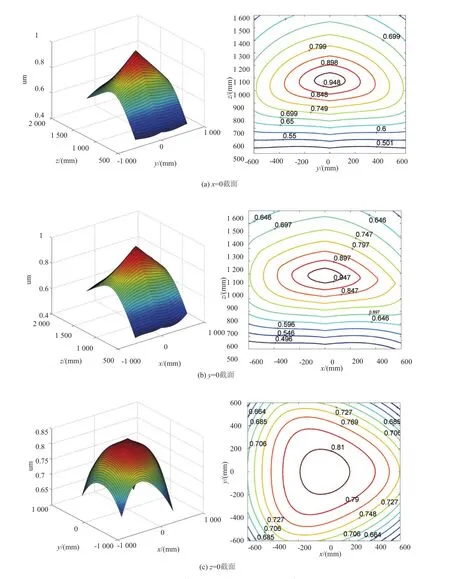
图2为定平台和动平台在xoy平面投影的铰链点间的几何关系。其中d为定平台(动平台)上两根平行驱动杆的铰链点间距。d的大小由动平台外接圆半径及驱动杆决定,设d0为平行杆发生干涉的临界距离,则d0 根据图2,可以求出定平台各铰链点相对于定坐标系的坐标和动平台各铰链点相对于动坐标系的坐标,然后设动坐标系原点O'在定坐标系中的坐标为,经过坐标变换即可求得杆长,由于本文的研究对象为三自由度平动机构,则继而可以得到机构驱动杆的杆长为: 图2 定、动平台在xoy平面的投影 其中:μ=H-h。 对式(1)求一阶偏导数,得到该机构的三阶速度雅克比矩阵,由雅克比矩阵可以证明在机构的工作空间内不存在奇异位姿[4]。在不考虑关节之间的摩擦力等影响因素的情况下,将速度(运动)雅克比矩阵转置即可得到机构的力雅克比矩阵[5],可以得: 其中: 雅克比矩阵实质反应的是机构末端输出运动与驱动输入运动之间的速度比。从机构的操作和控制的精度出发,当机构处于奇异位形或接近奇异位形时,雅克比矩阵会呈现病态,此时机构输入与输出之间的运动传递会出现失真,而灵巧度就是衡量失真程度的指标[6]。描述机构运动的灵活性可用雅克比矩阵的奇异值构造灵巧度评价指标,如条件数、最小奇异值、可操作性等[7]。本文采用雅克比矩阵条件数进行灵巧度分析。 矩阵条件数、矩阵最大奇异值与最小奇异值之间存在如下关系: 由此可知cond(G)≥1,矩阵条件数越接近1,矩阵性态越好。条件数越大,矩阵越趋于病态,机构的输入输出之间的运动传递会出现较大的失真。当条件数为1时,机构的各个方向放大倍数都相等,机构运动学处于各向同性。因此在进行机构设计和控制时,要尽量使雅克比矩阵各向同性,以得到较好的机构性能。 为了更好地分析机构的灵巧度,本文将动平台的力雅克比矩阵分为力映射矩阵和力矩映射矩阵的形式: 为了分析方便,取映射矩阵的条件数的倒数来衡量动平台的各向同性度:其中:uF为力各向同性度,uM为力矩各向同性度。 已知3-(2SPS)并联机构动平台外接圆半径为202 mm,定平台外接圆半径为1 000 mm,平行杆铰链点安装距离为350 mm。 借助MATLAB软件编程仿真可以得到并联机构的力各向同性和力矩各向同性的分布图。图3为在x=0、y=0、z=0的三个截面得到的力各向同性度。 图3 不同截面力各向同性度分布情况 由图3(a)可知,在x=0截面内,力各向同性度关于y=0对称,且随着y值的增大而减小;z增大,在一定范围内,力各向同性度也会减小。图3(b)反应了类似的情况,力各向同性度大致关于x=0对称,且随着x的增大而减小;z增大,在一定范围内,力各向同性度也会减小。图3(c)中,在z=0截面,力各向同性度关于y=0对称,且随着y值的增大而减小,x增大,力各向同性度也会减小,在z=0截面内,力各向同性度较差。 与力各向同性度分析方法类似,分别可以得到在x=0、y=0、z=0的三个截面得到的力距各向同性度,如图4所示。 图4 不同截面力距各向同性度分布情况 由图4(a)可知,在x=0截面内,力距各向同性度关于y=0对称,且随着 y值的增大而减小;当 z大致在1 100 mm时,力矩各向同性度最大,表现为灵活性最好。图3(b)反应了类似的情况,力距各向同性度关于x=0对称,且随着x的增大而减小;当z大致在1 100 mm时,力矩各向同性度最大。图3(c)中,在z=0截面,力距各向同性度关于y=0对称,且随着y值的增大而减小,x增大,力距各向同性度也会减小,在z=0截面内,力距各向同性度较差。 根据3-(2SPS)并联机构的结构布局和特点,建立运动学方程,得到力雅克比矩阵。以机构的雅克比矩阵的条件数评价并联机构的灵巧度。运用MATLAB软件得到并联机构的力各向同性和力矩各向同性的分布图,经分析得出当机构处于x=0,y=0时的各向同性度最好,机构的灵巧度最好。研究结果可为并联机床设计提供理论参考。 [1]黄田,王劲松.Stewart并联机器人局部灵活度与各项同性条件解析[J].机械工程学报,1999,35(5):41-46. [2]金振林,高峰.一种正交并联机器人的灵巧度指标及分布[J].机械设计,2001,18(7):19-22. [3]乐林林,李开明.3-(2SPS)并联机构静刚度分析[J].现代设计与先进制造技术,2010,39(5):39-43. [4]李琳,李开明.新型三平动并联机床的运动分析[J].机械制造与自动化,2013,41(1):12-15. [5]黄真,赵永生,赵铁生.高等空间机构学[M].北京:高等教育出版社,2006.6. [6]张彦裴.一种冗余输入并联机器人研究[D].河北工业大学.2003. [7]陈修龙,赵永生,鹿玲.并联机床的灵巧度评价指标及其应用[J].光学 精密工程,2007,15(2):237-242.



2 条件数与灵巧度



3 具体分析
4 结论
