平面向量中不得不提的一个恒等式

●单长松 (浙江师范大学数理与信息工程学院教育硕士 浙江金华 321004)

平面向量中不得不提的一个恒等式

●单长松 (浙江师范大学数理与信息工程学院教育硕士 浙江金华 321004)

高中数学中存在着大量等量关系，如立方差(和)公式、二项展开式、两角和与差公式等.在高中数学中常能见到这些等量关系的身影，这也是高中教学重点关注的对象.但有些等量关系看似冷门甚至课本上都不出现，但它在问题解决过程中却能起到立竿见影的效果，实现对问题的快速“秒杀”.

1 极化恒等式

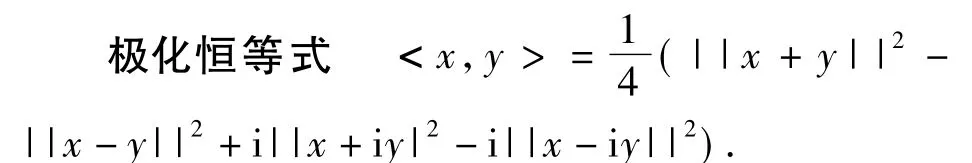
图1

极化恒等式最初出现于高等数学中的泛函分析，它表示数量积可以由它诱导出的范数来表示.把这个极化恒等式降维至二维平面得

2 极化恒等式的应用

自向量引入高中数学以后，由于它独特的性质(代数与几何的桥梁)，在近几年全国各地的高考中迅速成为创新题命制的出发点，在浙江省数学高考中尤为突出，也出现了一些非常精美的向量题.

这个问题的本质就是极化恒等式.

下面我们再来看2013年浙江省数学高考选择题第7题：

(2013年浙江省数学高考理科试题)

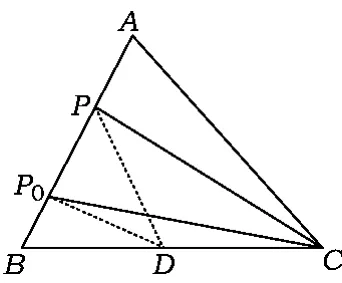
图2

分析如图2，取 BC的中点 D，联结 PD，P0D，在△PBC内使用极化恒等式得在△P0BC内使用极化恒等式得

由条件知恒有PD≥P0D，即P0D⊥AB，故AC=BC.

很多一线教师都认为这个题目在10个选择题中是最难的，应该放在压轴的位置.笔者却不这样认为，其实这个题目只是在例1的基础上对极化恒等式的应用灵活化，步子迈得更大一些而已.这个题目的姊妹题也出现在2013年浙江省高中数学联赛中.

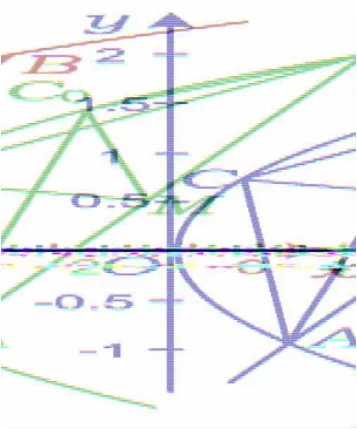
图3

例3如图3，已知直线AB与抛物线y2=4x交于点A，B，M 为 AB 的中点，C 为抛物线上一个动点，若C0满足则下列一定成立的是( ).

A.C0M⊥AB

B.C0M⊥l，其中l是抛物线过点C0的切线

C.C0A⊥C0B

即抛物线y2=4x上所有点到M的距离最近的点即为C0，故以M为圆心、MC0为半径的圆与抛物线内切.故选B.

除此之外，还有许多优秀的题目.

例4设正方形ABCD的边长为4，动点P在以AB为直径的圆弧上(如图4所示)，则的取值范围是 .

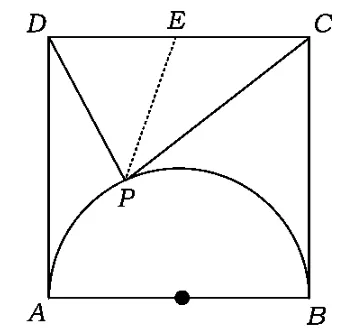
图4

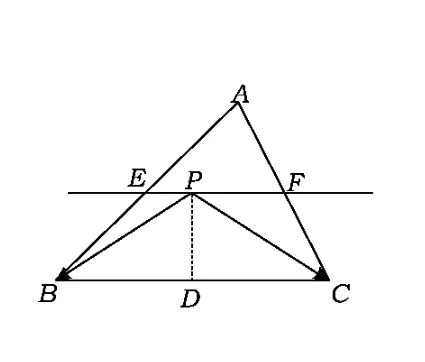
图5

分析取CD中点E，联结PE，在△PDC内使用极化恒等式得

3 极化恒等式带来的反思

(1)极化恒等式源于教材又高于教材.在△ABC中，

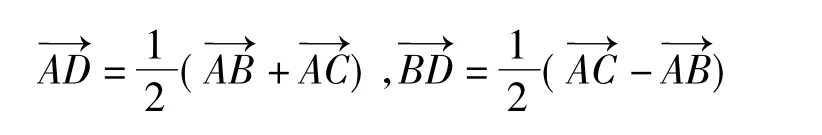
是课本上出现的2个重要的向量三角关系，而极化恒等式无非就是这2个公式的逆用.

(2)具有三角几何背景的数学问题利用极化恒等式考虑尤为简单，让“秒杀向量”成为另一种可能.

(3)向量是连接代数与几何的桥梁，由于向量的坐标运算引入，向量与代数的互换运算可以说是深入人心，而与几何的运算联系略显单薄.而极化恒等式恰恰弥补了这个缺憾，可以说极化恒等式应该是把向量的数量积问题用形象的几何图形展示得淋漓尽致.