可换半群作用下的n 敏感

曾眺英

(嘉应学院 数学学院，广东 梅州 514015)

0 引言

设X 是以d 为其度量的紧致度量空间，f，g：X→X 为可换的连续映射，即gof=fog.令

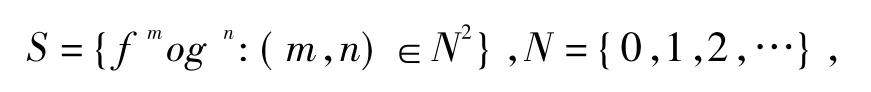
则S 关于映射的复合构成一个可换的幺半群，并且关于其上的离散拓扑(S，o)是一个有有限生成元(f，g，IdX)的拓扑半群.以(X，S)表示由S 在空间X上的作用所定义的动力系统.

在N2上定义加法运算，(m，n)+(p，q)=(m+p，n+q)，那么(N2，+)是一个关于离散拓扑的拓扑群，并且(N2，+)与(S，o)同构.

假设(X，S)是一个动力系统，其中X 是一个完备度量空间，S={fmgn：(m，n)∈N2}，f，g：X→X 为X 上的可换连续自映射.易见ρ：(X×X)×(X×X)→R+，ρ((x，y)，(u，v))=max{d(x，u)，d(y，v)}为X×X 上的一个完备度量.此外，对于任意(m，n)∈N2，由可换映射f，g：X→X 诱导了X×X 上的连续自映射(fmogn)×(fmogn)：X×X→X×X，其定义如下：

((fmogn)×(fmogn))(x，y)=(fmogn(x)，(fmogn(y)).在集合S⊗S：={(fmogn)×(fmogn)：(m，n)∈N2}上规定乘法“*”如下：((fmogn)×(fmogn))*((fpogq)×(fm+pogn+q)×fm).易见S⊗S，仍然是一个幺半群.将S⊗S 在X×X 上的作用定义的动力系统简记为(X×X，S⊗S).

动力系统中的n 初值敏感的概念是熊金城教授在文献［1］提出的.对给定的整数n≥2，系统(X，T)称为n 初值敏感的是指，存在ε＞0，使得对任意非空开集U 均存在互异的点x1，x2，…，xn∈U 和自然数m∈N 满足min{d(Tmxi，Tmxj)：1≤i≠j≤n}≥ε.这样的ε＞0 称为系统(X，T)的一个n 初值敏感常数.

用Furstenberg 族的语言探讨拓扑动力系统是近年来的热点问题.族的概念最早可追溯到在一般拓扑学与数理逻辑中滤子的使用，但这种用族的观点来研究系统动力学性质的思想首先在1955 年由Gottschalk 和Hedlund 引入的.之后许多数学工作者沿着这一思想进行了有意义的讨论.但真正得到发扬光大的是Furstenberg 及其合作者，他在其经典著作［2］中将这一思想进行了深刻而又漂亮的阐述，他的工作将拓扑动力系统与遍历理论的应用深刻置入组合数论与Ramsey 理论之中，对相应的数学分支有着广泛而深远的影响.在最近的几十年，Furstenberg 的追随者根据这一想法在各个相关领域进行了富有成效的研究.文献［3］用族语言探讨了n初值敏感性，并得到了一些基本性质.

本文尝试利用Furstenberg 族的语言，讨论在可换半群作用下的n 初值敏感性.Furstenberg 族的相关基础知识，详情请参见文献［4］.

1 预备知识

设S 为自然数集的笛卡儿积N2的所有子集构成的集合.ℓ⊂S 称为一个Furstenberg 族，如果它是向上遗传的，即若F1⊂F2并且F1∈ℓ，则F2∈ℓ.一个Furstenberg 族ℓ 是一个常义Furstenberg 族当∅∈ℓ 且N2∈ℓ 仅当∅∈p 且N2∈p.Furstenberg 族的对偶族定义为：

κℓ={F∈S：N2-F∉ℓ}={F∈S：F∩F'≠Ø，对于所有F'∈ℓ 成立}.易见，它也是一个族.若ℓ为常义族，则κℓ 也是常义族.如果F，F1和F2都是常义族，则有κ(kF)=F，并且F1⊂F2蕴涵κF2⊂κF1.ℓ1与ℓ2的乘积ℓ1·ℓ2定义如下：ℓ1·ℓ2={F1∩F2：F1∈ℓ1，F2∈ℓ2}.以β 表示由N2的所有无限子集构成的族，则β 是一个Furstenberg 族，并且其对偶族κβ 是所有余有限集所构成的族.一个Furstenberg 族F 称为满的，如果它为常义族并且满足κℓ·ℓ⊂β.

对于U，V⊂X，记Nf，g(U，V)={(m，n)：(fmgnU)∩V≠Ø}，称为集合U 和V 的碰撞时间集.特别地，当U 是某独点集{x}，我们简单地记Nf，g({x}，V)为Nf，g(x，V)，并且称之为点x 在集合V 中的回复时间集.

对于A，B⊂X，定义d(A，B)=inf{d(a，b)：a∈B}.当A={a}时，以d(a，B)表示d(A，B).∀δ＞0和X 的任意子集A，记［A］δ={x∈X：dust(x，A)＜δ}，其中dist(x，A)=inf{d(x，y)：y∈A}.并且△δ={x，y}∈X2：d(x，y＜δ)，易知，

称点x 为集合A 的一个ℓ-贴附点，如果点x在集合A 中的回复时间集属于ℓ，即N(x，A)∈ℓ.集合A 的所有ℓ-贴附点x 构成的集合，记作ℓ(A，S)，称之为集合A 的ℓ(A，S)贴附集.明显地有：ℓ称Furstenberg 族ℓ 是与系统(X，T)兼容的［5］，如果每一个开集U⊂X 的ℓ-贴附集ℓ(U，T)是一个Gδ集.

设ℓ⊂β 是一个族，称系统(X，T)为ℓ 传递的，是指对X 的任意非空开集U，V，N(U，V)∈ℓ 成立.如果存在点x∈X，使得对X 的任意非空开集U，均有N(x，U)∈ℓ，则称点x 为系统(X，T)的一个ℓ 传递点，X 的全体传递点记为Transℓ(X，T).

2 主要结果

定义［3］ℓ⊂β，对于取定的自然数n≥2，系统(X，T)称为ℓ-n-初值敏感的是指，存在ε＞0，使得对任意非空开集U 均存在n 个互异的点x1，x2，…，xn∈U 满足{m∈Z+：min{d(Tm(xi)，Tm(xj))：1≤i≠j≤n}＞ε}∈ℓ.这样的ε＞0 称为系统(X，T)的一个ℓ-n-初值敏感常数.

定义1ℓ⊂β，对于取定的自然数n≥2，系统(X，T)称为ℓ-ε-n 初值敏感的是指，存在ε＞0，使得对任意非空开集U 均存在n 个互异的点x1，x2，…，xn∈U 满足{(m，n)∈N2：min{d(fmgn(xi)，fmgn(xj))：1≤i≠j≤n}＞ε}∈ℓ.这样的ε＞0 称为系统(X，T)的一个ℓ-ε-n 初值敏感常数.

设π：X→Y 为连续映射，如果X 的非空开集在π 下的像集具有非空内部，则称π 为半开的.下面说明，在可换半群作用下的ℓ-ε-n 初值敏感可以被因子映射所提升.

命题1ℓ ⊂β，设(X，T)和(Y，S)是两个拓扑动力系统且因子映射π：X→Y 是半开的.如果(Y，S)是ℓ-ε-n 初值敏感的(n≥2)，那么(X，T)也是ℓ-ε-n 初值敏感的.

证明设ε＞0 是(Y，S)的ℓ-ε-n 敏感常数.由π 的连续性知：若d(y1，y2)＞ε 且π(xi)=yi，i=1，2，则存在ε＞0 使d(x1，x2)＞ε.

设U 是X 的任意非空开集，由于π 是半开的，则π(U)包含了一个Y 的非空开子集V.于是对于ε＞0，存在n 个不同的点y1，…，yn∈V，使得：A=≠j≤n}＞ε'}.选取x1，…，xn∈U 且π(xi)=(yj)，1≤i≤n，则，即系统(X，T)是ℓ-ε-n 初值敏感的.

命题2设π：X→Y 为系统(X，T)到(Y，S)的因子映射，且是一个常义族，则

(1)如果(X，T)是ℓ 传递的，那么(Y，S)也是ℓ传递的；

(2)如果(X，T)的ℓ 传递点集非空，则(Y，S)的ℓ 传递点集也非空，且

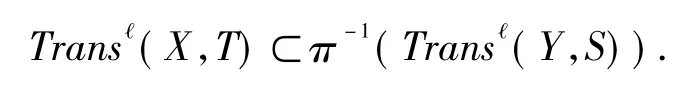
证明(1)任给Y 中的非空开集U，V，π-1U，π-1V 是X 中的非空开集，由条件知：N(π-1U，π-1V)∈ℓ，且A={(m，n)∈N2：(π-1U)∩(T2-nT1-m(π-1V))≠∅}∈ℓ，因为oπ，得(V))≠∅}=A∈ℓ，由于π 是满射，有

∈ℓ，即(Y，S)也是ℓ 传递的.

(2)设x 为X 的ℓ 传递点，V 为Y 的任意非空开集，则π-1V 为X 中的非空开集.由条件，对于系统(X，T)有：N(x，π-1V)∈ℓ，由于，得N(π(x)，V)∈ℓ：对于系统(Y，S)成立.

定理设ℓ 是与系统(X，S)兼容的Furstenberg族，并且κℓ 是可数生成的，若存在ε＞0，使得系统是ℓ-ε-n 初值敏感的，则集合X2-ℓ(X2-是第一纲的Fσ集.

证明设г 是κℓ 的可数生成元，则

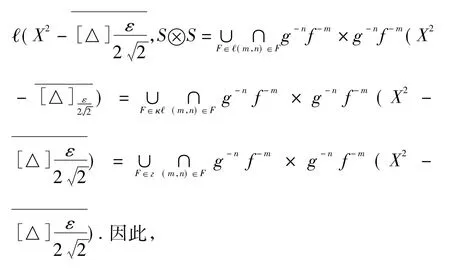
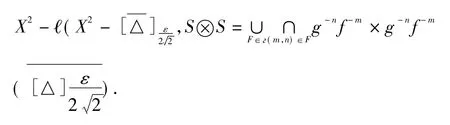
下证：任意F∈ℓ，

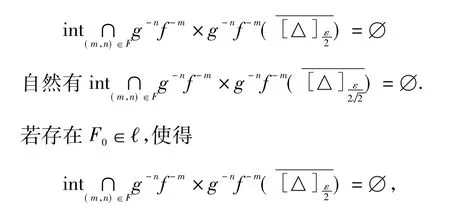
即存在(x，y)∈X2，和λ＞0，使得

对于任意(z1，…，zn)∈B(x，λ)和(m，n)∈N2，因为

(⊃F0∈г ⊂κℓ.故因此对任意(z1，…，zn)∈B(x，λ)，NS⊗S((z1，…，zn)，

这与S 是ℓ-ε-n 初值敏感矛盾，定理得证.