双层钢板-内填混凝土组合剪力墙滞回性能数值分析*

罗永峰, 李 健, 郭小农

(同济大学 建筑工程系，上海 200092)

剪力墙结构因其抗侧刚度大，能有效减少楼层水平位移，自20世纪60年代起，被广泛应用于高层及高耸结构中.剪力墙可根据建造材料分为钢筋混凝土剪力墙、钢板剪力墙及组合剪力墙.

组合剪力墙是将2种以上的材料通过某种形式组合在一起形成剪力墙，可抵抗竖向力和水平力，材料通常为钢和混凝土2种.剪力墙的混凝土与钢结构之间通过设置构造措施使之协同工作.根据构造形式的不同可分为带边框和不带边框的组合剪力墙；根据钢板所在位置又可分为内嵌钢板-外包混凝土式、单侧钢板-混凝土式、双层钢板-混凝土式等[1].本文所研究的双层钢板内填混凝土组合剪力墙就属于不带边框的双层钢板-混凝土式.

目前，国内外学者对双层钢板内填混凝土剪力墙研究较少.Wright等[2-3]对双面压型钢板内填混凝土组合剪力墙在施工阶段和使用阶段的轴压性能和抗剪性能进行了试验研究，由于采用的压型钢板较薄，容易失稳，使得钢板屈曲对这种剪力墙抗剪性能有较大影响.Eom等[4]对内设纵横向加劲肋的双层钢板组合剪力墙进行了往复水平荷载作用下的试验研究，试验中支座约束形式对试件的受力性能有较大影响，并影响了最后的破坏模式.聂建国等[5]为了优化高层结构中的剪力墙，对两边带端柱的双层钢板组合剪力墙进行了抗震性能试验研究，得到了滞回性能曲线、延性系数、典型的破坏形态等.Link等[6]对双层钢板内填混凝土组合剪力墙在竖向荷载和水平反复荷载下的极限承载力和后期承载力进行了非线性有限元分析.Corus[7]公司提出Bi-steel组合墙构造并开展了相应的研究.司波等[8]利用有限元软件对双层钢板剪力墙钢板厚度、墙的高厚比、边长比等对其抗侧刚度的影响进行分析，并利用单位荷载法对抗侧刚度进行拟合.黄会平等[9]以千手观音实际工程为背景，用有限元软件分析了双层钢板剪力墙抗剪屈曲性能，得到了其基本承载力.祝文君等[10]在黄会平研究的基础上，对双层钢板剪力墙进行了滞回性能数值分析.

虽然双层钢板内填混凝土剪力墙具有良好的抗震性能，但由于它是一种新型的结构形式，相应的试验研究、理论研究和设计方法较少，还没有形成完整

的体系.目前尚需研究的主要问题有：1)不同构造形式对其承载力和延性的影响；2)不同钢板强度和混凝土强度对其承载能力的影响；3)轴压比对其滞回性能的影响；4)剪力墙高厚比、宽厚比等参数对其抗震性能的影响；5)剪力墙的简化设计方法；6)剪力墙在施工过程中的力学性态等.

本文在已有试验研究的基础上，分析双层钢板内填混凝土剪力墙试件的受力特点，建立考虑剪力墙初始几何缺陷的有限元模型，在与试验结果对比分析的基础上，通过大量数值分析，研究主要参数对剪力墙受力性能的影响特征与规律，为双层钢板内填混凝土剪力墙的深入研究与应用提供数据和资料.

1 试验简介

1.1 试验设计

设计了9个双层钢板内填混凝土组合剪力墙试件，试件缩尺比例为1∶2.5.试件钢板材料为Q235，混凝土有C30和C50两种.根据工程实际选取两种轴压比0.4和0.25.试件设计图如图1所示，试件参数见表1.

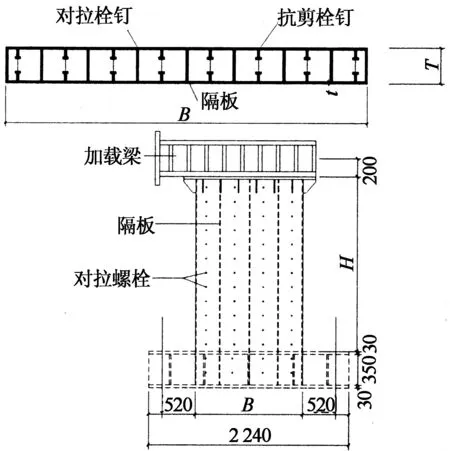
图1 试件设计示意图

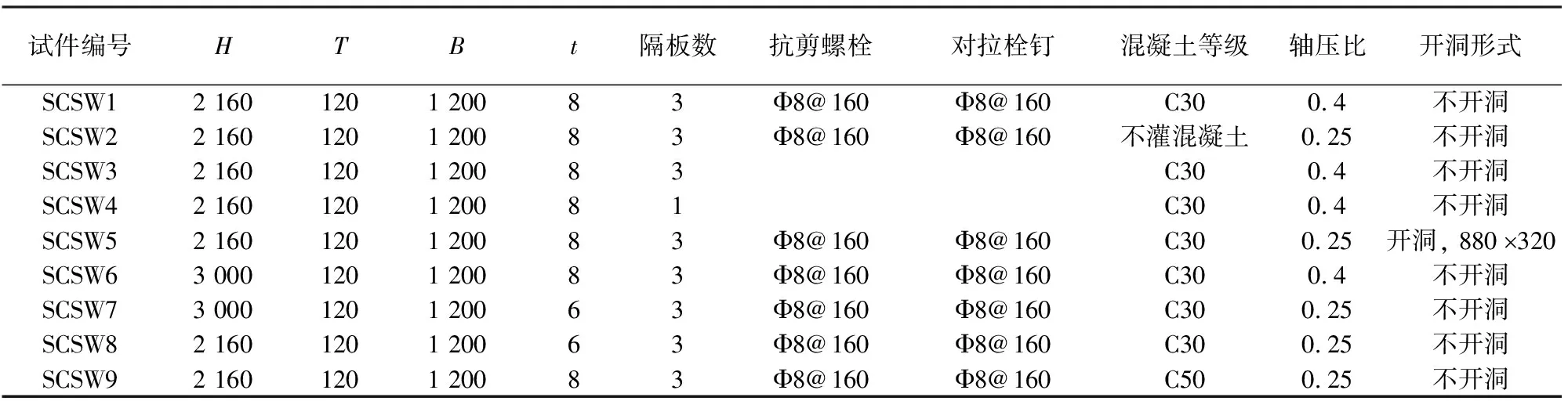
表1 试件设计参数

加载模式设计按要求的轴压比，将竖向荷载一次加载完成，并保持恒定不变，然后根据计算得到的屈服位移δy，在试件屈服前，按0.3δy, 0.7δy, 1.0δy的荷载分级模式在加载梁上进行水平加载；在试件屈服后，以δy为级差加载，直至破坏.屈服前，每级加载循环2圈，屈服后，每级加载循环3圈.

1.2 试验现象

通过试验得到了组合剪力墙的破坏模式.随着荷载增大，翼缘板边缘最先屈服.试件进入塑性后，钢板表面油漆逐渐脱落，当材料强度得到充分发挥时，试件端部钢板开始鼓曲，试件达到极限承载力.与纯钢板剪力墙和没有对拉栓钉剪力墙的破坏模式不同，该类试件的破坏模式为：底部混凝土压碎、对拉螺栓拉断、底部钢板鼓曲，试件失效或破坏.如图2所示.

(a) 加载初期

(c) 破坏阶段

2 剪力墙数值计算模型

2.1 有限元模型

根据剪力墙试验模型，可将有限元模型的约束条件简化为下端固定、上端自由.墙体长度取刚性支座顶面到加载梁水平中心线间的垂直距离，墙体的横截面尺寸为各试件的实测尺寸，由于加载梁刚度比下部试件的刚度大很多，因此，可忽略加载梁的变形，加载梁只起到分担荷载的作用.由试验可知，墙体整体偏心很小，建模时，可忽略墙体的安装偏差，假定竖向力和水平力作用在墙体中心.模型的总体几何初始缺陷模式可根据一阶屈曲模态确定，初始缺陷幅值取H/1 000.

采用Abaqus中的C3D8R实体单元模拟混凝土，S4R壳单元模拟钢板，T3D2梁单元模拟栓钉.划分单元时，高度方向和宽度方向以40 mm为一个单位，厚度方向以30 mm为一个单位.剪力墙有限元模型如图3所示.几何初始缺陷如图4所示.由于隔板和栓钉约束，钢板与混凝土连接良好，钢板到加载后期呈现塑性时才出现屈曲.因此，在有限元模拟时，忽略混凝土与钢板之间的黏结滑移.

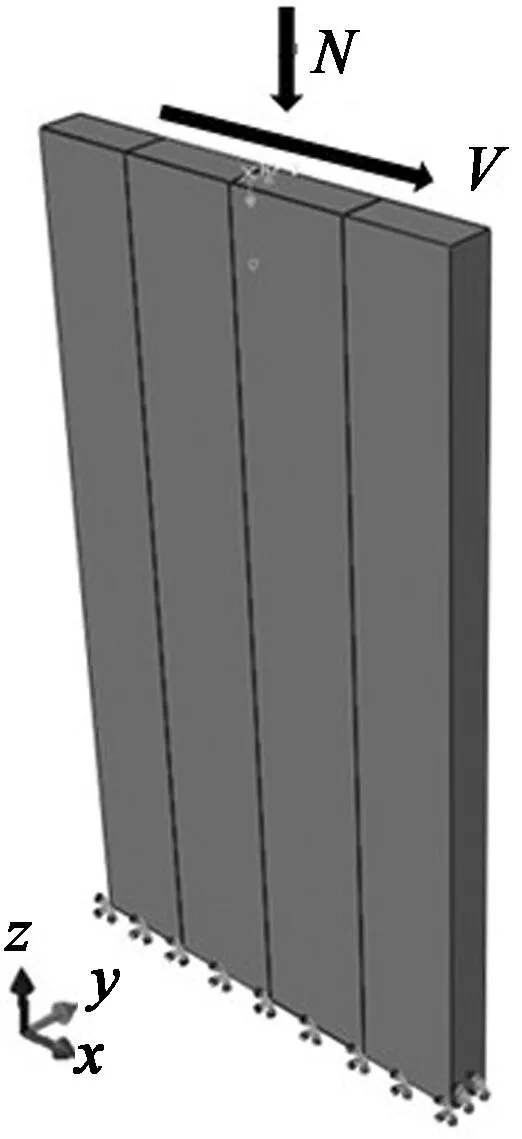
图3 有限元模型

图4 试件几何初始缺陷

2.2 材料本构关系

根据滞回性能特点，选取能够考虑反复受力状态的材料本构关系.钢材采用混合强化本构关系(linear kinematic hardening model)，屈服值、极限值选取材性试验数值.8 mm厚钢板的材性曲线如图5所示.动力强化系数C根据式(1)[11]代入材料极限应变和极限应力确定.

(1)

式中：σlim为极限强度；σ0为屈服强度；εpl为极限塑性应变.

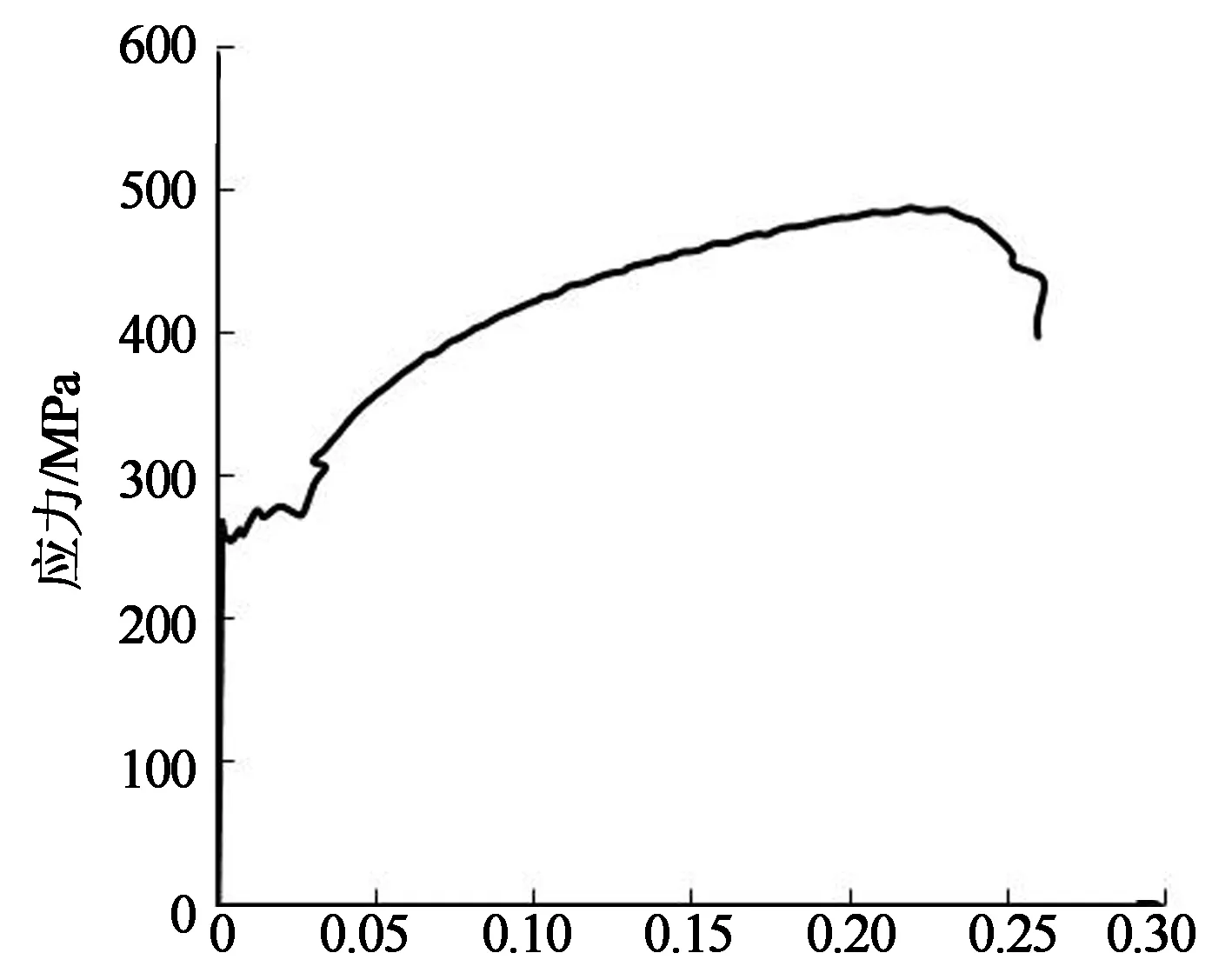
应变/10-6

混凝土材料的本构关系选取能够考虑混凝土损伤的混凝土塑性损伤模型(concrete damaged plasticity model).受压强度曲线采用文献[12]给出的曲线，强度峰值按试验数值确定，其余数值点按照文献[12]的材料本构曲线等比例调幅得到.受拉曲线、混凝土损伤系数均按照文献[12]确定.C30混凝土本构关系曲线如图6所示.

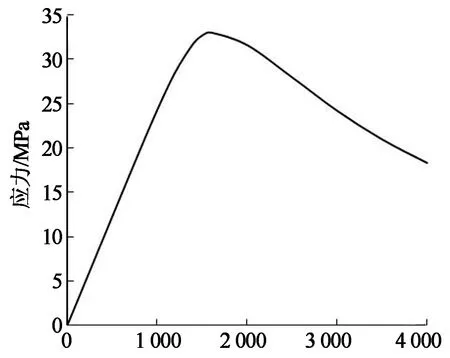
应变/10-6

3 数值计算结果与试验结果比较

3.1 荷载-位移滞回曲线比较

为了对比分析有限元数值计算结果与试验结果的差异，图7给出了部分剪力墙模型在墙顶反复水平力循环荷载作用下数值计算及试验的荷载-位移滞回曲线.图中纵坐标为作用于墙顶的荷载V，横坐标为对应的水平位移δ.

从荷载-位移滞回曲线的比较分析可以看出，本文考虑初始几何缺陷的有限元模型能够准确模拟试件的实际受力状态.但是，在试件进入破坏阶段承载力下降时，由于不能完全考虑混凝土压碎等因素，有限元计算曲线没有明显的下降段，在试件达到承载力以后计算结果不够准确.

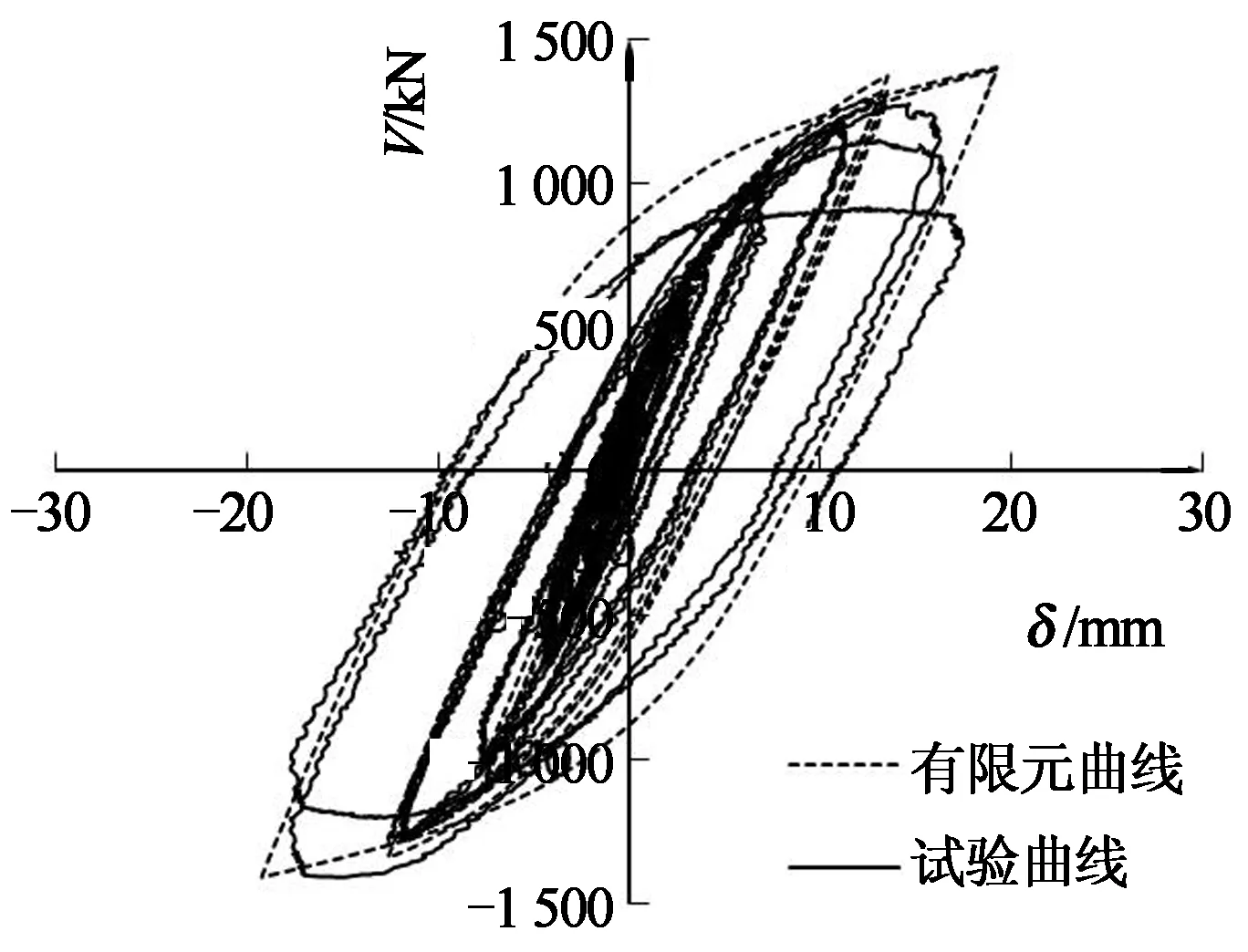
(a) 模型SCSW1

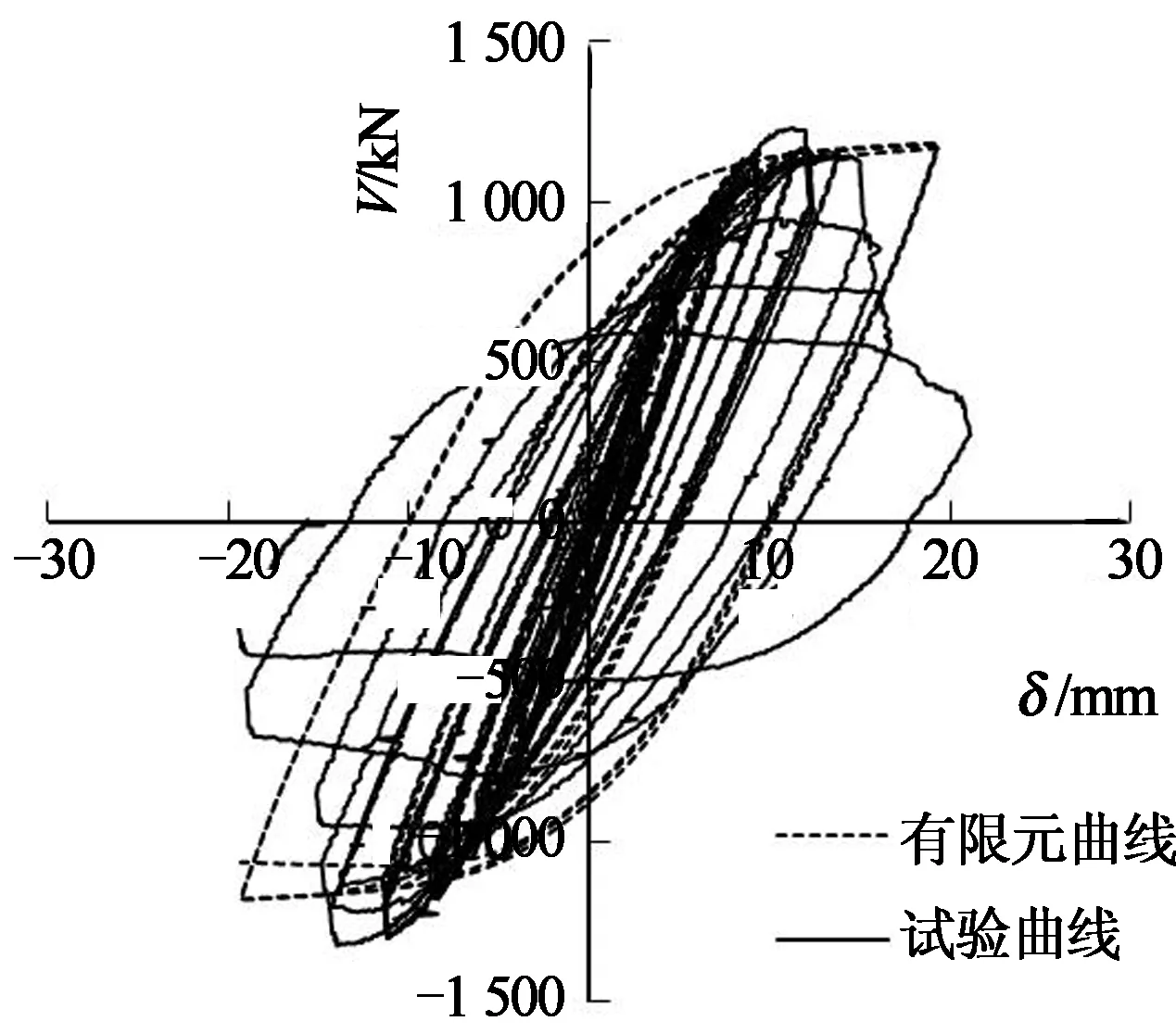
(b) 模型SCSW3

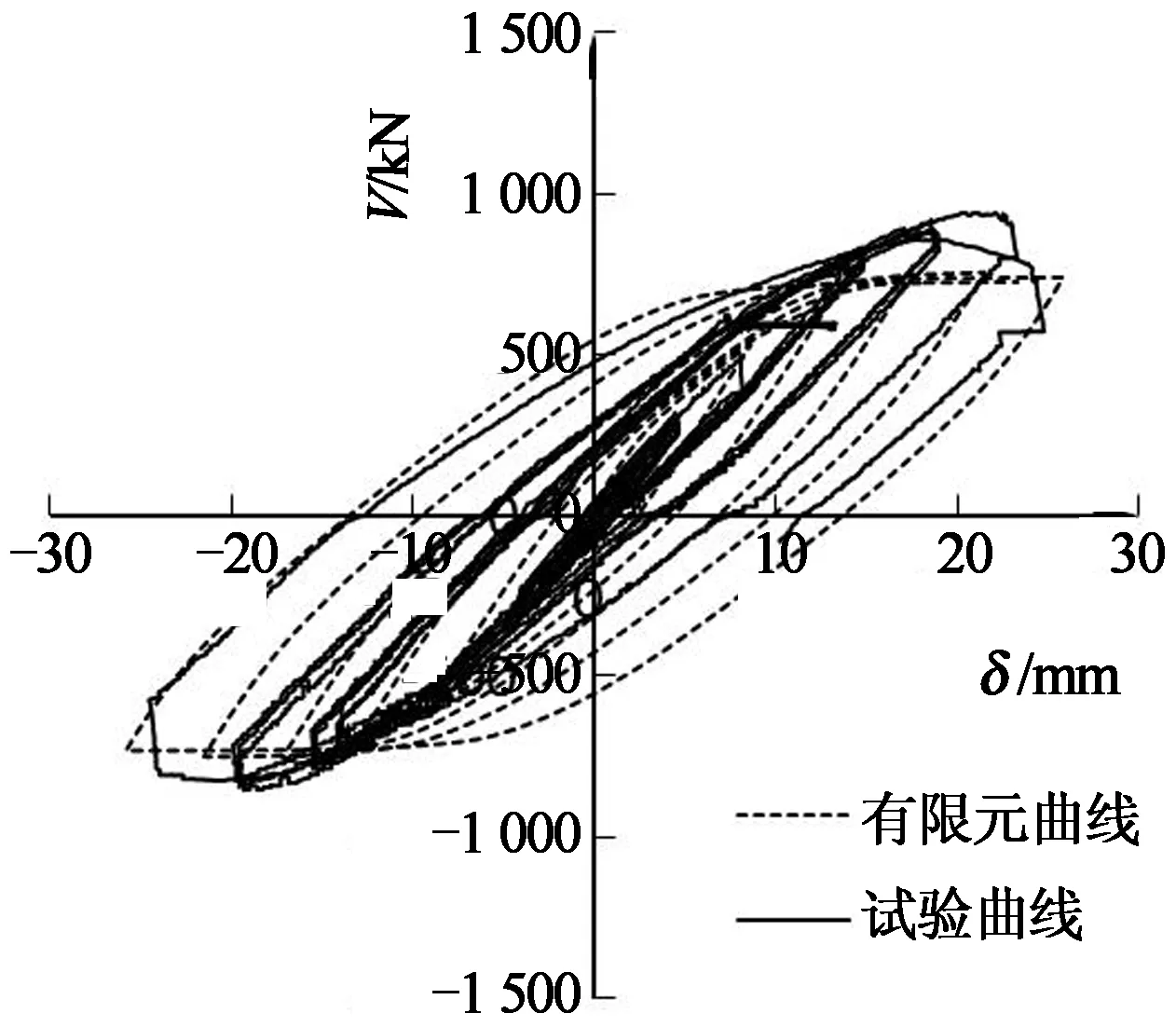
(c) 模型SCSW6

3.2 破坏模式比较

图8为典型试件试验得到的破坏模式，剪力墙底端附近两侧腹板出现鼓曲.图9为相应模型有限元模拟计算得到的破坏模式.可以看出，两者基本相同.不同的是，实际试验加载中，在承载力下降段，由于竖向力的作用，钢板剪力墙腹板出现了两层鼓曲现象.

图8 试件破坏模式

图9 有限元分析得到的试件破坏模式

从试验现象和有限元分析结果可以推断出双层钢板-内填混凝土组合剪力墙的破坏模式.在水平力加载初期，钢板与混凝土均处于弹性状态，两者共同受力、变形协调.当水平力加载到一定数值时，边缘混凝土拉裂，初始刚度下降，随后边缘的钢板屈服，多余的力转移到边缘混凝土上.当达到抗压强度时，混凝土压碎.由于钢板的约束作用，混凝土强度虽然有些下降，但是还能继续承载，这时构件的整体刚度开始下降，边缘的钢板已经进入强化阶段，塑性区也逐步扩大.当水平力继续加载时，边缘的钢板开始鼓曲，这时边缘钢板不能承担原来的荷载，它所承担的一部分荷载由靠近中和轴的部分继续承担.构件的刚度继续下降.当剩余的截面不能抵抗继续增加的荷载时，荷载-位移曲线开始进入下降段，构件达到极限承载状态.从试验现象和有限元分析结果可看出，在小偏心轴力情况下，拉结筋符合一定间距要求时，构件材料屈服总是先于构件局部屈曲出现.

4 参数分析

从上述有限元数值分析与试验结果的比较可看出，两者吻合良好.因此，本节基于以上数值计算模型，以轴压比、墙体高宽比、宽厚比为主要参数，采用Abaqus软件研究低周反复荷载作用下双层钢板内填混凝土组合剪力墙水平荷载-位移(P-Δ) 骨架曲线的变化规律.本文算例的基本参数为：墙宽B=1 200 mm，钢板厚t=8 mm，螺栓间距和隔板间距取值与试验模型相同，轴压比参数变化为0, 0.2, 0.4, 0.6, 0.8，高宽比参数变化为1.2, 1.4, 1.8, 2.2, 2.6，宽厚比参数变化为4, 6, 8, 10, 12.图10～图15为计算得到的各参数对骨架曲线的影响.

由图10和图11可看出，高宽比H/B对承载力和初始刚度均有影响，随着高宽比的增大，承载力逐渐下降，初始刚度也逐渐下降.当高宽比小于1.4时，骨架曲线在到达峰值荷载后略有上升；当高宽比大于1.4时，骨架曲线到达峰值荷载后开始下降.影响曲线近似呈抛物线形状.这说明随着高宽比的增大，试件失稳的可能性也在增加.试件逐渐由剪切破坏变为弯剪破坏.

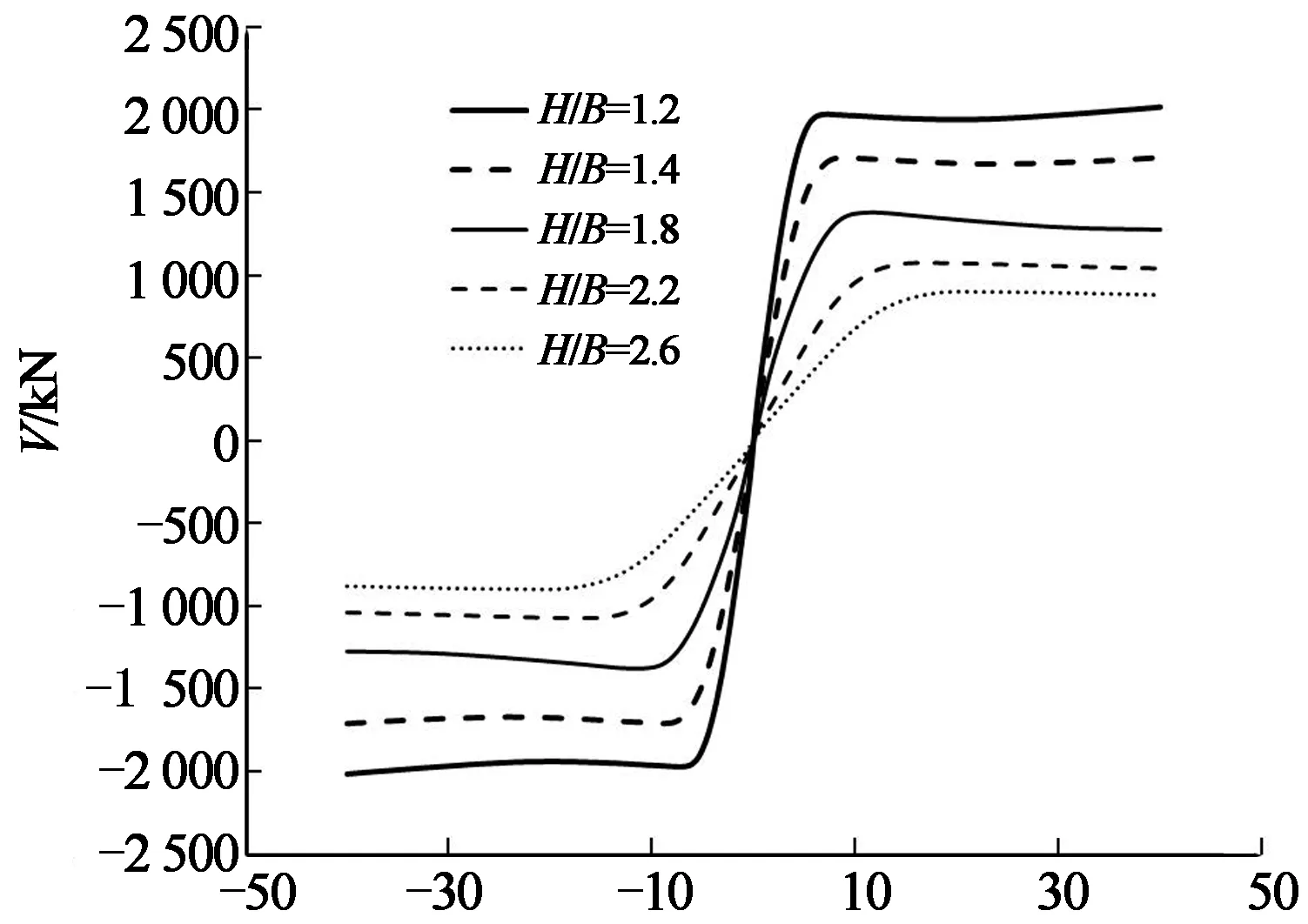
Δ/mm

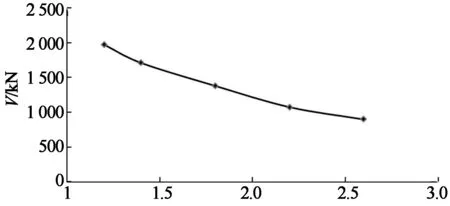
H/B

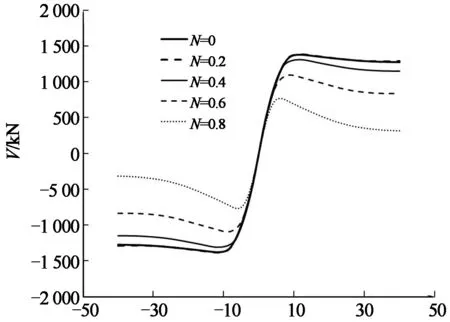
Δ/mm

Δ/mm

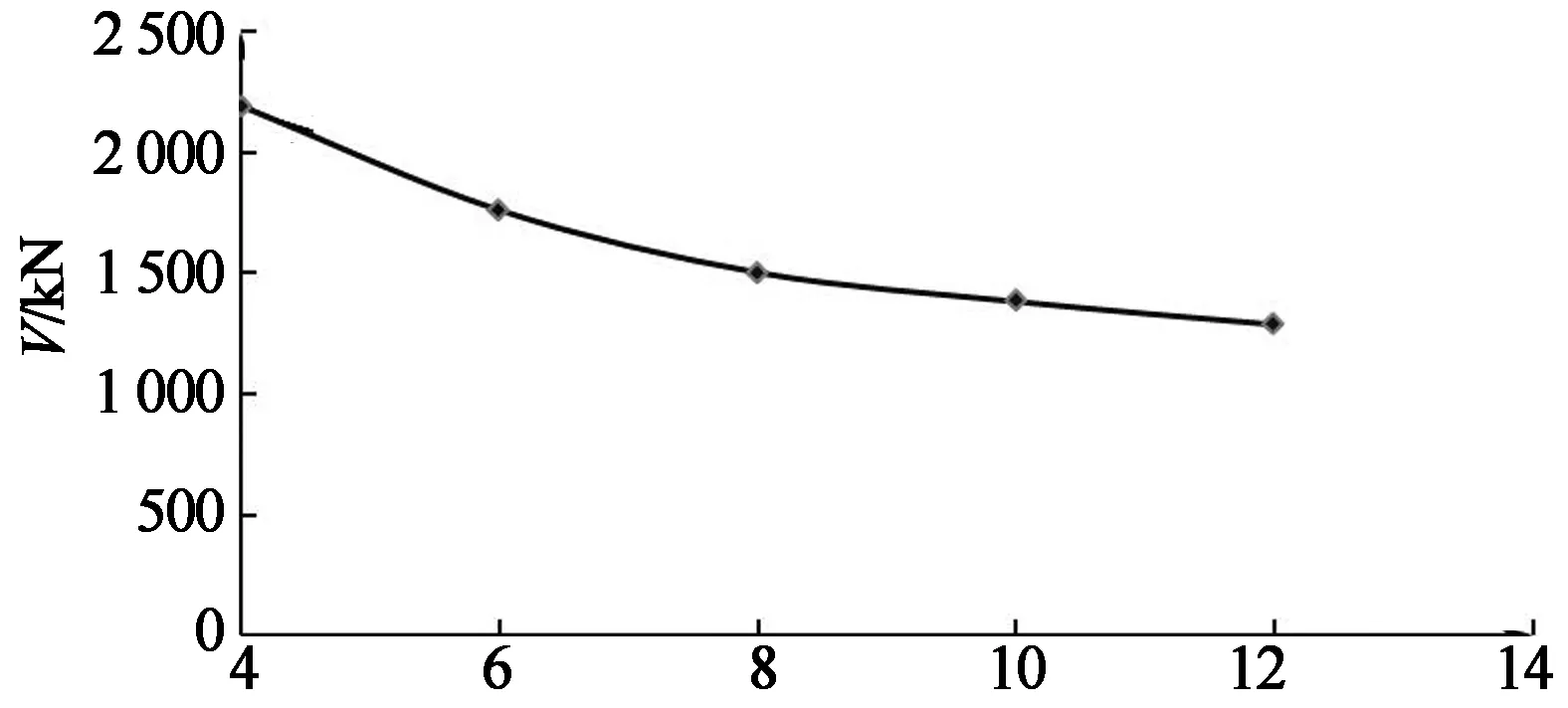
B/T

由图12和图13可看出，轴压比N对构件的初始刚度影响不大，但对曲线的形状和峰值荷载大小有较大影响.当轴压比小于0.2时，随着轴压比增加，构件峰值荷载略有上升，并且下降段下降缓慢；当轴压比大于0.2时，随着轴压比增加，构件峰值荷载降低，并且曲线下降段变得陡峭.这说明轴压使得构件的变形能力变差，特别当轴压比大于0.2时，由于二阶效应的影响，当承载力达到极限承载力后，构件性能迅速下降.

由图14和图15可看出，宽厚比B/T对构件承载力和初始刚度均有影响，但到达峰值时的位移基本相同.随着宽厚比增加，承载力和初始刚度都有所降低.影响曲线近似呈抛物线形状.这说明宽厚比越大，构件在水平力作用下越容易失稳，特别是对于“一”字型的剪力墙影响更加明显.

5 结 论

1) 本文有限元数值计算结果与模型试验结果吻合良好.因此，实际结构数值分析应考虑初始几何缺陷的影响.

2) 剪力墙高宽比、宽厚比、轴压比对其受力性能均有影响.随着试件高宽比和宽厚比的增大，承载力都有下降趋势，影响曲线近似呈抛物线形状.轴压比对其承载力的影响主要表现在0.2以后.当轴压比小于0.2时，随着轴压比的增加，构件的峰值荷载略有增大，并且下降段下降缓慢.当轴压比大于0.2时，随着轴压比的增加，构件峰值荷载降低，并且下降段曲线变得陡峭.

3) 高宽比、宽厚比是影响其初始刚度的主要因素.高宽比越小，初始刚度越大.宽厚比越大，初始刚度越大.轴压比对构件初始刚度的影响很小.

致谢：感谢南通建筑工程总承包有限公司为本研究提供试件.

[1] 廖飞宇，陶忠，韩林海. 钢-混凝土组合剪力墙抗震性能研究简述[J]. 地震工程与工程振动, 2006, 26(5): 129-135.

LIAO Fei-yu, TAO Zhong, HAN Lin-hai. A state-of-the-art review of composite shear walls under cyclic loading[J]. Earthquake Engineering and Engineering Vibration, 2006, 26(5): 129-135. (In Chinese)

[2] HOSSAIN K M A, WRIGHT H D. Behaviour of composite walls under monotonic and cyclic shear loading[J]. Structural Engineering and Mechanics, 2004, 17(1): 69-85.

[3] HOSSAIN K M A, WRIGHT H D. Finite element modelling of the shear behaviour of profiled composite walls incorporating steel-concrete interaction[J]. Structural Engineering and Mechanics, 2005, 21(6): 659-676.

[4] EOM T S, PARK H G, LEE C H,etal. Behavior of double skin composite wall subjected to in-plane cyclic loading[J]. Journal of Structural Engineering, 2009, 135(10): 1239-1249.

[5] 聂建国,陶慕轩,樊建生. 双钢板-混凝土组合剪力墙研究新进展[J]. 建筑结构, 2011(12): 52-60.

NIE Jian-guo, TAO Mu-xuan, FAN Jian-sheng. Research advances of composite shear walls with double steel plates and filled concrete[J]. Building Structure, 2011(12):52-60. (In Chinese)

[6] LINK R A, ELWI A E. Composite concrete-steel plate walls: analysis and behavior[J]. Journal of Structural Engineering, 1995, 121(2): 260-271.

[7] PRYER J W, BOWERMAN H G. The development and use of British steel bi-steel[J]. Journal of Constructional Steel Research, 1998, 46(1): 15.

[8] 司波，白正仙. 双层钢板剪力墙的初始抗侧刚度分析[J]. 长春工程学院学报:自然科学版, 2006, 7(1): 8-11.

SI Bo, BAI Zheng-xian. Analysis of initial stiffness against lateral displacement of double steel plate shear wall[J]. Journal of Changchun Institute of Technology: Natural Science, 2006, 7(1): 8-11. (In Chinese)

[9] 黄会平. 双层钢板内填混凝土组合剪力墙性能研究[D]. 南京：东南大学土木工程学院, 2009.

HUANG Hui-ping. Reseach of performance of double-steel-layer-concrete composite shear wall[D]. Nanjing: College of Civil Engineering, Southeast University, 2009.(In Chinese)

[10]祝文君. 内填混凝土双层钢板组合剪力墙抗震性能研究[D]. 南京：东南大学土木工程学院, 2010.

ZHU Wen-jun. Research on the seismic behavior of bi-steel-plate composite shear wall with concrete-plate filled[D]. Nanjing: College of Civil Engineering, Southeast University, 2010. (In Chinese)

[11]HIBBITT K. ABAQUS theory manual and analysis user′ s manual[R]. Pawtucket, USA: Sorensen, Inc, 2002.

[12]GB 50010—2010 混凝土结构设计规范[S]. 北京：中国建筑工业出版社，2011：207-220.

GB 50010—2010 Code for design of concrete structures[S]. Beijing: China Building & Architecture Press, 2011：207-220. (In Chinese)