分簇型无线传感器网络时间同步机制的研究

杨 东，李灯熬，赵菊敏，安文秀

(太原理工大学信息工程学院，山西太原 030024)

无线传感器网络(WSN)是近年来逐渐兴起的一种融多种技术的新兴领域，用以自动感知、采集、传输和实时监测待检测对象信息［1］。无线传感器网络是一种面向应用的网络，在实际应用中，缺乏时间信息的监测结果对于监测者来说是不具有任何意义的。时间同步机制的性能对无线传感器网络有着至关重要的影响。

WSN时间同步机制于2002年由Elson［2］等人在Hot-Net－Ⅰ国际会议上首次提出，并被无线传感器网络研究者广泛关注。多年来众多研究学者已提出了多种经典时间同步算法。现行的经典时间同步算法可分为3类:基于接收者—接收者的时间同步算法(典型代表算法RBS［3］)、基于接收者—发送者的时间同步算法(典型代表算法TPSN［4－5］)和基于发送者的时间同步算法(典型代表算法DMTS［6］和 FTSP)。

随着无线传感器网络研究水平提高及应用的推广，网络的大规模性成为无线传感器网络发展的必然趋势。时间同步机制的研究也必然致力于在降低网络能量消耗的基础上提高大规模网络的时间同步精度。在网络规模增大和网络消耗降低的要求下，已有的很多算法得到了限制［7］。RBS 算法复杂度为O(m，n)，信息交换量为O(n2)(m，n分别为广播消息的个数和节点数目)。当节点数目较大时，信息交换量非常大，消耗网络较多的能量，不适用于节点数目较多的网络。同时RBS算法只能相对同步，同步精度较低。DMTS同步算法是以在牺牲同步精度的基础上，降低算法的复杂度和网络的开销，只能适用于对同步要求不是很高的网络，不能适应未来无线传感器网络的发展要求。FTSP算法中，参考节点多次发送广播消息，通过集中式线性回归法对时钟的相对漂移和相对偏移进行估计。当网络中节点数目较多时，FTSP算法需要非常多的能量来维护大量的历史数据，用来提高估计精度，从而加大了网络的能量消耗。

TPSN算法应用于层次型网络结构，采用双向同步机制，同步精度较高，在同步过程中信息交换量为O(2n+1)。当n变大时，TPSN算法的信息交换量远低于RBS的信息交换量，常用于大规模网络，且易于实现。但是TPSN算法中未考虑根节点的失效问题，且同步精度随着网络跳数的增加而降低。考虑到上述问题，本文提出了一种新的同步算法:创建分簇型网络结构，通过分簇降低网络跳数避免同步误差的积累量增大，同时用簇首节点代替根节点，通过周期性选取簇首节点，均衡簇首节点的能量消耗，降低簇首节点的失效率。在同步过程中，同时采用单向广播同步机制和双向时间同步机制，提高同步过程中的同步精度。

1 基于分簇型网络结构的时间同步算法

本文提出的算法分为2个阶段:分簇结构的建立阶段和时间同步阶段。在分簇结构的建立阶段，利用本文提出的优化LEACH算法创建网络拓扑结构，并选取各簇簇首节点，其他节点根据收到簇首节点发送消息的信号强度选择加入簇，使每个节点均处于簇结构中。在时间同步阶段，首先进行的是簇首节点或助理簇首节点与基站之间的时间同步，该阶段使用双向时间同步机制;其次，完成上述时间同步阶段后，开始启动簇首节点与同簇内其他节点的时间同步阶段，在该阶段使用双向时间同步机制与单向广播时间同步机制相结合的时间同步机制。

1.1 分簇型网络结构的创建

在无线传感器网络层次型拓扑控制算法方面，研究者提出了较多经典拓扑结构控制算法。其中，较为经典的是LEACH(Low Energy Adaptive Clustering Hierarchy)算法［8］，该算法能够周期性自动形成簇型网络拓扑结构，运行阶段可分为簇的建立阶段和稳定的数据通信阶段。在LEACH算法选取簇首节点过程中，节点产生一个0～1的随机数，若该随机数小于阈值T(n)，则该节点以T(n)的概率当选簇首节点。已当选过的节点则把T(n)的值设置为0，在下轮选取中不再当选。阈值T(n)表示为

LEACH算法可以保证每一个传感器节点以相同的概率当选簇首节点，均衡了簇首节点所消耗的能量，从而避免了因簇首节点能量过低而导致全网络失效的情况出现，较好地提高了整个网络的运行时间。但是LEACH算法存在着一些缺陷:首先，该算法在簇首选取机制中，传感器节点随机数产生的随机性较强，有可能导致产生较多的传感器节点距离簇首节点的位置较远，容易造成簇首节点的能量消耗过多、过快;其次，该算法簇首选取机制中并没有考虑到传感器节点的初始能量和剩余能量的问题，有可能会出现剩余能量较低的节点被选取为簇首节点，加速簇首节点因能量消耗过快而迅速导致死亡。

针对以上LEACH算法中存在的缺陷，本文提出的时间同步算法提供了良好的网络拓扑结构。本文提出了一种LEACH优化算法，在优化算法中，簇首节点选取阈值中融入簇首节点剩余能量和邻居节点密度因子，同时在非簇首节点中选取助理簇首节点用以均衡簇首节点的能量消耗。设定簇首节点选取的时间门限值Tth，该值与节点的剩余能量相关，使簇首节点的当选周期与剩余能量有关。优化算法的具体描述如下:

定义E0为传感器节点的初始能量，在本文中，假定所有传感器节点的初始能量E0是相等的;定义Eres(r)为第r轮簇首节点选取时，节点i的剩余能量，则节点i从网络结构初始化至第r轮簇首选取时，因接收、发送消息共消耗的能量(r)，(r)分别为

式中:为第m轮期间，节点i接收数据的比特数;为第m轮期间，节点i发送数据的比特数;dm为第m轮期间节点i的通信距离总和。

在综合分析以上两个因素对簇首节点的影响后，结合上述公式，本文提出了优化算法的簇首节点选取机制的阈值T'(n)，T'(n)表达式为

式中:N为无线传感器网络簇首节点的总次数;α根据网络的实际情况确定且0＜α＜1。

由于簇首节点在整个时间同步算法中具有重要的作用，其一但失效不仅会影响时间同步机制的同步精度，严重者甚至会危及整个无线传感器网络的使用寿命。同时，簇首节点将与基站和簇内非同步节点进行大量的信息交换，能量消耗要远超过簇内其他节点。为了均衡簇首节点的能量消耗，提高整个网络的能量利用率，本文提出一种簇首节点助理机制。在该机制中，该节点主要用来实现数据融合并将融合后的数据传递给基站。所以在助理簇首节点选取的过程中，该节点与基站位置的距离成为重要的选取原则。定义dBS(i)为节点i与基站之间的距离，则助理簇首节点的选取阈值为

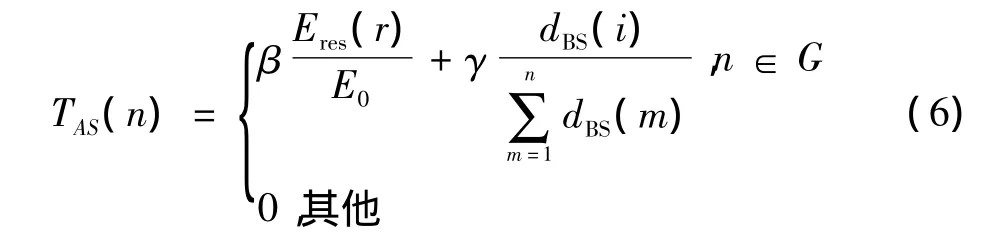
式中:β和γ均根据网络的实际情况所定，β和γ均为小于1的实数;G'为簇内非簇首节点。

1.2 时间同步阶段

时间同步阶段主要分为2个阶段:簇首节点及助理簇首节点与基站的时间同步阶段;簇首节点与同簇内待同步节点时间同步阶段。在簇首节点及助理簇首节点与基站间的时间同步阶段采用双向时间同步机制。在簇首节点与同簇内的其他待同步节点时间同步阶段采用双向时间同步机制和单向时间同步机制混合式时间同步机制。

在簇首节点及助理簇首节点与基站实现时间同步的阶段，时间同步原理如图1所示，簇首节点或助理簇首节点在T1时刻向基站发送时间同步请求消息，基站在T2时刻收到该请求消息后，并在T3时刻响应该消息，簇首节点或助理簇首节点在T4时刻收到基站发送的响应消息。根据式(7)和式(8)计算自身节点与基站之间的时间偏差和时间消息传播时延，并根据计算结果调整自身本地时钟，从而实现簇首节点或助理簇首节点与基站的时间同步。

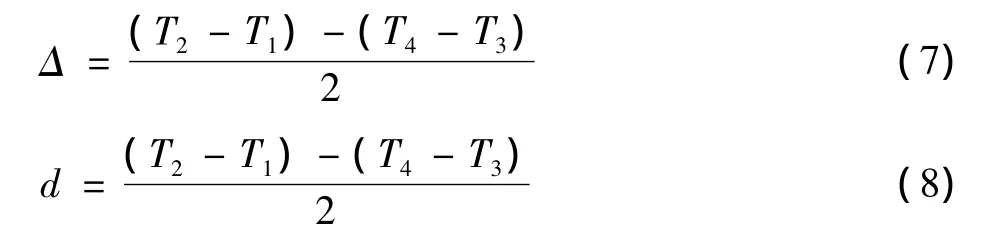
式中:d为消息传播时延;Δ为两节点间的时间偏移值。

图1 簇首节点或助理簇首节点与基站时间同步原理图

在簇首节点与同簇内待同步节点时间同步阶段，采用双向时间同步机制和单向广播时间同步机制混合式时间同步机制。具体同步过程如下:

1)簇首节点在T1时刻广播启动簇内节点时间同步消息，簇内各节点记录各自收到该广播消息的时刻Tk(i)，并保存该时刻。

2)随机选择一簇内待同步节点，并在T2时刻响应该广播消息，并发送响应消息给簇首节点。该消息中包含其在步骤1)中收到的时间同步启动消息的时刻T2和发送响应消息的时刻T3。

3)簇首节点于T4时刻收到该响应节点发送的响应消息，并根据式(7)和式(8)计算簇首节点与该相应节点间的时间偏移值Δ和消息传播延迟d。

4)簇首节点广播时间校正消息，该消息中包含响应节点在步骤1)中收到的时间同步启动消息的时刻T2以及步骤3)中簇首节点计算出的时间偏移值Δ和消息传播延迟d。

5)簇内待同步节点收到步骤4)中的时间校正消息后，读取该消息包，比较在步骤1)中自身保存的Tk(i)与T2值的大小，得到自己与簇首节点间的时钟偏差，并根据δ'调整本地时钟，从而实现待同步节点与簇首节点间的同步。

簇首节点与同簇内待同步节点时间同步机制原理图如图2所示。

2 实验仿真分析

图2 簇首节点与同簇内待同步节点时间同步原理图

为了验证本文提出的优化算法性能，对所提出的优化算法进行了实验仿真，并与TPSN算法的实验仿真结果进行比较。在实验中假设基站的能量是无穷的，所有传感器节点均是不可移动的。其中，节点部署范围100 m×100 m，基站位置(50，50)，节点数300，节点的初始能量E0为0.15 J，Eelse为50 nJ/bit，Efs为10 pJ/(bit×m2)。

从图3可知，本文算法与TPSN算法随着节点数目的增加，节点的信息交换量也随之增加。当网络节点数目小于50时，二者之间的差距不明显，但是随着网络中节点数目的增多，TPSN算法中的信息交换量要明显大于相同数目下本文算法中的信息交换量。导致这种情况出现的原因是:TPSN算法中同步节点采用双向时间同步机制，每对节点间实现同步需要2条消息进行交换。而在本文算法中，只有簇首节点和助理簇首节点采用双向同步机制，而在簇内节点进行同步时，采用单向广播时间同步机制。在整个网络中，采用单向广播时间同步机制的节点数目要远小于采用双向时间同步机制的节点数目。所以当网络中节点数目增多时，本文算法在信息交换量的优势明显优于TPSN算法。

图3 本文算法与TPSN算法信息交换量的比较

由图4可知，本文算法与TPSN算法在同步过程中，随着跳数的增加同步误差越来越大。TPSN中同步误差一方面由于双向时间同步机制中存在消息传播时延，更主要的是随着跳数的增加，同步误差在逐渐积累，导致随着跳数的增加同步误差越来越大。本文算法中出现的同步误差首先出现在簇首节点与基站进行的双向时间同步机制，其次，较大程度的同步误差是由于簇首节点在簇内节点同步过程中随机选择的应答节点。若应答节点与周围邻居节点的时钟偏移存在较大误差，则也会导致本文中同步精度的降低。同时，亦可观察到，当网络跳数等于1时，二者之间存在较小的差距，但是随着跳数的增加，在相同的网络跳数情况下，本文的同步误差要小于TPSN算法中的同步误差，即本文的时间同步精度要高于TPSN时间同步精度。

图4 本文算法与TPSN算法同步误差的比较

如图5所示，在相同的轮数情况下，本文算法节点消耗的能量要低于TPSN算法。其主要原因是在本文算法中采用分簇型网络结构，在簇首节点阈值中融入节点剩余能量因子和邻居节点密度因子。邻居节点密度因子越大，簇首节点周围的邻居节点数目也就越多，簇内节点的部署也越均匀，簇首节点的通信总距离也就越小，从而簇首节点的通信消耗也就越小。另一方面，本文设定簇首节点的当选时间门限值，该值随着簇首节点剩余能量的变化自动变化簇首时间的当选周期，剩余能量越低，簇首节点的当选时间也就越短，缩短簇首节点的工作时间，从而降低了节点的能量消耗。最后，本文中助理簇首节点均衡了簇首节点的能量消耗，提高了网络利用率。

3 总结

本文提出一种新的时间同步算法，在该算法的分簇结构创建阶段，簇首选取阈值融入簇首节点的剩余能量因子和邻居节点密度因子，同时设定了助理簇首节点和簇首节点工作时间门限值，较好地优化了网络结构，降低了网络的跳数。在时间同步阶段，采用了双向时间同步机制和单向广播时间同步机制。实验证明，该算法降低了网络跳数，提高了时间同步精度，降低了节点的能量消耗，延长了无线传感器网络的运行寿命，具有一定的实用价值。

图5 本文算法簇首节点与TPSN算法根节点剩余能量比较

:

［1］程敏敏，宋家友，张汉.基于梯度的分簇式路由协议［J］.电视技术，2012，36(15):108－111.

［2］汪富强，曾鹏，于海斌.一种低开销的时间同步算法［J］.仪器仪表学报，2011，32(6):1357－1361.

［3］ELSON J，GRIOD L，ESREIN D.Fine－grained network time synchronization using reference broadcasts［C］//Proc.5th Symposium Operating Systems Design and Implementation.Boston，MA:ACM Press，2002:147－163.

［4］GANERIWAL S，KUMAR R，SRIVASTAVA M B.Timing－sync protocol for sensor networks［C］//Proc.1st International Conference on Embedded Networked Sensor Systems(SenSys 2003).Los Angeles，CA:IEEE Press，2003:138－149.

［5］GANERIWAL S，KUMAR R，ADLAKHA S，et al.Network－wide time synchronization in sensor networks［EB/OL］.［2013－02－10］.http://nesl.ee.ucla.edu/fw/ram/ram － homepage/content/papers/time_sync.pdf.

［6］PING S.Delay measurement time synchronization for wireless networks［EB/OL］.［2013－02－10］.http://www.intel_research .net/publication/Berkeley/0811200031327－137.pdf.

［7］孙利民，李建中，陈渝，等.无线传感器网络［M］.北京:清华大学出版社，2005.

［8］周治平，王亭，张明亮.传感网络中一种能量有效的簇头选举机制［J］.计算机工程与应用，2012，48(8):105－108.