一种基于CS的LDPC码的抗误码方法

马文萱，谢正光，张 辉，徐 伟

(南通大学电子信息学院，江苏南通 226019)

随着多媒体技术的迅猛发展，视频应用的范围越来越广泛。庞大的数字化视频数据需要进行高效压缩，压缩后的码流对信道误码十分敏感。现有的视频编码标准(H.264/AVC)［1］大多以预测编码为基础，一旦某帧在传输过程中发生错误，就会导致其后续帧的错误累积。

传统抗误码方法可分为3种［2］。一种是在编码端使用冗余容错的方法，如冗余片、灵活宏块调整、帧内刷新、可伸缩性编码［3］以及多重描述编码［4］，然而这些方法增加了冗余数据，使得信道的利用率下降。另一种是在解码端使用错误隐藏、数据恢复［5－6］的方法，但这些方法只是尽可能地弥补误码所带来的图像视觉损伤，并不能真正地抑制差错飘移。第3种在视频传输的过程中使用某种纠错方法:比如前向纠错，该方法的不足之处是当错误率超出了信道编码预设的纠错能力时，所重建的视频质量就会迅速下降，呈现所谓的“悬崖效应”。上述表明传统抗误码方法存在诸多不足。

压缩感知理论［7］可以从很少采样数据中高准确率重构出原来信号的特性，受到了人们的重视。本文对压缩感知线性规划解码和信道码线性规划解码进行了研究，利用它们之间的联系，提出了一种基于压缩感知的LDPC码的抗误方法。相对于传统误码，它在高误码率时表现出良好的性能。

1 压缩感知线性规划解码

1.1 压缩感知

压缩感知理论首先由 Candes、Romberg［8］、Tao［9］和Donoho［10］等人在2004年提出文献直到2006年才发表。Candes证明了只要信号在某一个正交空间具有稀疏性，就能以较低的频率(M≪N)采样信号，而且能以高概率重构该信号。压缩感知理论指出，设长度为N的信号X在某组正交基或紧框架ψ上的变换系数是稀疏的，如果用一个与变换基ψ不相关的观测基φM×N(M≪N)对系数向量进行线性变换，并得到观测集合M×1。那么就可以利用优化求解方法从观测集合中精确或低概率地重构原始信号X。压缩感知理论是一种新的在采样的同时实现压缩目的的理论框架，其框架如图1所示。

图1 压缩感知理论框架

首先，如果信号X∈Rn在某个正交基或紧框架ψ上是可压缩的，求出变换系数Θ=ΨTX，Θ是Ψ的等价或逼近的稀疏表示;第二步，设计一个平稳，与变换基Ψ不相关的M×N维观测矩阵Ψ，对Θ进行观测得到观测集合Y=ΦΘ=ΦΨTX，该过程也可以表示为信号X通过矩阵ACS进行非自适应观测:Y=ACSX(其中ACS=ΦΨT)，ACS称为CS信息算子［11］;最后，利用0－范数意义下的优化问题求解X的精确或近似逼近，见式(1)，稀疏信号e，对于合适的HCS，CS－OPT产生的估计值等于e，见式(2)。

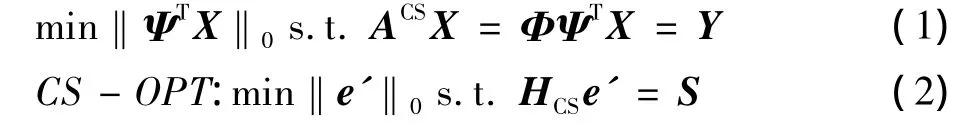
假设输入信号为x，输出信号为y，并且这个信息符号在块长度为n、维度为k=n－rank(Hcs)的实值码CCS的帮助下编码，过程如下:

1)CCS码满足 CCS∈{x∈Rn∣ HCS·x=0}。

2)假设一个生成矩阵GCS∈Rn×k满足CCS∈{GCS·u∣u∈Rk}，通过这个生成矩阵进行x=GCS·u运算，信息向量u∈Rk被编码成码字x∈Rn。

3)设y∈ynCS为接收到的向量。对于一个合适的定义向量e∈Rn，称作错误向量，可以写成y=x+e。假设这个e是稀疏的，也就是说非零项个数被一些正整数k限制。

4)首先接收端计算

式中:

然后通过解决CS－OPT来获得对e的估计，通过=y－求得，又因为是线性码即可得到。求解CSOPT问题的计算极不稳定而且是NP难问题［12］。Chen，Donoho和Saunders［11］指出求解一个更加简单的L1优化问题会产生同等的解，即

1.2 CS－LPD与CS－OPT等同的条件

探究CS－LPD与CS－OPT结果等同的条件，就是探究在何种条件下CS－LPD可以准确求解出原来的信号，也就是探究何种测量矩阵的LP松弛是紧的。文献［12］已经指出一个测量矩阵的行数m满足m=Θ(klog(n/k))，则可以通过CS－LPD恢复出k稀疏信号，表示为k=Θ(n)，但是它最适宜的量度要求构造的矩阵的测量值数量线性于信号的维度n。一个证明测量矩阵是“好的”的充分条件是文献［13－14］指出的有限等距性质(Restricted Isometry Property，RIP)，如果测量矩阵满足RIP，则它的LP松弛对于K稀疏向量e是紧的，并且重构可以达到近似稀疏［13］。众所周知，RIP不是一个“好的”测量矩阵的LP松弛的完整特性，而零空间性质［15－16］是一个对于“好的”测量矩阵的必须且充分的条件。

定义1:假设，C∈R≥0。如果C·‖vs‖1≤‖v‖1对于所有v∈nullspaceR(HCS)成立就说明HCS具有零空间性质NSPR≤(S，C)，写成HCS∈NSPR≤(S，C)。如果C·‖vs‖1＜‖v‖1对于所有v∈nullspaceR(HCS)［17］成立就可以说明HCS具有严格的零空间性质NSPR＜(S，C)，写成 HCS∈NSPR＜(S，C)。

定义2:假设k∈Z≥0，C∈R≥0。如果 HCS∈NSPR≤(S，C)对于所有S⊆I(HCS)成立并且S≤k，则认为HCS具有零空间性质NSPR≤(k，C)写成HCS∈NSPR≤(k，C)。如果HCS∈NSPR＜(S，C)对于所有S⊆I(HCS)并且S≤k，则认为HCS具有严格的零空间性质NSPR≤ (k，C)，写成 HCS∈NSPR＜(k，C)。

文献［16］分别给出了如上定义。定义2中的零空间条件对于K稀疏信号的“好的”测量矩阵是必须并且充分的，也就是说对于这些矩阵CS－LPD的估计值等同于CS－OPT的估计值。“好的”测量矩阵的零空间性质是将CS－LPD和CC－LPD联系起来的重要关键点之一。可以得出以下理论:设HCS是一个测量矩阵，并且假设s=HCS·e，而且 e最多有k个非零元素，可以表示为‖e‖0≤k。如果HCS∈NSPR＜(k，C=1)，则由CSLPD产生的估计值e等同于CS－OPT产生的估计值e。

2 信道码线性规划解码(CC－LPD)

2.1 信道码线性规划解码框架

设输入 xCC≜ {0，1}，输出 yCC，信道规则为PY︱X(y︱x)。这个编码方案是以一个块长度为n、维度为k的二元线性码CCC为基础的，n≥k。下面来定义XCC:

1)设 GCC∈为对于CCC的生成矩阵。因此，GCC秩为k，并且信息向量u∈通过x=GCC·u(mod 2)被编码成x∈，也就是CCC={GCC·u︱u∈}。

2)设 HCC∈是一个对于CCC的校验矩阵。因此，HCC的秩n－k≤m，并且对于任x∈，当且仅当x∈CCC时满足HCC·x=0(mod 2)，也就是说CCC={x∈︱HCC·x=0(mod 2)}。3)y∈ ynCC为接收到的向量，定义每个i∈I(HCC)(I(HCC)代表H的行集合)，对数似然比为

4)令yCC是二元的，可以写成y=x+e(mod 2)，e∈为错误向量，s=H·y(mod 2)，s=H·y=H·

CCCCCC(x+e)=HCC·x+HCC·e=HCC·e(mod 2)。最大似然解码(MLD)规则为

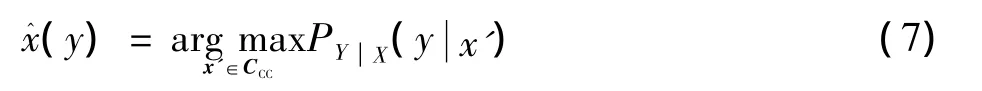
式中:

表示形式如式(4)，即

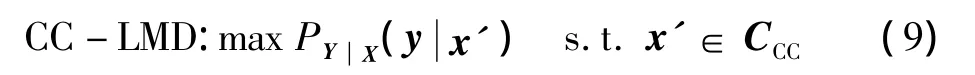
因为代价函数是线性的，并且一个线性函数达到它的凸集的最小极值点，本质上等于CC－MLD2如式(6):

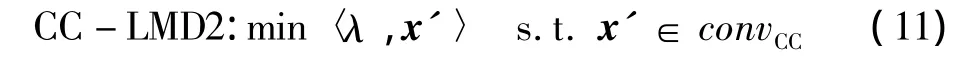
虽然只是一个线性规划问题，但是因为它的描述复杂性高，所以通常不可以有效解决。

C 可以被写成 CCC=CCC，1∩ … ∩ CCC，m，所以conv(CCC)=conv(CCC，1∩ … ∩ CCC，m)⊆conv(CCC，1)∩ … ∩conv(CCC，m)=P(HCC)。在文献［18－19］中如下结论被证实:松弛具有一个重要的性质即所有conv(CCC)的顶点都是P(HCC)的顶点。所以CC－MLD问题转换为CC－LPD问题表示为式(7)，即

2.2 CC－LPD与CC－MLD等同的条件

在二元对称信道中，设HCC为码CCC的一个校验矩阵，设S⊆I(HCC)。如果HCC满足‖ωS‖1＜‖ω‖1，对于所有ω∈k(HCC){0}，则CC－LPD的结果等于这个发送的结果。其中，

3 CC－LPD与CS－LPD之间的联系

由以上分析可知，要知道CC－LPD和CS－LPD之间的联系，就需要理解在零空间里的哪些点可以与在基本多面体空间里的点产生联系。文献［20］中指出如下定理:设HCS是一个0－1测量矩阵，则v∈Nullsp(HCS)⇒|v|∈K(HCS)。即表示在HCS的R零空间的每个点可以联系到HCS的基本锥空间上的一个点。因此，一个对于R零空间的问题点，将会转化成在多面锥上的一个问题点，导致CC－LPD具有糟糕的性能。简单来说，如果一个校验矩阵HCS在多面锥空间里有不低的伪码重量点，则在HCS的R零空间域中没有问题点。在文献［19］中给出了不同信道下的最低伪码重量。

4 实验仿真

4.1 实验步骤

由以上的结论可知，如果一个校验矩阵可以纠正CC－LPD中的k个比特翻转错误，则这个校验矩阵可以作为CS－LPD中的测量矩阵来恢复k稀疏的错误信号。因此可以采用IEEE802.16e标准中的校验矩阵作为解码端压缩感知重构的测量矩阵，实验步骤图见图2。

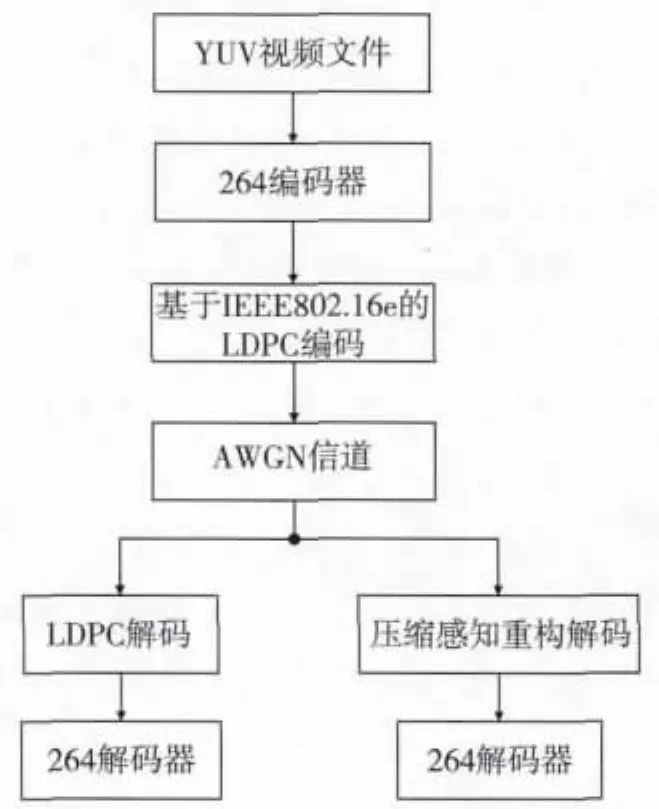
图2 实验步骤图

步骤如下:

1)对YUV文件进行编码:通过264编码器编码为标准视频文件264文件，对264文件的每个NAL的长度进行限制。

2)对264文件进行处理:将264文件按NAL为单位分别存储，转换为二进制数据。IEEE802.16e标准中的码长从 576～2 304不等，码率有 1/2，2/3A，2/3B，3/4A，3/4B，5/6共6种。此次仿真中选取码长为2 304、码率为3/4A进行仿真。对不足2 304长度的NAL进行补0处理。

3)编码:对每一个NAL数据进行基于IEEE802.16e的LDPC编码。

4)信道仿真:分别加入信噪比为－1～+1.8 dB(步长0.2 dB)与1.9～3.5 dB(步长0.1 dB)的噪声。

5)LDPC解码:运用LLR－BP算法进行解码。

6)CS重构解码:设IEEE 802.16e中的校验矩阵为H，经过LDPC编码和信道仿真的信号为y∈F2，其中y=x+e。x∈F2为经过LDPC编码得到的信号，e∈F2为错误信号。将式子两边同时乘以H得到

因为H为x的生成矩阵，且x为线性码，所以H·x(mod 2)为0，所以

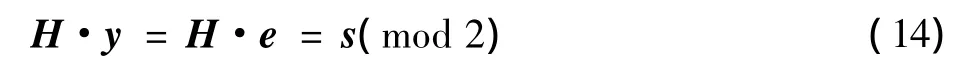
通过求解式(15)得到e，通过回代即可得到y。

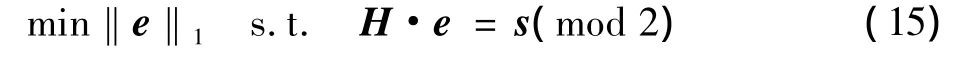
4.2 实验结果

在对 clip_cif.yuv，akiyo_cif.yuv，news_cif.yuv 进行 2种编解码方法得到的264文件解码，发现2种方法能够正确解码的最大误码相差不大，但是解码正确率有很大差异。图3、图4、图5为3个不同文件的解码正确率实验结果图。

图4 两种方法的解码成功率对比图

由图可以看出当信噪比大于2 dB时两种解码方法都可以正确解码，验证了“如果一个校验矩阵可以纠正CCLPD中的k个比特翻转错误，则这个校验矩阵可以作为CS－LPD中的测量矩阵来恢复k稀疏的错误信号”的结论。并且由图可以看出使用CS解码正确率明显高于传统LDPC解码方法。

图5 两种方法的解码成功率对比图

5 结束语

本文利用CC－LPD和CS－LPD之间的联系将压缩感知的重构方法运用在LDPC解码上。实验结果表明本文所提出的基于CS的LDPC抗误方法的解码正确率明显高于传统LDPC解码方法，提高了抗误效果，提高了数据重构的精确性，为后续研究提供了保证，为视频抗误码传输提供了新的思路。

:

［1］王嵩.H.264视频编码新标准及其性能分析［J］.电视技术，2003，27(6):25－27.

［2］WANG Y，STEPBUN W，WEN J T，et al.Error resilient video coding techniques［J］.Signal Processing Magazine，2000，17(4):61－82.

［3］WANG Guijin，ZHANG Qian.Channel－adaptive error protection for scalable video over channels with bit errors and packet erasures［C］//Proc.IEEE International Symposium on Circuits and Systems.［S.l.］:IEEE Press，2002:712－715.

［4］MIGUEL A C，MOHR A E，RISKIN E A.SPIHT for generalized multiple description coding［C］//Proc.International Conference on Image Processing.Kobe:IEEE Press，1999:842－846.

［5］KANG K，KIM T.Improved error control for real－time video broadcasting over CDMA 2000 networks［J］.IEEE Trans.Vehicular Technology，2009，58(1):188－197.

［6］BO Y，GHARAVI H.A hybrid frame concealment algorithm for H.264 AVC［J］.IEEE Trans.Image Processing，2010，19(1):98－107.

［7］DONOHO D L.Compressed sensing［J］.IEEE Trans.Information Theory，2006，52(4):1289－1306.

［8］CANDES E，ROMBERG J.Quantitative robust uncertainty principles and optimally sprase decompositions［J］.Foundations of Comput.Math.，2006，6(2):227－254.

［9］CANDES E J，TAO T.Near optimal signal recovery from random projections:Universal encoding strategies［J］.IEEE Trans.Information Theory，2006，52(12):5406－5425.

［10］DONOHO D L，TANNER J.Neighborliness of randomly projected simplices in high dimensions［J］.Academy of Sciences of USA，2005，102(27):9452－9457.

［11］BARANIUK R G.A lecture on compressive sensing［J］.Signal Processing Magazine，2007，24(4):118－121.

［12］CHEN S S，DONOHO D L，SAUNDERS M A.Atomic decomposition by basis pursuit［J］.SIAM Journal on Scientific Computing，1998，20(1):33－61.

［13］CANDES E J，ROMBERG J，TAO T.Robust uncertainty principles:exact signal reconstruction from highly incomplete frequency information［J］.IEEE Trans.Information Theory，2006，52(2):489－509.

［14］CANDES E.The restricted isometry property and its implications for compressed sensing［J］.ScienceDirect，2006，346(9):589－592.

［15］XU W Y，HASSIBI B.Compressed sensing over the grassmann manifold:a unified analytical framework［C］//Proc.2008 46th Annual Allerton Conference on Communication，Control and Computing.［S.l.］:IEEE Press，2008:562－567.

［16］STOJNIC M，XU W Y，HASSIBI B.Compressed sensing－probabilistic analysis of a null－space characterization［C］//Proc.IEEE International Conference on Acoustics Speech and Signal Processing.［S.l.］:IEEE Press，2008:3377－3380.

［17］MONAJEMI H，JAFARPOUR S，GAVISH M，et al.Deterministic matrices matching the compressed sensing phase transitions of Gaussian random matrices［EB/OL］.［2013－12－25］.http://www.pnas.org/content/110/4/1181.short.

［18］JON F.Decoding error－correcting codes via linear programming［EB/OL］.［2013－12－25］.http://hdl.handle.net/1721.1/42831.

［19］FELDMAN J.Using linear programming to decode binary linear codes［J］.IEEE Trans.Information Theory，2005，51(3):945－972.

［20］SMARANDACHE R，VONTOBEL P O.Absdet－pseudo－codewords and perm－pseudo－codewords:definitions and properties［C］//Proc.IEEE International Symposium on Information Theory.［S.l.］:IEEE Press，2009:229－233.