一种改进的LOFDM系统PAPR压扩变换算法

彭斯明，沈越泓，袁志钢，简 伟，苗誉威

(1.解放军理工大学通信工程学院，江苏南京 210007;2.济南军区通信网络技术管理中心，山东济南 250001)

网格正交频分复用(LOFDM)是由Strohmer和Beaver［1］于2003年提出的一种适合于在时频弥散信道上进行高速数据传输的技术，因其具有相比于传统OFDM技术更好的抗符号间干扰(ISI)和子载波干扰(ICI)能力，近些年来引起越来越多研究人员的关注［1－5］，但其PAPR性能的劣化却从另一侧面影响并制约着其实用性。

目前PAPR问题的处理方法主要有两类［6］，第一类是在信号经过快速傅里叶变换(FFT)之前进行的处理，如编码［7］、部分传输序列［8］、选择性映射［9］等，但是由于这些方法计算或实现复杂度较高，所以并不适合于实时性要求高的高速数据传输系统。第二类方法是信号在经过IFFT之后进行的处理，如限幅和滤波［10］、压扩变换［11－12］等，这些方法虽然往往会带来误码性能损失，但是由于其简单、有效、复杂度低的特点，相比之下更适合实时性要求较高的场合。而压扩变换因具有较限幅和滤波技术更好的性能而无疑成为抑制PAPR更为合适的选择。

为此，本文在将适用于传统OFDM系统的非线性压扩变换方法应用于LOFDM系统的同时，针对原有方法还存在灵活性不够的问题，研究并提出了一种改进的非线性压扩变换方法。通过在压扩函数中引入适当的参数从而简化了压扩变换中功率守恒的计算问题。所提出的方法不仅可以保证压扩变换前后功率不变，同时其计算复杂度、设计灵活性也得到进一步提升。仿真结果验证了本文方法的有效性。

1 系统模型及其PAPR

LOFDM系统在多个并行的正交子信道上传输数据符号，但是不同于传统的OFDM及脉冲成形OFDM(PSOFDM)，其各个子信道上符号的发送时刻并不是完全对称的。通常情况下奇偶序号的子信道上符号的发送时刻会错开一个符号周期［3］，图1给出了基本的LOFDM系统压扩变换原理框图。

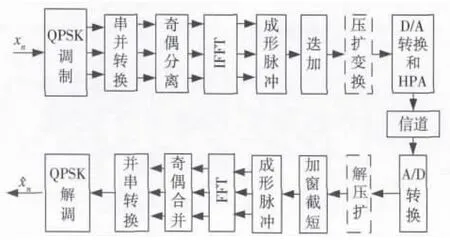
图1 LOFDM 系统压扩变换框图

含有N个子载波的LOFDM系统在n时刻的等效低通信号可表示为

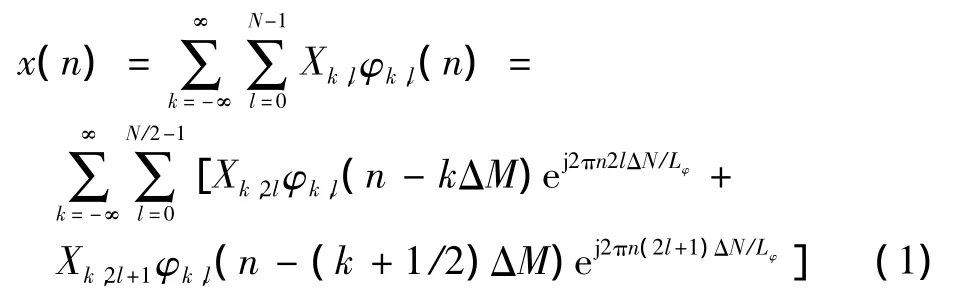
式中:φ(n)，n=0，1，…，Lφ－1为成形脉冲;Lφ是发送脉冲的长度;Δm，Δn分别为时间和频率间隔;Xk，l为待发送的数据符号。

通常，将LOFDM系统一个符号周期内信号功率的最大值与平均功率之比定义为信号的PAPR，其离散形式为

由于峰均比是个随机变量，其分布特性可以用互补累积分布函数(CCDF)来描述，它表示信号的峰均比超过某个门限的概率，即

式中:PAPR0为相应的PAPR门限。

2 算法设计

假设输入数据是独立同分布的，根据中心极限定理，当子载波个数足够大(N≥64)时，样值xn的实部和虚部满足均值为0的弱复高斯分布，幅度满足瑞利分布，其概率密度函数为

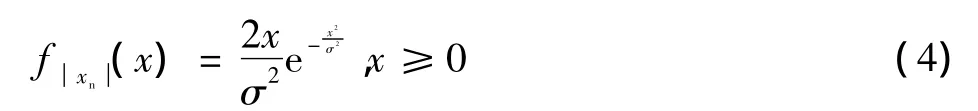
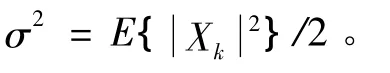
文献［11］中假设经压扩变换后信号的概率密度函数为

假设变换前后信号的功率不变，对于平稳的LOFDM信号则有

由式(6)知，c的取值是制约系统性能的关键。为了使c不受压扩前后功率守恒的制约，为此，在式(6)中引入一个新变量γ，使得当c取任意值时，等式(6)恒成立，即

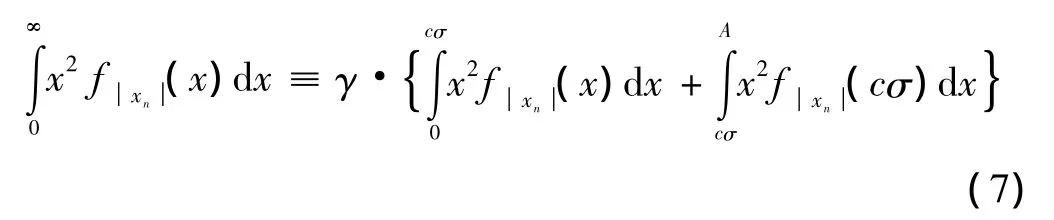
式中:

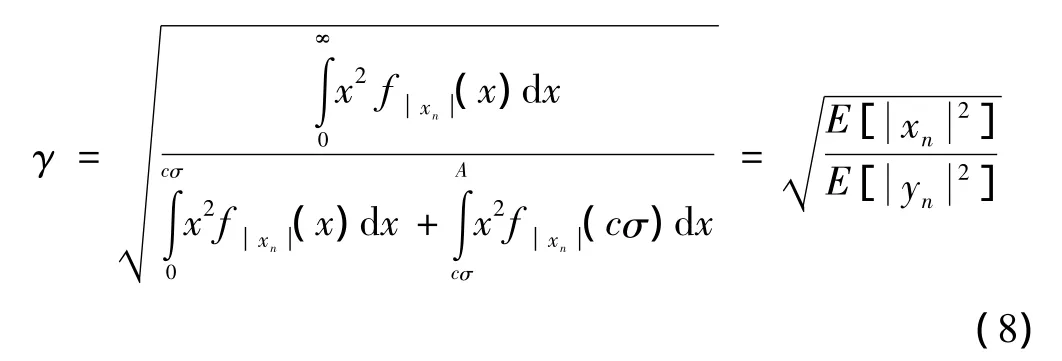
3 仿真试验与结果分析

为了验证算法的有效性，仿真过程中，子载波使用QPSK调制，仿真信道模型为AWGN信道，且仿真中假设系统的发射端和接收端是理想同步的，接收端不存在频偏。为了让本文提出的方法更加直观，仿真中未对LOFDM信号进行编码，同时仿真子载波数为N=64，各符号之间相互独立。

图2为不同压扩参数算法下的PAPR性能曲线。由图可见，原LOFDM信号的PAPR＞10 dB，当本文算法中c=1/时和文献［11］的所得到的PAPR累积分布曲线完全重合，这表明原方法只是本文方法的一个特例。当c=时，虽然本文方法较原方法PAPR损失0.8 dB，但是相比于原信号仍然有5.6 dB的改善。而当c=1/时本文的PAPR性能要较原方法改善0.26 dB。由于通常衡量一个压扩系统性能好坏除了PAPR性能外，误码性能也是一个关键，所以往往将两者联合起来考虑更为合适。

图2 不同c值下的PAPR分布

图3给出了LOFDM信号在AWGN信道条件下c取不同值时的误码性能曲线。由文献［11］可知，由于压扩变换往往会放大信道噪声，所以当接收端不进行解压时也能获得较好的误码性能。因此，仿真中对每个c值均同时给出了解压扩和无解压扩条件下的系统误码性能曲线。图中，“x”表示接收端未进行解压扩运算时的误码曲线。原信号的误码曲线可视为性能边界。由图可知，当c=1/时，采用本文给出的压扩变换和文献［11］给出的压扩变换后的误码性能曲线完全重合。对比图2可发现，虽然本文方法在c=1/时的PAPR性能优于文献［11］的性能，但是在Pe=10－5条件下，其所需的信噪比在接收端采用解压扩时较原方法高出0.2 dB，不采用解压扩时高0.3 dB;当c=1/时虽然PAPR性能要较原方法差，但在同样误码率条件下，在接收端采用解压扩时信噪比提高了约0.2 dB;而当c=时，在同样误码性能下当接收端采用解压扩时信噪比较原方法降低了2.25 dB，而不采用解压扩时和误码性能边界只相差0.59 dB。因此，采用本文算法后可以根据不同的系统性能需求灵活选择压扩参数。表1给出了不同压扩变化方法的性能比较结果。

4 小结

图3 AWGN信道下不同c值的误码性能比较

表1 不同压扩变换方法的性能比较

本文首先通过分析明确了传统压扩变换方法存在的问题及其产生的原因，然后在此基础上提出了一种改进的非线性压扩变换算法来有效抑制LOFDM系统的PAPR。通过引入一个合适的参数来简化压扩前后功率守恒中压扩参数的计算，该方法不仅保证了压扩变换前后的信号功率不变，同时其计算复杂度、设计灵活性也得到了进一步的提升。

:

［1］STROHMER T，BEAVER S.Optimal OFDM design time－frequency dispersive channels［J］.IEEE Trans.Communications，2003，51(7):1111－1122.

［2］YUAN Zhigang，SHEN Yuehong.A novel LOFDM signal and its optimization over doubly－dispersion channels［C］//Proc.IEEE Conference on Industrial Electronics and Applications.Singapore:IEEE Press，2008:853－856.

［3］简伟，沈越泓，李毅.基于广义Gabor变换的最优LOFDM系统的脉冲成形［J］. 电子与信息学报，2006，28(7):1274－1278.

［4］简伟.LOFDM系统性能分析及应用研究［D］.南京:解放军理工大学，2006.

［5］XU Kui，ZHANG Dongmei，XU Youyun，et al.Distribution of PAPR in LOFDM systems based on extreme value theory［C］//Proc.Wireless Communication and Signal Processing.Nanjing:IEEE Press，2011:1－5.

［6］韩艳春，杨士中.OFDM系统PAPR减小技术综述［J］.电视技术，2006，30(1):41－43.

［7］LI Li，QU Daiming.Joint decoding of LDPC code and phase factors for OFDM systems with PTS PAPR reduction［J］.IEEE Trans.Vehicular Technology，2013，62(1):444－449.

［8］QU Daiming，LU Shixian，JIANG Tao.Multi－block joint optimization for the peak－to－average power ratio reduction of FBMC－OQAM signals［J］.IEEE Trans.Signal Processing，2013，61(7):1605－1613.

［9］JIANG Tao，NI Chunxing，GUAN Lili.A novel phase offset SLM scheme for PAPR reduction in Alamouti MIMO－OFDM systems without side information［J］.IEEE Signal Processing Letters，2013，20(4):383－386.

［10］王兰勋，徐彬.PTS与限幅结合降低OFDM峰均比的改进算法［J］.电视技术，2009，33(9):79－81.

［11］HOU J，GE J，ZHAI D，et al.Peak－to－average power ratio reduction of OFDM signals with nonlinear companding scheme［J］.IEEE Trans.Broadcasting，2010，56(2):258－262.

［12］PENG Siming，SHEN Yuehong，YUAN Zhigang，et al.PAPR reduction of LOFDM signals with an efficient nonlinear companding transform［C］//Proc.IEEE Conference on Wireless Communications and Signal Processing.［S.l.］:IEEE Press，2013:1－6.