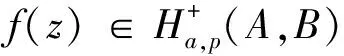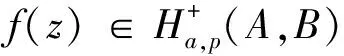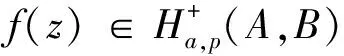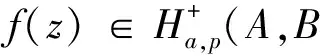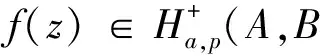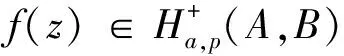由算子定义的一类亚纯p叶函数*
2014-09-17赵媛媛
赵媛媛
(江苏联合职业技术学院连云港中医药分院 基础部,江苏 连云港 222007)
0 引言
令Σp表示形如
(1)
且在D:={z:0<|z|<1}内解析的亚纯函数类.
对于f(z)∈Σp形如(1),g(z)∈Σp且
(2)
定义f(z)与g(z)的Hadamard积(卷积)为
(g*f)(z),(z∈D),
(3)
定义函数φp(a,c;z)为
(4)
(c≠0,-1,-2,…).
其中(x)k是Pochhammer记号,

对于f(z)∈Σp,利用函数φp(a,c;z),定义线性算子Lp(a,c):Σp→Σp,
Lp(a,c)f(z)=φp(a,c;z)*f(z).
(5)
若f(z)形如(1)给出,则由(4)与(5)可得
(6)
由(6)不难验证
z(Lp(a,c)f(z)′=
aLp(a+1,c)f(z)-(a+p)Lp(a,c)f(z).
(7)
利用算子Lp(a,c),对于固定的参数A,B(-1≤B (8) 则称f(z)在类Ha,p(A,B)中,也就是f(z)∈Ha,p(A,B). 另外,若f(z)∈Ha,p(A,B),且 (9) 下面先介绍Jack’s引理,后面的定理将运用此引理证明. 定理1若a>0,-1≤B Ha+1,p(A,B)⊂Ha,p(A,B). (10) 证明设f(z)∈Ha+1,p(A,B),并令 (11) 其中ω(0)=0,由(7)与(11)得 zp+1(Lp(a,c)f(z))′= (12) 这与f(z)∈Ha+1,p(A,B)相矛盾,所以|ω(z)|<1,(z∈D).则根据(11)得 所以f(z)∈Ha,p(A,B).定理证毕. 对于f(z)∈Σp,利用积分算子Jv,p定义函数Fv(z): Fv(z)=Jv,pf(z)= (13) 由(5)与(13)得 z(Lp(a,c)Fv(z))′= vLp(a,c)f(z)-(v+p)Lp(a,c)Fv(z). (14) 定理2定理条件同定理1条件,若f(z)∈Ha,p(A,B),Fv(z)如式(14)定义,则Fv(z)∈Ha,p(A,B). 证明令 (15) 其中ω(0)=0,利用(14)得 zp+1(Lp(a,c)Fv(z))′= (16) 余下定理证明与定理1方法类似,略. 在此部分内容中,总是设定-1≤B<0. (17) 结论是精确的. (18) 则 考虑z取实值,令z→1-,由(18)得 即 反之,若(17)成立,令|z|=1,由式(9)与式(17)得 结论对 (19) (k=p,p+1,p+2,…) 是精确的. 结论对(19)是精确的. (ⅰ) 若数列{Tk}是非降的,则 (20) (21) 则结论(20)(21)易得. (ⅰ)f(z)在圆|z| (22) (|z| 其中 (23) (ⅱ)f(z)在圆|z| (24) (|z| 其中 (25) 证明(ⅰ)由(9)可得 要证 (0≤ρ 即证 也即证 (26) 由(23)可得(26). 以下证明与(ⅰ)相同,略. 以上两结论对(19)是精确的. 参考文献: [1] RUSCHEWEYH S T. New criteria for univalent functions[J]. Proceedings of the American Mathematical Society, 1975, 49: 109-115. [2] GOEL R M, SOHI N S. A new criterion forp-valent functions[J]. Proceedings of the American Mathematical Society, 1980, 78(3): 353-357. [3] LIU Jinlin, SRIVASTAVA H M. Subclasses of meromorphically multivalent functions associated with a certain linear operator[J]. Mathematical and Computer Modelling, 2004, 39: 35-44. [4] JACK I S. Functions starlike and convex of orderα[J]. London Mathematical Society Series, 1971, 23: 469-474. [5] CHO N E. The Noor integral operator and strongly close-to-convex functions[J]. Journal of Mathematical Analysis and Applications, 2003, 283: 202-212. [6] LIU Jinlin. The Noor integral and strongly starlike functions[J]. Journal of Mathematical Analysis and Applications, 2001, 261: 441-447. [7] MACGREGOR T H. The radius of univalence of certain analytic functions[J]. Proceedings of the American Mathematical Society, 1963, 14: 514-520. [8] DZIOK J, SRIVASTAVA H M. Classes of analytic functions associated with the generalized hypergeometric functions[J]. Applied Mathematics and Computation, 1999, 103: 1-13. [9] 程艳莉,刘金林.一个线性算子及与之相关的亚纯多叶函数类[J].扬州大学学报:自然科学版,2004,7(2):10-12. [10] 杨定恭.关于具有变辐角的某些解析函数[J].苏州大学学报:自然科学版,1992,8(1):1-6. [11] 韦叶,秦涛.某一线性算子在亚纯多叶函数上的应用[J].淮海工学院学报:自然科学版,2010,19(3):1-4.
1 函数类Ha,p(A,B)
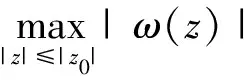

2 函数类