巧用夹逼准则求极限

高剑明， 叶海平

(东华大学理学院应用数学系，上海201620)

夹逼准则是高等数学中求极限的重要方法之一[1]. 它的适用范围涉及求数列的极限，一元以及多元函数的极限，反常积分的计算等等.近年来，全国大学生数学竞赛试题中也频频出现它的身影. 本文旨在巧用夹逼准则求各类极限. 通过归纳和分类，帮助学生掌握夹逼准则适用的类型和相关的解题技巧.

1 求数列的极限

[类型一]简单放缩.

错误分析 在上述运算中，使用了极限运算法则“和的极限等于极限的和”，这个运算法则只对有限个函数之和的情形才成立. 但在本题中，随着n趋于无穷大，函数的个数也趋于无穷大，所以该解法是错误的. 正确解法是用夹逼准则.

解由于

[类型二]适当放缩.

以定积分形式表示的数列，该定积分难以算出精确表达式，常用夹逼准则求该数列的极限.这里，放大、缩小要适当，两头极限必须相等才行. 因此，如何适当放缩是难点.

证因为

而

根据“夹逼准则”可知，

[类型三]放缩后，再利用积分和.

适当放缩后，经常可以变为积分和[2]，即利用

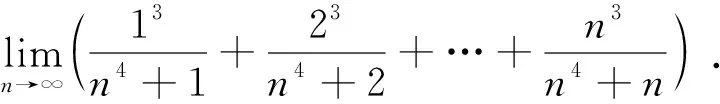
[类型四]化乘积为求和.

取自然对数，可使n项乘积变为n项求和. 然后再用夹逼准则求n项和式的极限.

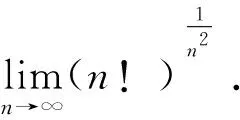
又

由夹逼准则，得

故原式=e0=1.

2 求一元函数的极限

[类型五]函数取绝对值后放大.

解因为x>1时，

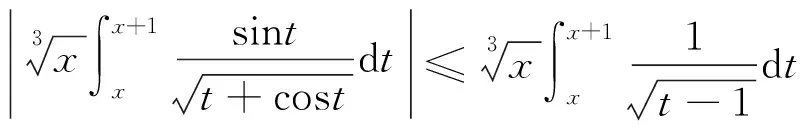
所以

[类型六]用数列夹逼函数.

以积分上限表示的函数，常用数列两边夹该函数，然后再用夹逼准则求得该函数的极限.

解对于任何足够大的正数x，总存在正整数n，使nπ≤x<(n+1)π，这样x→+∞就等价于n→∞，所以

而

所以

3 求无穷区间上的反常积分

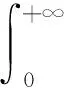
解当nπ≤t<(n+1)π时，t→+∞等价于n→∞，

而

同样

由夹逼准则，得

4 求多元函数的极限

将多元函数自变量记为一个向量P=(x1,x2,…,xn)，则多元函数u=f(x1,x2,…,xn)就可以写成u=f(P). 夹逼准则是证明极限为零的常用方法. 若估计所求极限为零，可采用不等式方法放大，

0≤|f(P)|≤g(P)，

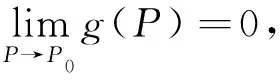
解由于

[参 考 文 献]

[1] 同济大学应用数学系. 微积分[M]. 北京：高等教育出版社，2002.

[2] 李绍宽. 高等数学学习指导书[M]. 上海：东华大学出版社，2000.