电子设备方舱热学分析/*
2014-09-16毛勤俭姬永清
毛勤俭,姬永清,吉 芸
(中国电子科技集团公司第二十八研究所, 江苏 南京 210007)
电子设备方舱热学分析/*
毛勤俭,姬永清,吉 芸
(中国电子科技集团公司第二十八研究所, 江苏 南京 210007)
电子设备方舱热设计对机动式指挥通信系统的可靠性影响很大,而现行的方舱热设计方法存在缺陷,不能准确计算方舱所需的能耗。文中分析了现行热设计计算方法的不足,通过对方舱进行热学动态特性分析,推导出更为精确的计算公式,可提高电子设备方舱的热设计水平。
传热系数;比热;热平衡
引 言
近年来,机动式通信系统和指挥系统在军用和民用领域得到迅速发展和普及。通信系统和指挥系统主要由电台、卫星收发机、计算机、交换机等电子设备组成。承载这些电子设备的平台越来越多地选择具有保温隔热、电磁屏蔽等功能的方舱。对方舱温度调节所需的加热和制冷功率,许多方舱设计人员已进行过研究,本文对此项工作再作讨论,提出一些新的结论,供本专业人员参考。
1 电子设备方舱热学要求
由于电子设备大多属于热敏感设备,即设备的工作温度只能局限在某一区域内,超出此温度区域就会影响设备和系统的可靠性[1],所以电子设备方舱不仅要具有保温隔热功能,还要求配备空调、燃油加热器等设备,从而使方舱具有温度调节功能。
结合相关军用标准和用户使用要求,对电子设备方舱的热学性能要求归纳如下:
1)方舱隔热性能以传热系数(热流密度)表示,有3个等级即1.5 W/(m2·℃), 2.0 W/(m2·℃)和 2.5 W/(m2·℃),这个要求由方舱结构尤其是大板隔热层保证[2]。
2)当舱外温度为-30 ℃时,要利用采暖设备,在30 min内将舱内温度升至0 ℃以上。这时需要为方舱配置采暖设备,并设计适当的功率。
3)当舱外温度为40 ℃时,要利用制冷设备,在40 min内将舱内温度降至30 ℃以下。这时需要为方舱配置制冷设备,并设计适当的功率。
本文假定方舱的第一项要求即隔热性能达标,仅讨论用于方舱温度调节的采暖设备或制冷设备所需功率的计算方法。
2 目前常用算法的缺陷
2.1 热平衡的算法
假设方舱的保温性能达标,舱外温度为寒冷,舱内需加热,其传热系数为λ,舱内外温差为T,加热器功率为Q(含舱内设备发热量),方舱舱壁面积为S,则从舱壁传出的热量为
Q1=λST
(1)
如果进行粗略计算,当温差为T时,只需舱内加热设备补充与Q1相等功率的热量,即可使舱内达到热平衡,这是目前常用的一种算法[3]。但是,对于有些方舱,并不是达到了热平衡就可以满足要求的,还需要在限定时间内将方舱温度提升至要求的温度,此时按式(1)计算显然是不够的,还应加上提升方舱温度所需要的功率。
2.2 热平衡与温升功率之和的算法
提升温度消耗的热能与比热有关,比热的物理概念是将物体温度提高1 ℃所消耗的热能,不同材料比热不一样。因此,提高方舱温升的计算应考虑舱内所有设备和方舱部分材料的比热以及舱内空气比热,分别计算温升消耗的热量,求其和,再除以限定的时间,得到提高温升所需的功率。但如此计算过于复杂,通常设方舱内材料的平均比热为C,在限定时间t内将质量为m的方舱设备的温差提高T度所需要的功率为
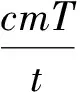
(2)
由此可得加热设备的总功率为
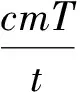
(3)
这样计算即考虑了热平衡又考虑了方舱温升,基本可以满足一般设计要求,是目前常用的第2种算法。
但是如果进行仔细分析,这种算法还是不准确。例如,当温度升高到指定工作温度时,热量的传导损失依然存在,需要补充与Q1相等的热量以保持方舱的热平衡。但使舱体和设备继续升温的热能不再需要,也不能再有了,否则温度将会继续升高。由此可见,按式(2)计算所得的功率会大于实际所需的功率。
3 热学微分方程及其解
如果要更准确地计算方舱加热设备的功率,需要将方舱的热学变化过程看成是一个动态的过程。初始时,舱内与舱外温差为零,热传导损失为零,在这一瞬间,加热设备的热功率全部消耗在升温上;在加热初期,温差较小,热传导消耗亦小,加热设备的热能小部分消耗在热平衡上,大部分消耗在升温上,所以此时方舱温升比较快;在加热后期,温差比较大时,热传导损耗变大,大部分热能消耗在热平衡上,少量热能贡献给了温升,这时温升较慢,而且越来越慢;当达到指定温度时,温差达到最大值,全部热能用于热平衡,舱内温度不再升高。经验表明:舱内温度T与时间t的关系是一条前陡后缓的渐近线,如图1所示。

图1 舱内温度T与时间t的关系
为了更清楚地了解方舱热学变化过程和准确地计算方舱加热设备的功率,需建立方舱热学微分方程并求解。
设温差变量为T,时间变量为t,初始温度即舱外温度为零点,舱内热能功率为Q,热能功率Q减去温差热损耗后的剩余热量使舱内温度升高,则据此建立以下微分方程:
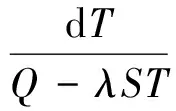
(4)
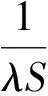
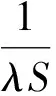
(5)
两边积分得
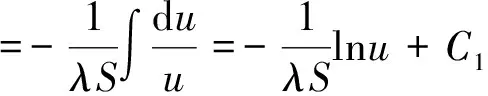
(6)
将u=Q-λST代回式(6)得:
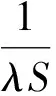
(7)
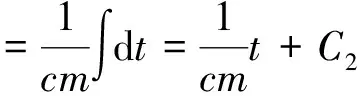
(8)
左=右,并令C3=C2+C1,则
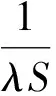
(9)
令C=-C3λS,则
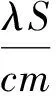
(10)
由原始条件当t=0时,T= 0(温差为零),则有C=lnQ,代入式(10)得
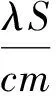
(11)
即
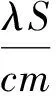
(12)
由对数指数概念得:
(13)
或

(14)
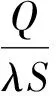
当加热时间和舱内温度升高值确定时,则可按照式(14)计算加热设备的功率,可见所需功率Q值将大于热平衡所需功率。
4 结束语
通过建立微分方程并导出式(13)和式(14),进一步明确了方舱温度调节的动态过程和热能分配,可以用于电子设备方舱的热学计算。以上推导过程,虽然是以舱内升温过程为例进行推导的,但其结果同样适用于舱内使用制冷设备的降温过程。
[1] 邱成悌, 赵惇殳, 蒋全兴. 电子设备结构设计原理[M]. 南京: 东南大学出版社, 2001.
[2] 国防科学技术工业委员会. GJB 870—1990 军用电子设备方舱通用规范[S]. 北京: 国防科工委军标出版发行部,1990.
[3] 江红.军用通信方舱的取暖和制热设备选择[J]. 指挥信息系统与技术, 2011, 2(4): 76-78.
毛勤俭(1957-),男,研究员,主要从事机动式指控系统结构总体设计工作。
Thermal Analysis of Electronic Equipment Shelter
MAO Qin-jian,JI Yong-qing,JI Yun
(The28thResearchInstituteofCETC,Nanjing210007,China)
The thermal design of the electronic equipment shelter has a great effect on the reliability of command and communication system. The traditional thermal design calculation method cannot calculate the energy needed by the shelter accurately. The deficiency of the existing thermal design calculation method is analyzed in this paper. The more accurate calculation formula is derived by the thermal dynamic characteristic analysis of the shelter, which can be used to improve the thermal design level of the electronic equipment shelter.
heat transfer coefficient; specific heat; thermal balance
2014-01-03
V243
A
1008-5300(2014)03-0024-03
