基于激光雷达点云的树冠分形维数及其算法实现

郑莎莎 ZHENG Sha-sha；吕毅斌 LV Yi-bin

（昆明理工大学理学院，昆明650500）

0 引言

Mandelbrot（1975）[1]正式提出与建立的分形理论，主要研究分形体的维数及自相似性规律[2]，分形维数是分形几何的核心，通过计算分形维数，可以对不规则的自相似几何形体（如植被根系、树木分枝结构、树冠、叶片分布特性及种群分布格局等）的复杂程度进行定量分析[3-6]。树冠作为树木自身遗传特性和环境影响的综合体，决定着林木外部形态以及对光能的截获、水分和养分的分布，既是树木生长发育的结构基础，又直接影响种群的三维空间分布格局。此外，不同的树种本身的树枝、叶片分布情况也不尽相同。前人研究表明林冠结构的复杂性和动态是影响森林生态系统结构和功能的主要因素之一，分形维数反应复杂形体占有空间的有效性，它是复杂形体不规则性的度量。所以文中以激光雷达点云数据为基础，计算单个树冠的三维空间的分维数。本文从分维角度细致解析树冠的分维结构为进一步研究不同树冠分形维数测算提供依据、经营与管理。

1 数据及研究方法

1.1 数据来源 利用地面三维激光雷达扫描仪Reigl VZ-1000进行单站点扫描，数据格式存储为LAS格式，对获取的点云数据进行裁剪，只保留树冠部分的信息。

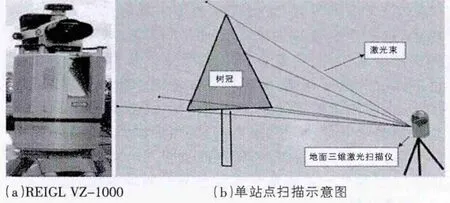
图1

1.2 数据预处理 激光雷达点云数据属于维数等于3维的数据集，数据文件为las格式的文件，数据是海量级别的，单棵一般的树冠包含几十万个点，数据量太大，再进行相关的研究时，计算会耗费大量的时间，而这样做事没有必要的。故先对数据进行抽稀处理，抽稀方法为：先进行一定的随机抽稀处理，再采用格网抽稀法进一步抽稀，从而简化树冠点云数据。先将LAS格式的二进制文件点云数据转化为所需的文本文件TXT格式，再利用MATLAB软件进行算法实现。数据预处理步骤如下：

①利用ENVI软件的扩展功能BCAL LiDAR读取原始LAS格式的二进制文件点云数据，并将其存储为shp格式输出；

②在ArcGIS10.0中读取(1)中输出的shp文件，打开相应的属性表，将其转储为txt文件格式并输出；

③在MATLAB中读取2)中txt格式的点云数据，同时利用自编的MATLAB程序对读取的点云数据进行抽稀处理，处理后的结果保存到一个F中，文中后续的计算都是以F为研究对象。

图2所示的三棵树冠点云，分别呈现了经过上述预处理后点云的分布情况。注意，三棵树冠均属于不同类型的树种，它们不仅冠形率不同，树冠内部结构分布也不同。

图2 树冠点云数据

表1 树冠参数

图3 ln(S(δ))与 ln(δ)的关系图

1.3 树冠分形维数的计算 点云树冠的分形维数D就是计算树冠点数据集的分形维数。根据吴新玲和周国强（2011）[7]提到的数据集分形维数的计算方法，采用计盒维数法计算点云树冠的分形维。计盒维数是目前应用最普遍的分形维数之一，计算分形维数的数盒子方法，又称为覆盖法，它适用于简单分形，也适用于复杂分形。实践中计算D最常用的方法就是采用计盒方式。数盒子法的实质是改变粗视话程度。对图形进行测量，通常先从数大盒子开始，一次减小盒子的尺度，只计算那些“非空”盒子数。越不光顺、越不规则的图形具有更大的分维。图形越规则，越光顺，其对应的分维就越小。对于空间数据集来说也是如此。即将点云数据F所在的三维空间划分为δ边长为的三维格网单元，计算格网中每个单元包含的数据点数，假设树冠点云数据集为F，Sδ（F）是δ下F的测量值，即

此时Sδ（F）表示覆盖F的边长为δ的立方体盒子的个数。由于假设数据集是自相似集，那么s可以通过δ在一个有限的范围（δ1，δ2）内lnSδ（F）与lnδ形成的双对数图对应直线部分的斜率来估算。其常量斜率即为F的盒维数Dδ（F）。算法步骤如下：

①计算树冠点云的最小包围盒，划分三维格网，格网尺寸为0.05m；

②对F中每个数据点d，作尺寸r从1到30的盒子，分别计算非空盒子的个数Sδ（F）；

③对 δ=0.05*r分别计算 ln（δ）；

④生成ln（Sδ（F））与ln（δ）的双对数图；

⑤D是图中直线部分的斜率；利用最优六分割法提取曲线中的最长直线部分。

计算结果呈现在图3。图2中的(a)、(b)、(c)分别对应三个树冠点云数据集的双对数图。

三棵树冠的分形维数情况如下：

D1=2.2605；D2=2.3025；D3=2.0393。

2 结果与分析

分形维数越小，表示树冠内部分布越光顺和规则。格网划分尺度越细精度越高，r的尺度变换较缓时比变化较快时盒维数D的精度高。三棵树冠分形维数的对比可知：分形维数越高，树冠的分枝结构越复杂，其占据和利用生态环境空间的能力越强。具有比较典型的分形特征，分形维数是否独立于尺度。个体树冠具有自相似性，可用分形维数来刻画其结构特征，以统计空间填充能力为基础的树冠分数维度值为：盒维数与冠型的关系，分形维数较高，揭示出其分枝结构十分复杂。三棵树冠的分形维数关系为：D2＞D1＞D3，结果符合实际，从真实的树冠和点云数据显示可看出树冠(b)确实是最不光顺的和最不规则的。

3 结语

分形维数是分形几何在许多领域应用的测评工具，采用数盒子法计算分形维数是常用方法，理论简单易于实现，因此利用它的计算点云树冠的分形维数是方便的。本文以点云数据形式的树冠为对象，计算其盒维数，实验数据表明：利用双对数图估算树冠点云数据集的分形维数是有效的。

[1]Kenneth F.分形几何数学基础及其应用[M].北京:人民邮电出版社,2007.

[2]刘琼,李世银,王秀娟.自相似网络流量建模及分析[J].微电子学与计算机,2009,25(11):131-134.

[3]娄莉,刘天时.基于小波与分形相结合的图像压缩优化算法[J].微电子学与计算机,2010,27(6):145-148.

[4]Traina C,Traina A,Wu L,et al.Fast feature selection using fractal dimension[J].Journal of Information and data Management.2010,1(1):1-15.

[5]Belussi A,Faloutsos C.Estimating the selectivity of spatial queries using the Correlation Fractal dimension[J].Proceeding s of the 21st international conference on very large data bases,1995(2):299-310.

[6]So usa E P M,Traina C,Tr aina A J M,et al.A fast and effective method to find correlatio ns among attributes in databases[J].Data Mining and Knowledge Discovering,2007(14):367-407.

[7]吴新玲,周国强.数据集的分形维数及其算法实现[J].微电子学与计机,2011,28(6):12-15.