重力坝坝踵等效应力法

王春涛 WANG Chun-tao；邹时华 ZOU Shi-hua

（南昌大学科技学院，南昌330000）

0 引言

目前大坝的应力分析主要有材料力学方法和弹性力学方法，材料力学方法由于没有考虑坝体和地基的相互作用，其应力解在地基以上30%的范围内不可靠，弹性力学方法（一般用有限元法得到数值解）在坝体的大部分区域的应力解答都比较准确，只是在坝踵、坝趾部位由于应力集中影响，其应力解答失真。所以按弹性力学方法，只要确定了坝踵、坝趾的应力分布，则可以知道整个坝体的应力分布。而坝趾和坝踵的受力状态不同，因为坝趾受到的是压应力，当其压应力超过混凝土抗压强度时，由于混凝土的塑性应力重分布使坝趾应力降低而不至于开裂。即使坝趾区开裂，也可以形成稳定裂缝，不至于影响大坝安全[1]。所以问题的核心是确定坝踵处的应力大小。

1 现有的坝踵应力问题的研究方法和不足

按弹性力学理论坝踵区由于应力集中，其应力理论解为无穷大。所以应用有限元法计算坝踵应力，会出现随着网格加密应力逐渐增大的现象，这是随着网格加密逐步逼近理论解产生的。对此问题人们做了很多研究，得出了很多有用的结论，主要有：对于各种网格划分方案，各种坝的平均相对拉力区长度基本不变[2]；有限元计算结果在距离坝踵角点1%～2%H的范围以内应力失真，在此之外其应力解答可满足要求[3]。据此，有人提出了以坝踵附近位置的应力代表坝踵处应力的方法[3]。即：以坝踵角点为圆心，以1%～2%H为半径，在此圆周上的一圈应力代表坝踵处的应力。这样就可以简便的得到坝踵（等效）应力。

该方法的合理之处在于：①在很小的尺度内混凝土不能看做是均质弹性材料，因此费大力气找出坝踵这个点处的应力没有意义；②混凝土的强度也是在一定尺度下试验获得，即使得到了一个点处的应力，也无法跟混凝土强度比较。所以，应该把求一个点处的应力转变为求坝踵一定区域内的应力。

这种方法为研究坝踵应力提供了新的途径，即不再费力求解坝踵区的精确应力，而以应力代表值（等效值）来代表坝踵区应力，这可能是以后研究坝踵应力的发展方向之一。但这种方法也有不足之处：①忽略了应力集中的影响。尽管坝踵处的应力不会像理论上为无穷大，但毕竟应力集中是存在的，坝踵处的应力应该比其它部位有突变；②不满足静力平衡条件。图1表示某一重力坝沿建基面的正应力分布，图1.1表示由有限元法计算所得的应力分布，图1.2为应力等效方法所得的应力分布，在只承受静水压力和自重时，建基面上正应力的代数和等于坝体的重力，即阴影部分之和（矢量和）等于坝体的自重。很明显图1.2代表的近似方法所得的应力分布不满足静力平衡条件。

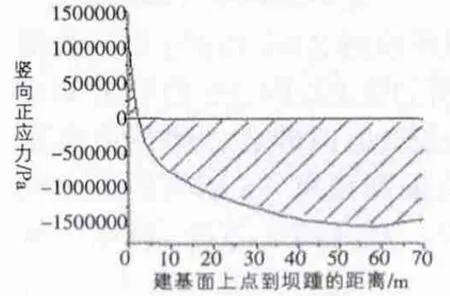
图1.1 有限元计算所得建基面的正应力分布

图1.2 近似方法所得的建基面正应力分布

2 坝踵等效应力法

坝踵应力应能满足静力平衡条件且考虑到坝踵应力集中的影响，可把由离开坝踵1%～2%H处的应力代表坝踵应力改为由坝踵区域的平均应力代表坝踵应力。平均应力可由图1.1中坝踵区域的应力面积除以坝踵区域长度得到。此方法可称为坝踵等效应力法。

坝踵应力等效法的正确性需要受到验证，为此建立如图2所示的有限元模型：坝高为100m，下游坝面坡度为1:0.7，上、下游地基长度取200m，地基深度为200m，上、下游地基取水平约束，地基底面为固定端，坝体受到上游面静水压力和自重作用，且上游河床受到静水压力，不计入扬压力。混凝土弹性模量取2100Mpa，密度取2400kg/m3，地基弹性模量取2100MPa。单元划分方案为：在建基面上由疏到密分为 P1、P2、P3、P4、P5五种方案。在距坝踵角点2m的范围内单元个数分别为 1，2，4，8，16。计算模型如图2所示。

图3是计算后得到的竖向正应力分布，图中仅截取了距坝踵3m范围内的应力分布。可以看出，在距离坝踵2.5m以外，五种方案结果一致，在距离坝踵1m以外，P2、P3、P4、P5四种方案应力分布基本相同，而在距离坝踵1m以内各方案的应力相差较大。所以需重点研究距离坝踵角点1m以内的应力变化，将此范围内称为坝踵区域。在坝踵区域内，有以下特点：①在距离坝踵1m之内，竖向正应力离散性很大，五种方案的竖向正应力最大值分别是 0.35、1.25、2.20、3.59、5.42Mpa。②方案P5的网格最密且坝踵应力最大，但方案P5的应力曲线部分落在其它方案的应力曲线之下，即各种方案的应力分布曲线相互交叉。说明并不是网格越密，坝踵区所有位置的应力都越大，而是随着网格加密，坝踵角点的应力急剧增大，而坝踵区域其它点的应力有减小的趋势。

图2 重力坝计算简图

把应力分布曲线与直线y=0形成的面积称为应力面积。对计算数据分析可知P2、P3、P4、P5四种方案坝踵区域的应力面积（总拉力）分别是930kN，1410kN，1750kN和1960kN，由此得出坝踵区域的应力平均值分别是0.93MPa，1.41MPa，1.75MPa，1.96Mpa，如图 4 所示。相对于坝踵应力值来说，P3、P4、P5方案的平均应力值已经很接近了，说明用此方法可以得到比较稳定的坝踵平均应力值。

3 结语

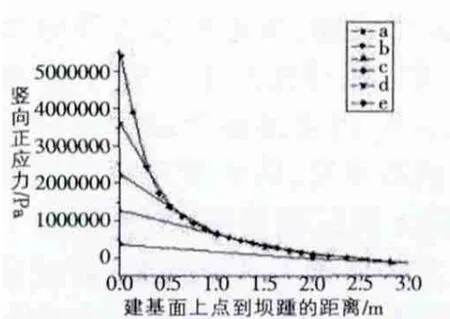
图3 有限元计算得到的五种方案竖向正应力分布图

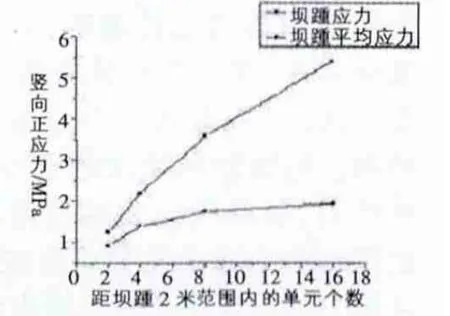
图4 坝踵应力随单元的变化趋势

文中以坝踵处竖向正应力为例研究了坝踵应力等效方法，是因为建基面一般比较薄弱，一般竖向正应力决定了坝踵是否开裂。同样地，对其它应力分量也可以这样确定坝踵应力，作为判断坝踵是否会开裂的依据。当坝踵等效应力超出混凝土抗拉强度时，则认为坝体会产生裂缝，形成新的边界，此时应按边界改变后的模型重新计算，其坝踵应力还可以用坝踵等效应力法计算，以考察坝踵是否会形成新的裂缝，如此重复，直到裂缝稳定为止。

本文通过总结以坝踵角点附近的应力作为坝踵角点的应力的方法，提出了以坝踵区域的平均应力做为坝踵代表应力的坝踵等效应力法。这种方法可以得到比较稳定的坝踵应力值，解决了坝踵应力随网格的变化而变化的问题，而且它既能反映坝踵区域的应力集中，又能反映结构的静力平衡条件，具有明确的物理意义且计算简便，是一种较为实用的方法。

[1]潘家铮.重力坝设计[M].水利电力出版社,1987.

[2]赵代深.重力坝有限元计算网格剖分与应力控制标准问题[J].水利学报,1996（5）.

[3]敖麟.重力坝坝基附近的应力分布及有限单元法解答[J].水利学报,1984(8).