中心折反射相机标定方法综述*

2014-09-14赵丽娜胡万宝

计算机工程与科学 2014年5期

关键词：抛物球面摄像机

张艳,赵丽娜,胡万宝

(北京化工大学理学院，北京 100029)

中心折反射相机标定方法综述*

张艳,赵丽娜,胡万宝

(北京化工大学理学院，北京 100029)

近十几年来，计算机视觉越来越受研究者们的欢迎，特别是全景相机由于其具有较大的视场而被广泛应用到许多领域，包括视频监控、机器人导航、电视电话会议、场景重建以及虚拟现实等。摄像机标定是从二维图像获得三维信息必不可少的一步，摄像机标定结果的好坏直接决定着三维重建结果以及其它计算机视觉应用效果的好坏，所以，研究摄像机的标定方法具有重要的理论研究意义和重要的实际应用价值。这里将2000年到2012年折反射相机标定方法按照标定像的不同分为五大类：基于线的标定、基于二维标定块标定、基于三维点的标定、基于球的标定和自标定，且简要分析其优缺点。

球面模型；折反射；相机标定

1 引言

计算机视觉的研究目标是使计算机具有通过二维图像认知三维环境信息的能力。这种能力不仅使机器能感知三维环境中物体的几何信息，包括它的形状、位置、姿态、运动等，而且能对它们进行描述、存储、识别与理解。

从二维图像恢复三维物体可见表面的几何结构的过程称为三维重建。三维重建主要分三个步骤完成：(1)图像间对应点的匹配；(2)标定内参；(3)求解外参数。

最早研究的全景相机技术有旋转拼接式和鱼眼摄像机，但是由于系统中存在转动机构,系统的实时性很难得到满足,在实时性要求较高的场合无法应用。而鱼眼摄像机系统复杂,造价昂贵。1999年Baker S和Nayer S[1]提出折反射系统由一个传统相机及正前方的一个反射镜面组成，并将其分为两大类：中心系统与非中心系统。并且给出了中心折反射系统的完全分类：抛物折反射——正交相机前面放一个旋转抛物镜面；双曲折反射——透视相机前面放一个旋转双曲镜面；椭圆折反射——透视相机前面放一个旋转椭圆镜面；平面折反射——透视相机前面放一个平面。单视点全景折反射成像系统满足单视点约束而且增大了视场，其中单视点比较适合建立数学模型，很容易计算相机的入射光线方向，而大视场可以帮助我们缩小局部视图的可能性，提取特征。2001年，Geyer C和Daniilidis K[2]给出了球面统一模型，其具有良好的几何约束，适合于建立统一的模型，图像特性也更加方便研究。

传统相机标定是一个线性问题，折反射相机标定是非线性问题，研究者们研究折反射相机标定的热点就是试图寻找线性解法。本文第2节介绍球面成像模型及镜面分类；第3节介绍标定方法分类，并对其中的五个方法进行详细的方法介绍，也是本篇文章的主要部分；第4节为本文小结。基于球面的折反射相机标定仍是一个富有挑战性的问题。

2 球面模型

折反射全景成像系统由一个常规的相机和一个反射面构成。Svoboda T等人[3]证明了不同镜面对应不同的模型而且给出了对极几何相关的公式。Geyer C和Daniilidis K[4]提出了可以处理任何中心折反射系统的统一模型：球面相机模型(图1)，后来该模型被Ying X[5]和Barreto J P[6]推广，迄今为止球面模型仍被广泛应用。

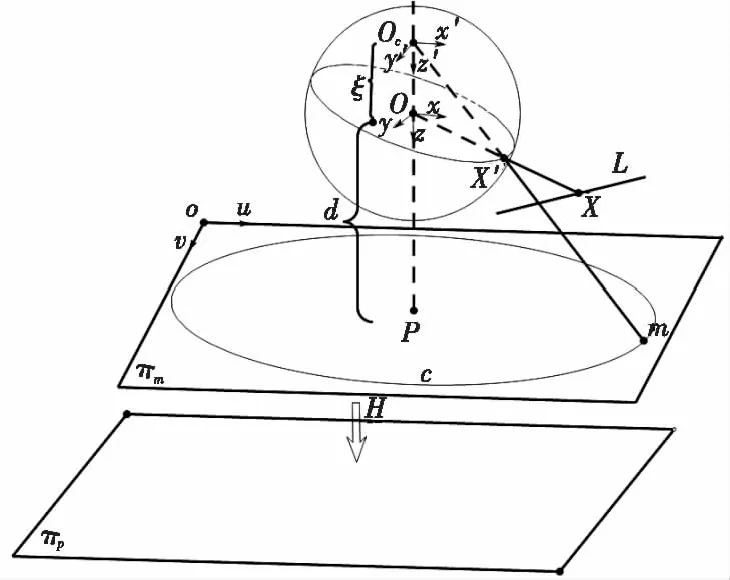
Figure 1 Spherical camera model图1 球面相机模型

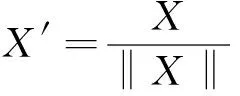
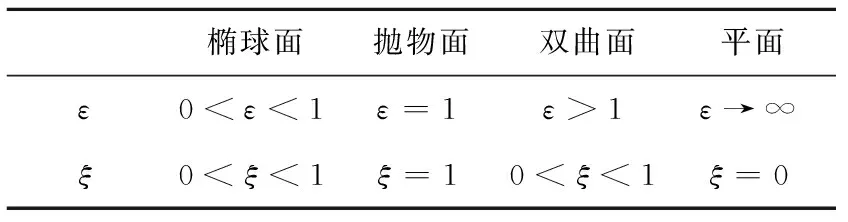
Table 1 Catadioptric camera category

3 标定方法分类

关于标定方法的分类已在文献[5,7～9]中给出，Deng X M[7]将方法分为自标定、基于球、基于线、基于点、二维标定方法。Duan H等人[8]将标定方法分为自标定、基于三维点的标定、基于二维点的标定、基于线的标定、基于球的标定。Ying X H等人[5]把标定方法分为已知世界坐标系、自标定、线的投影。Puig L等人[9]按照标定系统的主要性质将标定方法分为基于线的标定、二维模式标定、基于三维点的标定、自标定、配极(Polarition)成像。本文按照有无标定块将方法分为两类：有标定块；无标定块,即自标定。其中有标定块按照其标定块的不同分为：基于线的标定、基于二维标定块标定、基于三维点的标定、基于球的标定。因此本文将标定方法分为上述五类。

3.1 基于线的标定

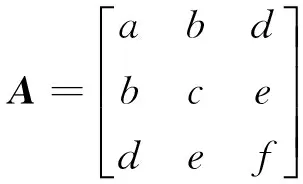
(1)

(2)

其中n=(nx,ny,nz)为球面像所在平面的法向量。由几何不变量得到空间线的三个约束：

L1=d(bd-ae)-e(be-cd)=0

(3)

(4)

(5)

球的两个约束：

s1=d(bd-ae)-e(be-cd)=0

(6)

(7)

得到参数的约束方程，利用三个球或者两条线即可标定相机。此方法基于球的标定比基于线的鲁棒性更强，精度更高，但是当镜面参数未知时，不能确定焦距，而且不适用退化的情况。2005年Barreto J P和Araujo H[11]研究了线的像的投影不变量性质，证明了任意中心折反射相机均可由三或三条以上的线的像标定。Ying X H[12]等人提出了运用Hough变换来探测线的像，标定相机。2008年Wu F C等人[13]找到了一个适用于所有折反射相机的线性方法，首先提出空间点在可视球上的投影XS与其折反射像m之间的关系:

(8)

其中τ=(1-ξ2)/ξ2，ω=K-TK-1,m是一个三维行向量，得出主点约束方程:

(9)

运用三条线的像求出主点；平移像平面的原点到主点，得到空间线折反射投影标定参数的一组约束:

(10)

最后在无任何相机先验信息的情况下，通过一个视点下的三条或者三条以上的直线得到线性约束方程求解ω和τ的值。此方法不但提高了标定的稳定性，而且除了主点以外，所有参数都可以同时估计。

这类方法不需要知道用于标定的空间直线间的相对位置以及直线相对于摄像机的位置关系，但只能估计摄像机内参数，不能估计外参数。但是，基于线的像的标定在实际中很难应用，因为需要从一小弧来拟合二次曲线，这样标定既不准确也不可靠。而且一般情况下，如果涉及很多线很难找到二维—三维对应，因为并不是所有的二次曲线都是线的像[14]。Barreto J P和Araujo H[15]找到了拟合抛物折反射线像的二次曲线的充分条件,并且给出了证明。

3.2 控制点的二维标定模式

这些控制点可以是角点、边界点等任意易获取的点，运用迭代的方法恢复内参数和外参数。2004年，Wu Y H等人[16]运用同一个平面或者两个平行平面内的两个圆进行标定。步骤简述如下：两个平行圆与透视投影像之间建立拟仿射不变量，通过圆环点的像找到相机内参的线性约束:

(11)

(12)

此方法精度高，鲁棒性强，而且需要的标定物的数量小(只需两个平行圆)。2007年，DengXM等人[7]利用折反射相机三维椭圆边界的像:

au2+2buv+cv2+2du+2ev+f=0

(13)

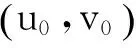
(14)

焦距fe表达式为:

(15)

然后使用中心折反射模型和球面模型之间的关系，运用DLT算法计算外参数初始值，再用非线性化的方法重新定义除主点以外的内、外参数，其优点是无需拟合部分可见二次曲线，仅需标定图像的椭圆边界和二维标定模型的像，而且此方法对于针孔模型和所有中心折反射相机来说标定简单。2009年Gasparini S等人[17]用一个二维—二维对应的单应阵H坐标提升为6×6矩阵:

(16)

最少12对匹配点，运用DLT-like即可算出单应阵，三幅图像的单应即可恢复IAC。对于抛物折反射相机而言，单幅图像即可标定。

3.3 基于三维点的标定

基于三维点的标定，只需知道三维空间点坐标，即可标定折反射相机。该方法的优点在于标定精度高，但是需要精度很高的标定块。

2001年Aliaga D G[18]放宽抛物折反射系统的假设，找到控制点的三维坐标与其二维图像坐标的对应关系，估计焦点距离使其满足针孔模型，运用最优化环来拟合内参数和外参数。2004年，Vasseur P[19]提出了一个非线性方法来标定相机内参数。2005年，Wu Y H[20]等人找到一维/二维/三维场景点的不变量方程来拟合线性估计主点。2007年，Deng X M[21]等人又提出了三维空间中位于同一条直线的上的五个点在进行三次或者三次以上的简单刚体变换以后，通过其图像所隐含的消隐点线性求解IAC，即可标定折反射相机的参数。2010年，Puig L等人[22]提出一种基于类直接线性算法(DLT-like)。

具体算法如下:三维点Q=[Q1Q2Q3Q4]T、像点q=[q1q2q3]、三维—二维对应投影矩阵P提升标：

(17)

(18)

(19)

其中：

(20)

3.4 基于球的标定

2004年，Ying X H[5]通过几何不变量找到了基于球的两个不变量约束方程(方程(6)和方程(7))，运用三个球就可以非线性标定折反射相机。2008年，Ying X H等人[23]在2004年的几何不变量标定折反射相机的基础上，通过修改绝对二次曲线的像(MIAC),在像平面上得到一个与IAC同心的圆,运用双触点定理(Double-Contact Theorem)线性标定折反射相机。但是，以上两种方法对于抛物折反射方法是退化的。2012年，Duan H等人[8]解决了这种退化情形，步骤如下：首先在像平面上抛物镜面投影的轮廓线是可视的，用其轮廓线初始化内参数；提取k(k≥3)个视点下的两个球面像，运用初始化的内参数最小化目标方程:

(21)

(22)

得到两个平行圆C±i的表达式；求解C±i的公共解找到圆环点的像得出绝对二次曲线的像，从而标定相机。但是，此方法仅适用于抛物折反射相机。

3.5 自标定

自标定方法适用于多视图中点对应，无需知道空间点位置及相机位置。2000年，Kang S B[24]给出了抛物折反射摄像机的自标定方法，直接从场景图像出发，使用多幅图像对应点之间的约束最小化目标方程：

(23)

来标定抛物折反射像机。其中，Npairs为不同图像对的数量，med代表误差εij的中间值，该方法的优点在于不需要使用标定块就可以直接标定中心折反射相机。2002年，Svoboda T[3]扩展了透视相机的极几何到所有中心折反射相机上，得到三维空间中对应射线的几何性质，得到像点的约束方程，从而得到中心折反射相机所有镜面的极几何约束。2010年，Ramalingam S等人[25]考虑在没有任何平移和旋转参数的前提下，使用纯平移和纯旋转，从摄影射线的图像匹配得到几何约束来标定中心相机。2011年，Espuny F[26]提出了一个与Ramalingam S类似的方法，相机围绕着过投影中心线性无关的两条未知线旋轴旋转得到两个密集的旋转流，得到一个封闭形式的解，进而标定中心相机。

在此我们将本文中提及的近10年摄像机标定方法按时间分布如表2所示，并给出各方法之间的对比，如表3所示。

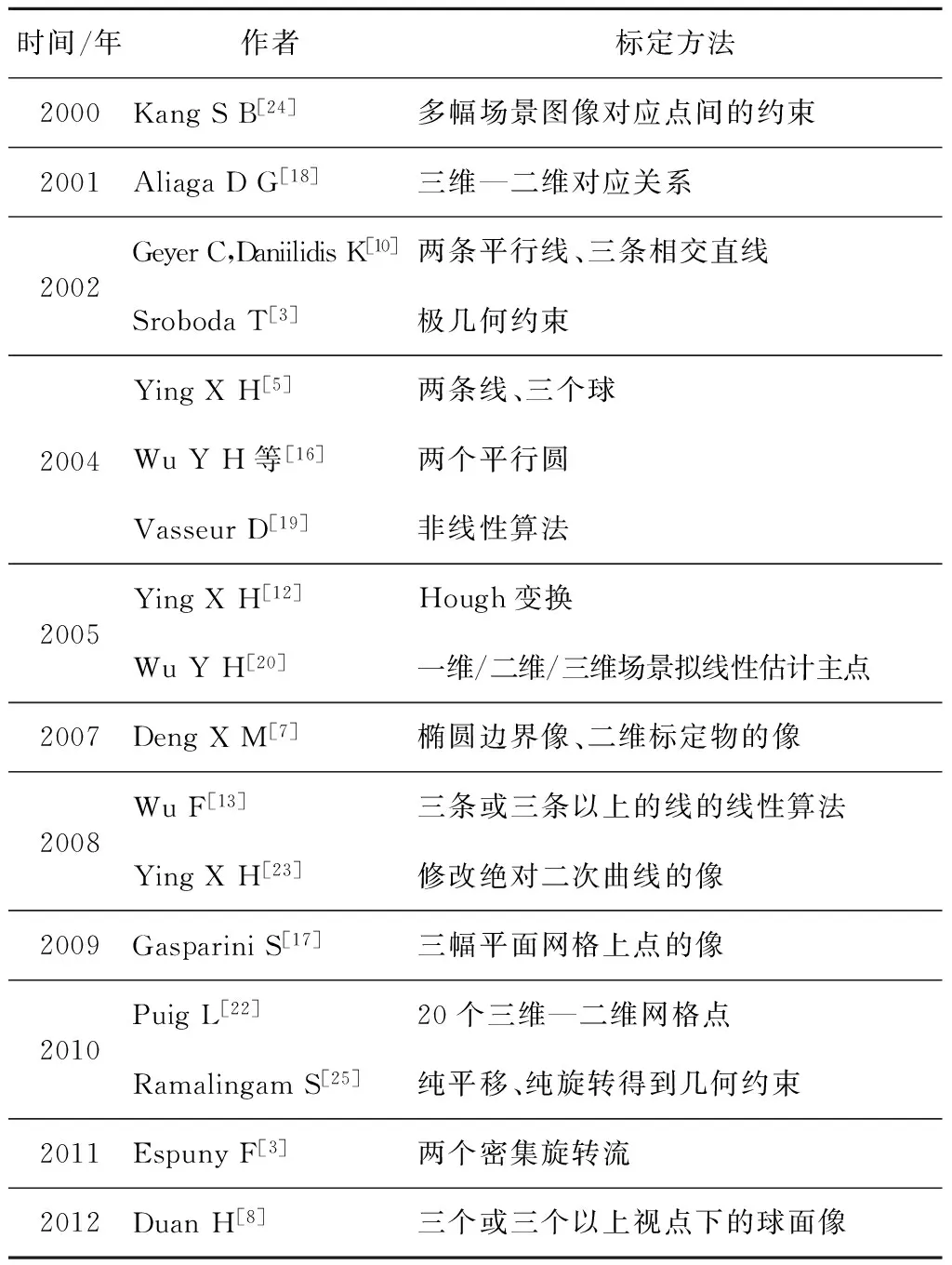
Table 2 Distribution table over the past decade

4 结束语

本文系统地论述了国内外10年来中心折反射相机的标定方法，将其分为五种方法，对其适用的范围以及优缺点做了简单的概括。对于中心折反射相机来说，由于其大视场的特点越来越受到研究者们的喜爱，随着算法的深入研究，标定精度越来越高，鲁棒性越来越强，适用范围越来越广。抛物折反射相机相对于双曲折反射相机和椭圆折反射相机来说，标定方法更加成熟而且比较全面。基于球面的折反射相机标定仍然是一个具有挑战性的开放性问题，暂时还没有找到一种算法可以适用于所有类型折反射相机。

Table 3 Comparison among

[1] Baker S, Nayer S. A theory of single-viewpoint catadioptric image formation[J]. International Journal of Computer Vision, 1999, 35(2):175-196.

[2] Geyer C, Daniilidis K. Catadioptric projective geometry [J]. International Journal of Computer Vision, 2001, 45(3):223-243.

[3] Svoboda T,Pajdla T.Epipolar geometry for central catadioptric cameras [J]. International Journal of Computer Vision, 2002, 49 (1):23-37.

[4] Geyer C, Daniilidis K. A unifying theory for central panoramic systems and practical applications[C]∥Proc of the 6th European Conference on Computer Vision Part II, 2000:445-461.

[5] Ying Xiang-hua, Hu Zhan-yi. Catadioptric camera calibration using geometric invariants[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 26 (10):1260-1271.

[6] Barreto J P,Araujo H.Issues on the geometry of central catadioptric image formation[C]∥Proc of IEEE Conference on Computer Vision and Pattern Recognition, 2001:422-427.

[7] Deng Xiao-ming, Wu Fu-chao, Wu Yi-hong. An easy calibration method for central catadioptric cameras[J]. Acta Automatic Sinica, 2007,33(8):801-808.

[8] Duan Hui-xian, Wu Yi-hong. A calibration method for paracatadioptric camera from sphere images[J]. Pattern Recognition Letters, 2012, 33(6):677-684.

[9] Puig L, Bermudez J, Sturm P, et al. Calibration of omnidirectional cameras in practice:A comparison of methods [J]. Computer Vision and Image Understanding, 2012,116(1):120-137.

[10] Geyer C, Daniilidis K. Paracatadioptric camera calibration[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(5):687-695.

[11] Barreto J P, Araujo H. Geometric properties of central catadioptric line images and their application in calibration[J]. Pattern Analysis and Machine Intelligence, 2005, 27(8):1327-1333.

[12] Ying Xiang-hua, Zha Hong-bin. Simultaneously calibrating catadioptric camera and detecting line features using Hough transformation[C]∥Proc of IEEE/RSJ International Conference on Intelligent Robots and Systems, 2005:1343-1348.

[13] Wu Fu-chao, Duan Fu-qing, Hu Zhan-yi, et al. A new linear algorithm for calibrating central catadioptric cameras [J]. Pattern Recognition, 2008,41(10):3166-3172.

[14] Barreto J P, Araujo H. Fitting conics to paracatadioptric projections of lines[J]. Computer Vision and Image Understanding, 2006, 101(3):151-165.

[15] Sturm P, Barreto J. General imaging geometry for central catadioptric cameras [C]∥Proc of European Conference on Computer Vision, 2008:609-622.

[16] Wu Yi-hong, Zhu Hai-jiang, Hu Zhan-yi, et al. Camera calibration from the quasi-affine invariance of two parallel circles[C]∥Proc of European Conference on Computer Vision, 2004:190-202.

[17] Gasparini S, Sturm P, Barreto J P. Plane-based calibration of central catadioptric cameras [C]∥Proc of International Conference on Computer Vision, 2009:1195-1202.

[18] Aliaga D G. Accurate catadioptric calibration for real-time pose estimation in room-size environments[C]∥Proc of the 8th International Conference on Computer Vision, 2001:127-134.

[19] Vasseur P, Mouaddib E. Central catadioptric line detection[C]∥Proc of British Machine Vision Conference, 2004:1.

[20] Wu Yi-hong, Hu Zhan-yi. Geometric invariants and applications under catadioptric camera model [C]∥Proc of International Conference on Computer Vision, 2005:1547-1554.

[21] Deng Xiao-ming, Wu Fu-chao, Duan Fu-qing, et al. Catadioptric camera calibration with one-dimensional objects[J]. Chinese Journal of Computers,2007,30(5):737-747.(in Chinese)

[22] Puig L,Bastanlar Y,Sturm P,et al.Calibration of central catadioptric cameras Using a DLT-Like approach[J]. International Journal of Computer Vision, 2011, 93(1):101-114.

[23] Ying Xiang-hua,Zha Hong-bin.Identical projective geometric properties of central catadioptric lines images and sphere images with applications to calibration[J]. International Journal of Computer Vision, 2008, 78(1):89-105.

[24] Kang S B. Catadioptric self-calibration [C]∥Proc of the IEEE Conference on Computer Vision and Patten Recognition, 2000:201-207.

[25] Ramalingam S, Sturm P, Lodha S K. Generic self-calibration of central cameras[J]. Computer Vision and Image Understanding, 2010, 114(2):210-219.

[26] Espuny F, Gil J B. Generic self-calibration of central cameras from two rotational flows[J]. International Journal of Computer Vision, 2011, 91(2):131-145.

附中文参考文献：

[21] 邓小明,吴福朝,段福庆,等,基于一维标定物的反射折射摄像机标定方法[J].计算机学报，2007,30(5):737-747.

ZHANGYan,born in 1986,MS candidate,her research interest includes the study of central catadioptric camera calibration.

赵丽娜(1974-),女,河北保定人，博士，副教授，研究方向为计算机视觉。E-mail:zhaoln@mail.buct.edu.cn

ZHAOLi-na,born in 1974,PhD,associate professor,her research interest includes computer vision.

胡万宝(1984-),男,河北张家口人,硕士，研究方向为人脸识别。E-mail:huwanbao2008@163.com

HUWan-bao,born in 1984,MS,his research interest includes face recognition.

Reviewofcentralcatadioptriccameracalibrationmethods

ZHANG Yan,ZHAO Li-na,HU Wan-bao

(College of Science,Beijing University of Chemical Technology,Beijing 100029,China)

In recent dozen years,computer vision becomes more popular,in which omnidirectional camera has a larger field of view (FOV) and widely been used in many fields,such as:robot navigation,visual surveillance,virtual reality, three-dimensional reconstruction, and so on.Camera calibration is an essential step to obtain three-dimensional geometric information from a two-dimensional image.Camera calibration results directly decide the results of 3-D reconstruction and other computer vision application effect.Hence,the study of such camera calibration method has important theoretical significance and practical applications.The paper classifies these methods from 2000 to 2012,by means of the difference calibration blocks,into five categories:calibration based on line;calibration based on two-dimensional calibration block;calibration based on three-dimensional point;calibration based on balls;self-calibration. And these methods’advantages and disadvantages are analyzed.

spherical model;catadioptric;camera calibration

1007-130X(2014)05-0951-06

2012-09-24;

：2013-03-12

国家自然科学基金天元基金资助项目(10926187)；中央高校基本科研业务费专项资金资助项目(ZZ1019)；国家自然科学青年基金资助项目(11301021)

TP391.4

：A

10.3969/j.issn.1007-130X.2014.05.028