气动喷射数值仿真分析

邵中青，张辽远,王 硕,吕忠秀

(沈阳理工大学 机械工程学院，辽宁 沈阳 110159)

气动喷射数值仿真分析

邵中青，张辽远,王 硕,吕忠秀

(沈阳理工大学 机械工程学院，辽宁 沈阳 110159)

利用CFD软件Fluent建立数学物理模型，运用欧拉法和拉格朗日方法相结合的计算模型对离散相模型(DPM)进行三维数值模拟。研究当进口处空气速度为60m/s时，不同直径的固体颗粒在喷管外部流场的轨迹和横截面上的分布。仿真得到以下结论：在固体颗粒从喷管喷出后短距离内，固体颗粒大体上呈现圆锥状喷射，喷射的锥角随颗粒的减小而逐步减小；颗粒直径减小时，长轴半径接近短轴半径，逐步过渡为圆形。

欧拉法和拉格朗日方法相结合；离散相模型；圆锥状喷射

固体粉末状或颗粒状物料可以借助气固喷射器输送装置进行方便快捷的运输，主要是通过气体在管道内高速流动的动能实现运输功能，其管道布置灵活，输送的物料不会被污染，与传统的带式、链式输送机输送相比，有不可比拟的优点，因而应用领域广泛[1]。许多国内外学者通过不懈研究，逐渐形成了一套成熟的气固喷射器结构和流动的理论。目前的气固喷射器主要有传统型喷射器和同心型气固喷射器，熊源泉等[2]也曾对传统气固喷射器进行了改进和创新。

目前国内外已有学者对两相流做了一些研究，主要有两种模型:一种是欧拉-拉格朗日模型,另一种是欧拉双流体模型[3]。其主要研究的是管道内部的流场分析，尤其集中在水射流的研究，且逐步趋于成熟，很少研究管道外部的流场分析，特别是对于固体颗粒在外部流场的喷射情况的研究更少。本文主要运用Fuent仿真软件研究从喷头喷出后管道外部固体颗粒的分布及轨迹，对气相场采用欧拉法，用k-ε双方程进行计算,对固相采用基于拉格朗日法的直接数值模拟法进行计算；对喷播设备进行探索与研究。

1 Fluent的理论依据

1.1 气相输送方程

(1)连续方程

式中：i、j=1、2、3，表示坐标方向，以下相同含义；ρ为流体密度;Uj为气体速度。

(2)动量方程

式中：

当φ≤0.8时，

当φ>0.8时，

式中：Re=ρφ|Y-U|dP/μ；ξ为颗粒的球形度；dP为颗粒直径；Re为雷诺数。

1.2 湍流动能方程和湍流动量耗散方程

(1)湍流动能方程(k方程)

由于颗粒对气相的湍流具有一定的影响，考虑到实际因素，选择文献[4]中提出的湍流动能方程:

(2)湍流动量耗散方程(ε方程)

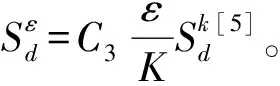
2 建立模型

建模时需满足：CPU为Inter(R) Celeron(R) E3200 双核；内存2GB，独立显卡，显存根据主板等的性能配置。为研究固体颗粒从喷管喷出后短距离(2m以内的)的自由喷射情况，建立半径为3m，长度为20m一个足够大的外部流域，满足自由喷射。整体结构是轴对称结构，采用三维单精度方法计算，建立三维轴对称计算模型，节省计算时间。二维模型如图1所示，三维空间模型如图2所示。

为研究方便，可通过建立对称平面(由于尺寸上相差较大，只是画出大体的示意图)，研究这一平面上的固体颗粒轨迹，从整体上模拟出固体颗粒的喷射状态。AI代表半径为36mm的平面，作为气体的入口，边界类型设置为Velocity-inlet；CD代表半径为36mm的平面，作为固体颗粒的入口，边界类型设置为Velocity-inlet；KL代表半径为3000mm的平面；JKLM为图中所示较大的圆柱面，作为气固混合物的出口，边界类型设置为Outflow。其余平面尺寸大小如表1所示。

表1 模型的尺寸大小 mm

图1 二维模型

图2 三维空间模型

3 Fluent下的仿真分析

本文对气相场采用欧拉法，用三维k-ε双方程进行计算；对固相采用基于拉格朗日法的直接数值模拟法。可假定所研究的空间区域内的气体温度维持稳定不变，且忽略固体颗粒与壁面间的相互作用。参照Simple算法，应用离散相模型(DPM)，对气固两相进行耦合求解。模型的计算条件见表2所示。

Simple算法计算步骤如下：首先假定一个速度分布，记为u0、v0、w0，以此计算动量离散方程中的系数及常数项；然后假设一个压力场p0，依次求解动量方程，得u1、v1、w1；再对压力加以修正，得p1，根据p1改进速度值；利用改进后的速度场求解通过源项物性等与速度场耦合的Φ变量，如果Φ变量不影响流场，则应在速度场收敛后再求解；最后利用改进后的速度场重新计算动量离散方程的系数，并利用改进后的压力场作为下一层次迭代计算的初值。重复上述步骤，直到收敛。仿真软件Fluent界面与Simple算法求解参数设置分别如图3、图4所示。

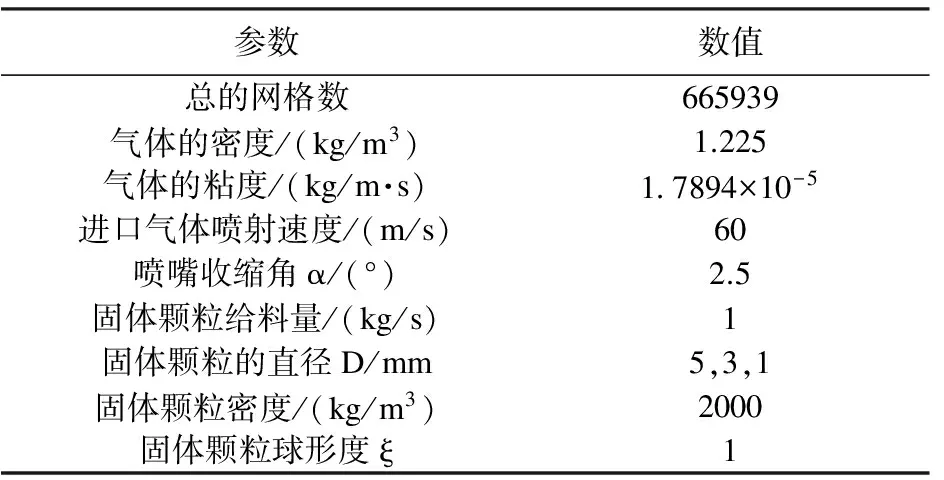
表2 本文模型计算条件

图3 仿真软件Fluent界面

图4 Fluent中Simple算法的设置

3.1 同一速度(60m/s)下不同大小的颗粒轨迹

轨迹图5～7分别是入口空气速度为60m/s，直径为5mm、3mm、1mm的固体颗粒在对称截面上的轨迹分布。可以看出固体颗粒全部喷出所需要时间t(s)分别为1.68、1.64、1.73，时间随着固体颗粒直径的增大先减小后增大。

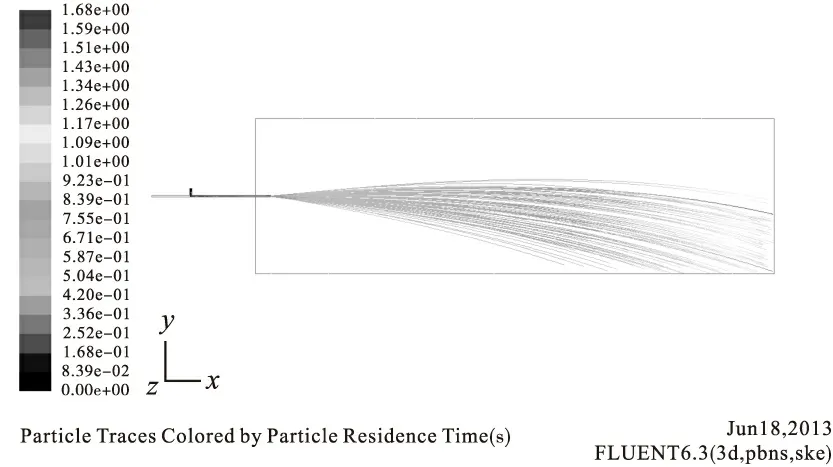
图5 直径D=5mm颗粒的轨迹

图6 直径D=3mm颗粒的轨迹

图7 直径D=1mm颗粒的轨迹

由图5～7可以看出，固体颗粒全部喷出所需时间t并不随颗粒的大小单调性的增减。固体颗粒较小或较大时，其运动的平均速度较小，全部喷出所需要的时间t较长；当固体颗粒大小适中时，其运动的平均速度较大，全部喷出所需要的时间t较短。主要原因是：能量的总损失主要包括两部分—克服重力所造成的能量损失和克服固体颗粒与壁面的摩擦所造成的能量损失。当固体颗粒的直径较大时，体积较大，重力相对较大，克服重力消耗的能量较多，能量损失较多，因而固体颗粒全部喷出所需要时间相对较长；当直径很小时，体积较小，重力相对较小，克服重力消耗的能量较小，但此时一些颗粒会悬浮甚至贴附在上壁面上，克服固体颗粒与壁面的摩擦所消耗的能量较多，使能量的总损失较多，固体颗粒全部喷出所需要的时间相对较大；当固体颗粒的直径适中时，体积刚好，重力适中，克服重力所消耗的能量相对于大颗粒少，同时贴附在上壁面上的固体颗粒数量相对于小颗粒较少，使得能量的总损减小很多，因此固体颗粒运动的平均速度较大，全部喷出所需时间较少。

3.2 同一速度(60m/s)下不同大小的颗粒在横截面上的分布

研究大小不同的三种固体颗粒从喷嘴喷出后距离喷嘴1000mm、2000mm的横截面上的分布情况，分布范围如图8～10所示(图像关于Z=0对称，所给图像只显示了Z<0的一部分)。其中D为颗粒直径，L为横截面距离喷嘴的距离。

图8 颗粒直径D=5mm的截面颗粒分布

图9 颗粒直径D=3mm的截面颗粒分布

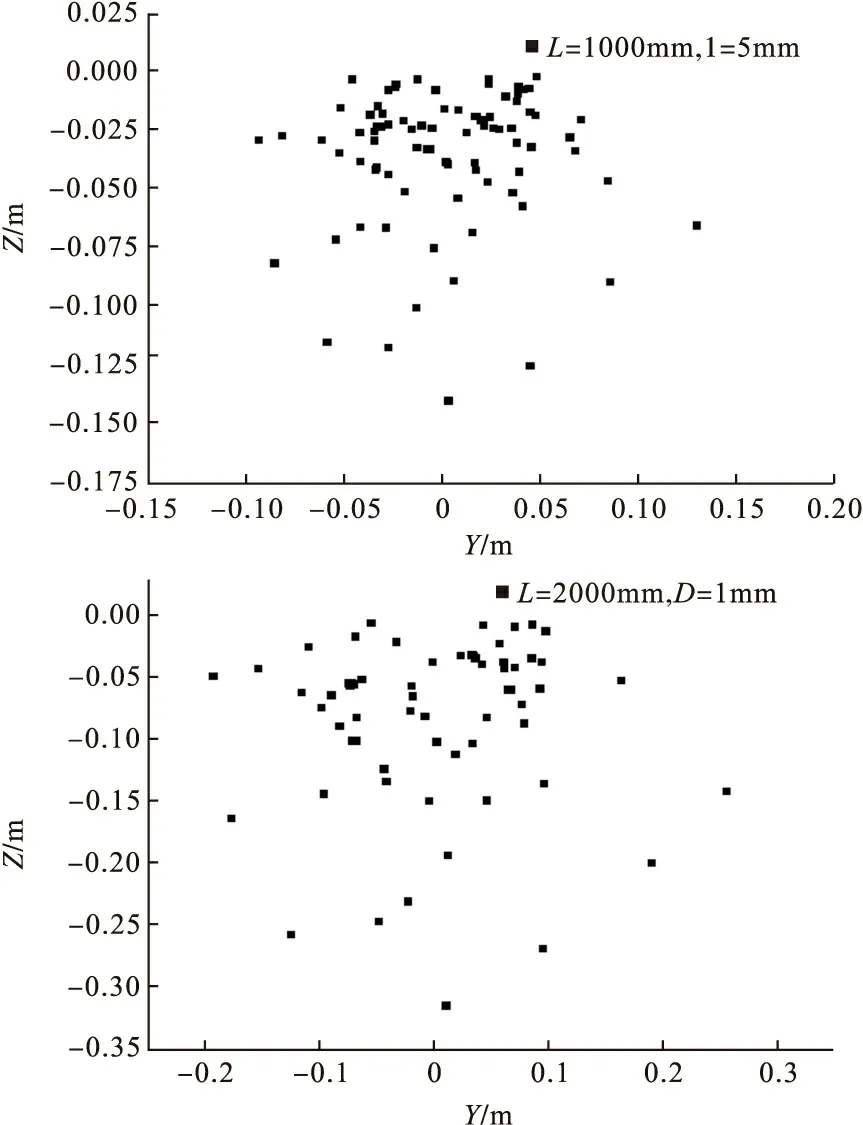
图10 颗粒直径D=1mm的截面颗粒分布

表3 横截面颗粒各向分布半径 mm

结合表3和图8～10，通过对比分析可以发现：颗粒的分布整体近似呈现出椭圆形，长轴沿Z方向，短轴沿Y方向；距离喷嘴的距离L值相同时，k1

此外，气动能量对颗粒喷射的影响可通过气体速度和颗粒质量流量反映出来。气体速度一定情况下，只考虑质量流量的影响。分别选取固体颗粒质量流量(kg/s)为0.5、1、3，颗粒半径(mm)为5、3、1进行研究。通过仿真分析可知，质量流量为1kg/s时的三种颗粒的分布半径大致为0.5kg/s时的2倍，但质量流量为3kg/s时的分布半径基本与0.5kg/s相同，且像1mm这样的小颗粒喷射效果较差；同时发现质量流量对喷射锥角的影响很小。随着颗粒质量流量的增加，颗粒分布半径先呈现线增长，之后减小。表明在一定范围内较大的质量流量有利于颗粒获得较大的喷射覆盖面积，但超出这个范围，反而会适得其反。二者的具体关系尚需进一步深入研究。

4 结论

(1)在固体颗粒从喷管喷出后短距离内，固体颗粒大体上呈现圆锥状喷射，喷射的锥角随固体颗粒的增大而增大。

(2)固体颗粒全部喷出所需时间并不随固体颗粒的大小单调性的增减，固体颗粒较小或较大时，所需时间相对较长，固体颗粒运动的平均速度较大；当固体颗粒大小适中时，所需时间较小，固体颗粒运动的平均速度较大。

(3)颗粒的分布整体近似呈现出椭圆形，当颗粒直径减小时，长轴半径接近短轴半径，逐步过渡为圆形；对直径相同的颗粒，颗粒分布的集中性随离喷嘴的距离的增大变得相对均匀；颗粒越大，其分布的范围就越大。

[1]卢孟龙，贾明生.直立螺旋——气固喷射器小型给粉装置[J].硫磷设计与粉体工程，2007，(2)：24-27.

[2]熊源泉，袁竹林，章名耀.加压条件下气固喷射器输送特性的三维数值模拟[J].化工学报，2004，55(10)：1638-1643.

[3]鲍仲辅,杜群贵,谢恺.基于欧拉双流体模型对气固喷射器三维数值仿真[J].流体机械，2010，38(5)：24-28.

[4]Crowe C T.On models for turbulence modulation in fluid-particle flows[J].Int，J，Multiphase Flow，2000，26(5)：719-727.

[5]Bertodano M L，Lahey R T，Jones O C.Development of a K-ε model for bubbly two-phase flow[J].Trans，of the ASME，J.Fluids Eng，1994，116(1)：128-134.

[7]Elghobashi S E，Abou-Arab T W.A two-equation turbulence model for two-phase flows[J].Phys Fluids，1983，26(4)：931-938.

PneumaticJetNumericalSimulation

SHAO Zhongqing,ZHANG Liaoyuan,WANG Shuo,LV Zhongxiu

(Shenyang Ligong University,Shenyang 110159,China)

The simulation idea of CFD software Fluent was adopted,and the mathematical physical model was established,and by the calculation model combining Euler method and Lagrange method,three-dimensional numerical simulation was applied to discrete phase model (DPM).Different diameter of solid particles on the outside of the nozzle flow field on the particle trajectories and the distribution of solid particles on cross section mainly were studied,under the circumstance of the inlet air speed of 60 m/s.Through the simulation the following conclusion was got:within short distance after solid particles ejected from nozzle,solid particles generally presented the conical spray,spray cone angle increased gradually with the reduction of particle diameter decreasing;with the particle diameter decreasing,long axis radius is closer to the short axis radius,gradually transforming to the circular.

combining Euler method and Lagrange method;discrete phase model;conical spray

2013-07-10

邵中青(1986—)，男，硕士研究生；通讯作者：张辽远(1962—)，男，教授，博士，研究方向：精密及特种加工.

1003-1251(2014)01-0081-06

O355

A

赵丽琴)