基于人工生命种群的人工生态系统演变研究*
2014-09-13冯康
冯 康
(淮南师范学院计算机与信息工程系,安徽 淮南 232038)
基于人工生命种群的人工生态系统演变研究*
冯 康
(淮南师范学院计算机与信息工程系,安徽 淮南 232038)
运用人工生命技术探索生态系统演变的规律,提出了人工生命种群的当量模型;建立了一个基于人工生命种群的人工生态系统,从底层到最顶层依次为模拟气候、人工生态环境、人工植物种群、食草人工动物种群、食肉人工动物种群。开展了人工生态系统演变实验。实验发现,平衡态人工生态系统存在收窄现象,但从不越界,只要模拟气候不低于其临界值,人工生态系统就将继续处于平衡态;但任一生态层在某时刻起低于其临界值将使人工生态系统从该时刻起处于失衡态,失衡态是不可逆的,除非外界足量补缺。基于人工生命种群的人工生态系统演变研究弥补了现有生态系统演变研究存在的缺陷,研究结果揭示了生态系统演变的规律,因此它是研究生态系统演变的科学方法。
人工生命种群;人工生态系统;临界值;平衡态;失衡态
1 引言
生态系统演变研究的目的是建立能够准确描述生态系统演变的通用算法模型,并利用计算、分析的方法,发现生态系统演变的一般规律[1]。为此,人们已经建立了多个描述某个具体生态系统演变的算法模型。Logistic模型是第一种考虑到种群的增长受制于环境的生态系统演变算法模型,但种群却是单一的[2]。Lotka-Volterra模型是一个描述两个种群间捕食-被捕食、竞争、互惠三种相互作用关系的生态系统演变算法模型,却忽略了环境的影响[3]。三种群的Lotka-Volterra模型可以体现生态系统中不同种群的食物链关系,并且可以扩展为n种群的Lotka-Volterra模型,但它们没有考虑种群不同时期的状态对相互作用的影响,即时滞[4]。具时滞的Hastings模型充分考虑到两个种群个体在幼年、成年时期对相互作用的影响,反映了生态系统的未来不但与生态系统的现在有关,还与生态系统的过去状态有关,但没有考虑到近年来急剧污染的环境对种群的影响[5]。Gallopin污染模型描述了单一种群在污染环境中的数量变化规律,揭示环境污染可以导致种群的灭绝[6,7]。单一种群的可开发模型认为只要种群的初始数量足够大,且捕捞率合适,则种群的数量将稳定在一个可再生的值,不会灭绝[8]。
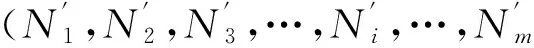
人工生命是具有自然生命系统行为特征的人造系统[11],是近年来利用计算机科学技术研究生命系统的有效手段,并产生了如CAM-Brain[12]、L-系统[13]、ALIFE[14]、“晓媛的鱼”[15]、原核细胞能量代谢模型E-CELL[16]等应用于生产实践的研究成果。人工生命种群作为一个群体级的人工生命,有着和自然生物种群相似的演变规则,并以自身特有的方式和周围环境及其它人工生命种群发生相互作用,因此非常适合描述自然生态系统中的生物种群[17]。
2 人工生命种群的当量模型
2.1 人工生命种群的当量
2.1.1 当量表示法
人工生命种群ALP(Artificial Life Population)是在某一时刻t占据某一人工生态环境中的所有同种人工生命个体的集合。完整地描述一个人工生命种群应该包括该时刻种群内所有个体的全部属性值,既有数量、质量、性别(雌雄),还有繁殖能力、生命力、能量储备、健康状况等属性的量化表达[18]。为简化描述,可对该时刻所有的个体的全部属性进行加权求和,得到人工生命种群的当量y(t),并用当量来表达该人工生命种群。
定义1(人工生命种群的当量)。令t时刻人工生命种群中某个个体ai=ai1,ai2,…,aip,其中ai1,ai2,…,aip为个体ai的p个属性的量化表达,种群内个体的数量为n,则该时刻人工生命种群的当量y(t)可表示为:
其中,k1, k2,…, kp为ai1, ai2,…, aip对应的权值,是一组常量。由于每个个体的属性ai1, ai2,…, aip及种群中个体的数量n均随着时间t的延续在改变,因此人工生命种群的当量y(t)在时刻改变着。
2.1.2 平衡与失衡
生物学的研究已经证明,每种自然生物种群都有一个对应的种群规模最小值Smin,若种群的规模低于该值,则该种群在有限的时间内必然不可逆地走向灭绝;反之,种群则能保持平衡或发展[19]。参照自然生物种群的种群规模最小值Smin,我们定义人工生命种群的灭绝当量。
定义2(灭绝当量)。若t时刻某人工生命种群的当量y(t)
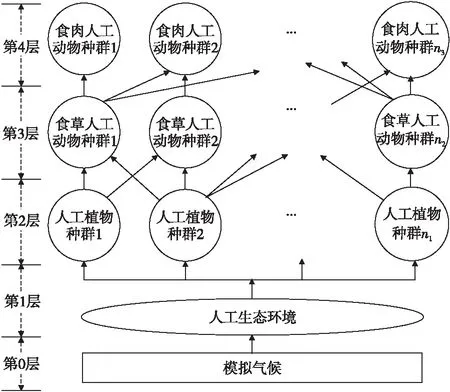
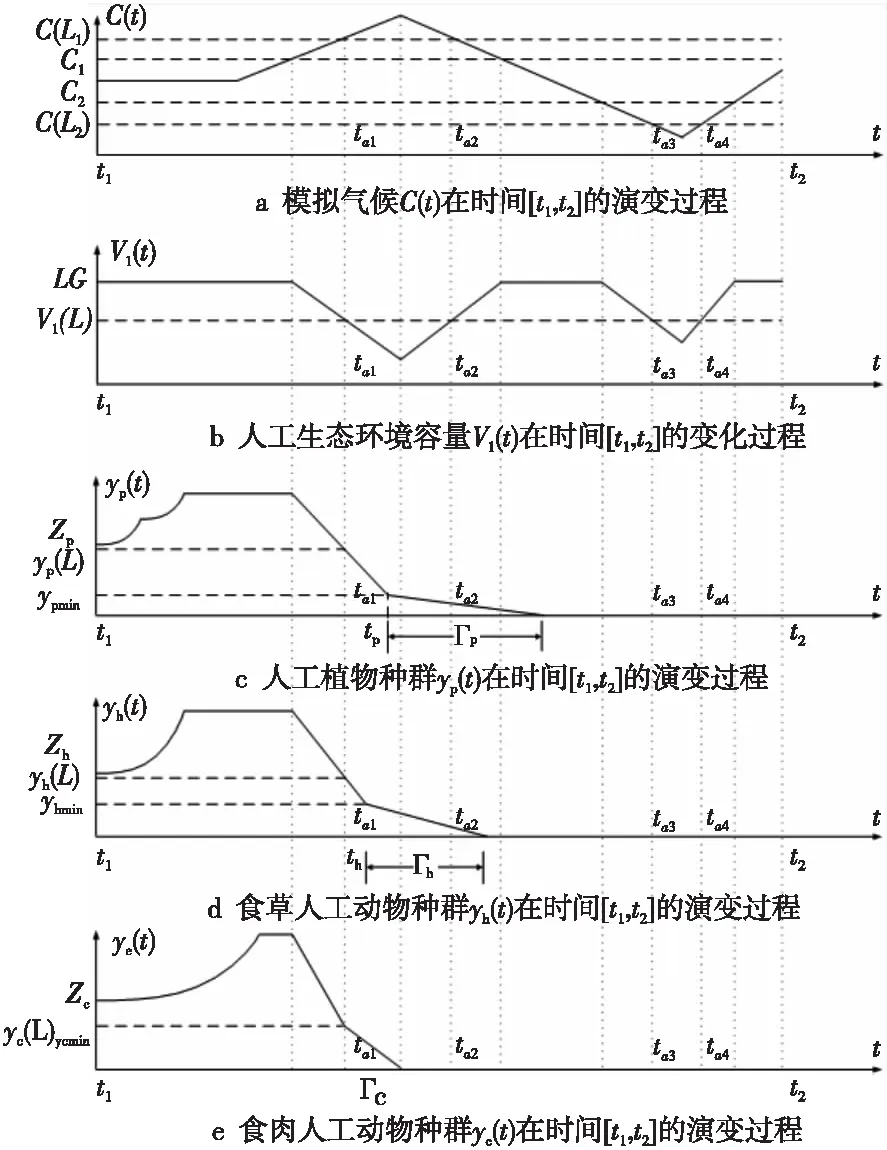
若在一个有限的时间区间[ti,tj]内,人工生命种群的当量均大于或等于其灭绝当量,即t∈[ti,tj], 且y(t)≥ymin,则称该人工生命种群在时间区间[ti,tj]内保持平衡;反之,若在tp时刻y(tp)=ymin,但此后y(t) 2.2 消费-生产系统 任何一个人工生命种群y(t)在某一时刻t都是一个消费-生产系统。首先人工生命种群都需要消费供应方提供一定量的营养物质x(t),并产生一定当量的人工生命种群y(t)提供给该人工生命种群之外作为产品,二者之间遵循特定的消费-生产方式f()。因此,人工生命种群y(t)可以表示为一个消费-生产系统,即y(t)=f(x(t))。 大量的统计数据表明,生态系统中,在营养物质x(t)被生物种群完全消费时,生物种群的消费-生产方式f()近似为线性关系[20]。因此,人工生命种群y(t)可以模拟为: (1) 其中,0 特别地,若y(t)=ymin,根据式(1),x(t)=ymin/Q,并称该值为人工生命种群的营养物质底,记作xmin,显然,xmin=ymin/Q,是一个与种群密切相关的常量。 2.3 演变系统 任何一个人工生命种群都是一个演变系统。假设某人工生命种群在t=0时刻的初始当量为Z(Z≥ymin),且外界提供的营养物质始终不低于人工生命种群需要消费的营养物质x(t),则随着时间t的延续,人工生命种群在Z的基础上,依靠消费营养物质x(t),按照人工生命种群自身的演变规律g(t)在发生演变。因此,人工生命种群y(t)可以表示为: (2) 其中,g(t)是该人工生命种群的演变规律。根据已有的统计数据,生态系统中属于不同纲目的生物种群的演变规律差异较大[21]。因此,参照生态系统中生物种群的演变规律可知,人工植物种群、食草人工动物种群及食肉人工动物种群的演变规律是不同的。 2.4 人工生命种群的当量模型 由于人工生命种群既是一个消费-生产系统,又是一个演变系统,因而二者是统一的,根据式(1)和式(2),可得Qx(t)=Zg(t),即x(t)=Z/Qg(t)。因此,人工生命种群消费的营养物质x(t)随着人工生命种群的演变在时刻变化,而人工生命种群消费的营养物质x(t)来源于供应方,假设供应方能够给人工生命种群提供的营养物质总量为xs(t),根据式(1)和式(2),并考虑到人工生命种群的平衡与失衡,则人工生命种群的一般模型可用下式表达: (3) 由于式(3)表达的人工生命种群一般模型是以当量来表达人工生命种群的变化,因此式(3)表达的人工生命种群一般模型又称人工生命种群的当量模型。 典型生态系统的构成不但包括构成食物链的生物种群,而且还包括生物种群生长的生态环境及影响生态环境的气候。在这样的生态系统中,有处于食物链最顶层的食肉动物种群(如狼群)、处于食物链中间层的食草动物种群(如驯鹿群)、处于食物链最底层的植物种群(如森林、牧草),还有位于食物链下层的整个食物链种群赖以生长的生态环境,而气候的变化直接影响着生态环境,因此气候构成了整个生态系统的最底层。仿真典型生态系统的构成,我们建立一个基于人工生命种群的人工生态系统。 3.1 基于人工生命种群的人工生态系统结构 人工生态系统AE(ArtificialEcosystem)是基于人工生命种群的模拟生态系统,它由五个生态层构成,从底层到最顶层依次是模拟气候(第0层)、人工生态环境(第1层)、人工植物种群(第2层,由n1个人工植物种群组成)、食草人工动物种群(第3层,由n2个食草人工动物种群组成)和食肉人工动物种群(第4层,由n3个食肉人工动物种群组成),这些生态层之间相互作用的关系如图1所示。其中,模拟气候位于人工生态系统的最底层(第0层),它的变化影响着位于第1层的人工生态环境;人工生态环境为第2层的n1个人工植物种群提供营养物质,人工植物种群为第3层的n2个食草人工动物种群提供营养物质,食草人工动物种群为最顶层的n3个食肉人工动物种群提供营养物质。我们把经由模拟气候→人工生态环境→一个人工植物种群→一个食草人工动物种群→一个食肉人工动物种群的相互作用关系传递链条称为一条生态链,这样,在图1所示的人工生态系统中最多可能存在n1×n2×n3条生态链。为讨论的方便,本文只研究含有一条生态链的人工生态系统,即单链人工生态系统。 Figure 1 Structure of the artificial ecosystem based on artificial life population图1 基于人工生命种群的人工生态系统结构 在人工生态系统中,除了最底层的模拟气候及处于最顶层的食肉人工动物种群外,其它处于不同层次的生态层都在为其上面的生态层提供营养物质,成为其上面生态层的营养物质供应方,即人工生态环境为人工植物种群的营养物质供应方,人工植物种群为食草人工动物种群的营养物质供应方,食草人工动物种群为食肉人工动物种群的营养物质供应方。我们把时刻t某个生态层能够为其上层提供的营养物质总量称为该生态层的容量V(t),并将人工生态环境、人工植物种群、食草人工动物种群对应的容量分别记作V1(t)、V2(t)、V3(t)。 3.2 模拟气候C(t) 自然界某个地区的气候是个复杂的时变系统,与大气环流、洋流、太阳辐射、纬度、海拔等变量及常量密切相关。大量的气候研究结果表明,在一个有限的时段内,自然界的气候是以某种相同的趋势在线性变化,但在不同的时段内,气候的变化趋势是不同的[22]。如冰河期全球气候逐渐变冷,间冰期全球气候逐渐变暖。根据CRU05资料的研究结果显示,在1901~2000年的100年间,中国气候共经历了变冷、变暖、变冷、变暖四次不同的变化年代际,但每次变化持续的时间并不相同[23]。因此,模拟自然界气候的变化,可将时间按模拟气候的变化趋势划分为不同的时段,令第q时段的起始时刻为tq,该时刻的模拟气候量为C(tq),该时段的末尾时刻为tq+1,则位于第q时段t时刻人工生态系统的模拟气候量可以表示为: (4) 其中,Kq是第q时段模拟气候的变化率,若Kq=0,则可以认为模拟气候总体保持恒定;若Kq>0,则认为模拟气候以某种趋势在发生变化,如变暖;若Kq<0,则认为模拟气候以另一种相反的趋势在发生变化,如变冷。 3.3 人工生态环境 人工生态环境是人工生态系统中的模拟气候C(t)对某个面积为G的地域的影响结果,并产生光照、温度、降水量、土壤组成等输出量。这些输出量的联合作用构成了该地域的人工生态环境,其作用效果就是为生长在该地域的人工植物种群提供营养物质量的多少,即人工生态环境的容量,因此人工生态环境可以用人工生态环境的容量V1(t)来表达。大量的研究发现,当气候量处于某个区间[C1,C2]时,自然生态环境的容量基本恒定,只与该生态环境的地域面积G有关;当气候量越过这个区间,无论是增加还是减小,生态环境的容量都线性减小。其中,C1和C2均为统计气候量数据[24]。因此,人工生态环境的容量V1(t)可模拟为: (5) 其中,L是一个统计出的该人工生态环境地域的容量常量,G是该人工生态环境地域的面积,M是一个统计出的该人工生态环境地域的容量与气候变化的关系常量。可见,影响人工生态环境容量的决定因素是面积及气候,当面积一定时,气候处于最适宜气候区间时,人工生态环境的容量最大,其余气候条件下人工生态环境的容量都将减小。 3.4 人工植物种群模型 由人工生态系统的组成可知,人工植物种群消费的营养物质的供应方为人工生态环境,而人工生态环境能够给人工植物种群提供的营养物质总量xs(t)就是人工生态环境的容量V1(t)。因此,假设人工植物种群初始当量为Zp,效率为Qp(Qp<1),人工植物种群需要消费的营养物质为xp(t),营养物质底为xpmin,根据式(3),人工植物种群的模型可表达为: (6) 人工植物种群为采食人工植物的食草人工动物提供营养物质,人工植物种群能够为食草人工动物提供的营养物质总量与人工植物种群的当量成正比。因此,人工植物种群的容量可表示为: (7) 其中,Rp称为人工植物种群的能量转换系数,是一个与种群有关的常量,且Rp<1。 3.5 食草人工动物种群 已知生活在人工生态环境G中的食草人工动物种群不迁徙,其效率为Qh(Qh<1) ,初始当量为Zh,食草人工动物种群的营养物质底为xhmin,外界提供的营养物质总量xs(t)就是人工植物种群的容量V2(t),根据式(3),食草人工动物种群的模型可表示为: (8) 食草人工动物种群为食肉人工动物种群提供营养物质,它能为食肉人工动物种群提供的营养物质总量与食草人工植物种群的当量成正比,因此食草人工动物种群的容量可以表达为: (9) 其中,Rh称为食草人工动物种群的能量转换系数,是一个与种群有关的常量,Rh 3.6 食肉人工动物种群 由于人工生态系统中的食肉人工动物种群不迁徙,其效率为Qc(Qc<1),初始当量为Zc,食肉人工动物种群的营养物质底为xcmin,外界提供的营养物质总量xs(t)即是食草人工动物种群的容量V3(t),根据式(3),食肉人工动物种群的模型可表示为: (10) 食肉人工动物种群位于人工生态系统的最顶层,它的演变表示整个人工生态系统演变的最终结果。 定义3(平衡态人工生态系统)。若在一个有限的时间[ti,tj],人工生态系统AE的所有人工生命种群都保持平衡,即y(t)≥ymin,则称该时间区间内,人工生态系统处于平衡态,或称为平衡态人工生态系统,记作AE(t)=1,其中,t∈[ti,tj]。 4.1 平衡态人工生态系统的临界值 人工生态系统中,食肉人工动物种群位于人工生态系统的最顶层,其当量变化的最小值称为其临界值,记作yc(L);显然,yc(L)=ycmin。在某个时间区间内,为使人工生态系统处于平衡态,由食肉人工动物种群的临界值向下逐层递推求出各个生态层对应的最小值,该最小值称为对应生态层的临界值,记作y(L),人工生态系统全部生态层的临界值构成了平衡态人工生态系统的临界值,记作AE(L)。 若yc(L)=ycmin,则食肉人工动物种群的营养物质底为xcmin=ycmin/Qc;作为食肉动物种群营养物质的供应方,食草人工动物种群除了自身保持平衡外,还要保证食肉人工动物种群保持平衡,因此食草人工动物种群的容量V3(t)≥xcmin,即V3(t)≥ycmin/Qc,按照(9)式,则yh(t)≥ycmin/(QcRh),即食草人工动物种群当量变化的临界点是yh(L)=ycmin/(QcRh),显然,yh(L)≥yhmin;同样,根据式(7)和式(8),作为食草人工动物种群营养物质的供应方,人工植物种群当量变化的临界点是yp(L)=ycmin/(QcQhRhRp),yp(L)≥ypmin;类似地,根据式(6),作为人工植物种群营养物质的供应方,人工生态环境变化的临界点是V1(L)=ycmin/(QcQhQpRhRp),且V1(L)≤LG;再根据式(5),可得人工生态系统的最底层模拟气候的临界值有两个,分别是C(L1)=(C1+C2)/2+(LG/M-ycmin/(QcQhQpRhRp))及C(L2)=(C1+C2)/2-(LG/M-ycmin/(QcQhQpRhRp))。由于模拟气候生态层的临界值有两个,我们将这两个临界值联立记作C(L)=C(L2)∞C(L1),并将C(t) 4.2 平衡态人工生态系统的极大值 人工生态系统中,模拟气候位于人工生态系统的最底层,按照式(5),当其变化处于最佳气候[C1,C2],人工生态环境的容量最大,因此,称最佳气候[C1,C2]为模拟气候的极大值,记作C(M)=[C1, C2],显然,C(M)≥C(L);如果模拟气候量C(t)∈[C1,C2],记作C(t)=C(M),如果模拟气候量C(t) 由于C(M)=[C1, C2],根据式(5),则人工生态环境生态层的极大值V1(M)=LG;根据式(6),人工植物种群生态层的极大值yp(M)=QpLG;再根据式(7)、式(8),得出食草人工动物种群生态层的极大值yh(M)=RpQpQhLG;最后根据式(9)、式(10),得出食肉人工动物种群生态层的极大值yc(M)=RpQpRhQhQcLG。显然AE(M)=[ C(M), V1(M), yp(M), yh(M), yc(M)]。 4.3 平衡态人工生态系统演变研究 为研究人工生态系统的演变,在计算机上模拟了一个人工生态系统AE,并开展了多个AE在[ti,tj]处于平衡态的演变实验。其中,AE为一个单链人工生态系统,且AE(ti)=1。实验中,通过模拟气候C(t)的变化,沿着生态链,逐层递推上一生态层的演变,直至食肉人工动物种群生态层结束,得到该次实验人工生态系统的演变结果。汇总并分析全部实验的结果,取得平衡态人工生态系统的演变规律。 4.3.1 演变实验 图2展示了一个平衡态人工生态系统的演变实验,其中的各个子图即是平衡态人工生态系统AE在[t1,t9]从底层到最顶层演变的详细过程。 图2a所示的是模拟气候C(t)在[t1,t9]的演变过程。可见,C(L)=C(L2)∞C(L1),C(M)= [C1, C2],在[t1,t9],C(t)≥C(L)。图2a中,C(t)随着时间的延续,在八个不同的时段[t1,t2)、[t2,t3)、[t3,t4)、[t4,t5)、[t5,t6)、[t6,t7)、[t7,t8)、[t8,t9),按照八种不同的趋势在发生变化,其中,K1=0,K2<0,K3>0,K4=0,K5<0,K6>0,K7<0,K8>0。在(tc1,tc2),(tc3,tc4),(tc5,t9)时段,C(t)≠C(M),但仍然有C(t)≥C(L);而在其它时段,C(t)=C(M)。假设起始时刻t1时的模拟气候量为C(t1),按照式(4),则C(t)的全部变化情况归纳如下: 若该人工生态系统中人工生态环境的地域面积为G,该人工生态环境地域的容量常量为L,容量与气候变化的关系常量为M,则对应图2a演变的模拟气候量C(t)、人工生态环境的容量V1(t)将按式(5)发生演变,具体表达为: 可见,在C(t)=C(M)的时段,V1(t)=LG,即V1(t)= V1(M),而在C(t)≠C(M)的时段,V1(t)都在线性减小,但仍然存在V1(t) ≥V1(L)。对应图2a的[t1,t9],人工生态环境的容量V1(t)随时间演变的过程如图2b所示。 人工生态环境容量V1(t)的演变影响着生长在该环境中的人工植物种群当量的变化。对比图2b及图2c,在[t1,tv1]、[t3,tv2]、[t5,tv3]时段,人工生态环境容量V1(t)大于或等于人工植物种群所需的营养物质xp(t);而在其它时段,人工生态环境容量V1(t)都小于人工植物种群所需的营养物质xp(t),但仍然大于或等于人工植物种群的营养物质底xhmin。因此,人工植物种群按照式(6)的规律进行演变,具体情况如下: 根据式(7),对应图2c所示的人工植物种群的演变,人工植物种群容量V2(t)的变化如图2d所示。 人工植物种群容量V2(t)的变化影响着食草人工动物种群当量的变化,对应图2d,在[t1,th1]、[t3,th2]、[t5,th3]时段,人工植物种群容量V2(t)大于或等于食草人工动物种群所需的营养物质xh(t);而在其它时段,人工植物种群容量V2(t)都小于食草人工动物种群所需的营养物质xh(t)。因此,食草人工动物种群按照式(8)的规律进行演变,具体情况如下: 因此,对应着图2d人工植物种群容量V2(t)的变化,食草人工动物种群yh(t)的演变如图2e所示。可见,由于ah 类似地,食草人工动物种群的容量V3(t)的变化影响着食肉人工动物种群yc(t)的变化,在[t1,tr1]、[t3,tr2]、[t5,tr3]时段,食草人工动物种群容量V3(t)大于或等于食肉人工动物种群所需的营养物质xc(t);而在其它时段,食草人工动物种群容量V3(t)都小于食肉人工动物种群所需的营养物质xc(t)。因此,食肉人工动物种群按照式(10)的规律进行演变,具体情况如下: 因此,对应图2f所示食草人工动物种群容量V3(t)的变化,食肉人工动物种群yc(t)的演变如图2g所示。可见,由于ac 通过该实验可见,当AE(t1)=1时,对应模拟气候在[t1,t9]保持C(t)≥C(L)的演变,AE包含的一个人工植物种群gp(t)、一个食草人工动物种群gh(t)、一个食肉人工动物种群gc(t)在[t1,t9]均保持平衡,因此在[t1,t9],AE(t)=1。 4.3.2 实验总结 继续在计算机上进行AE的演变实验,保持模拟气候在[ti,tj],C(t)≥C(L)及AE(ti)=1的特征,逐一改变人工生态系统各个生态层的初值,得出的实验结果是一致的,即在[ti,tj],AE(t)=1。因此,我们可以得出平衡态人工生态系统演变的以下结论。 定理1(平衡态定理)若AE(ti)=1, 且在[ti,tj]总能保持C(t)≥C(L),则AE(t)=1,其中,t∈[ti,tj]。 证明(1)由于AE(ti)=1,故yc(ti) ≥yc(L),yh(ti) ≥yh(L),yp(ti) ≥yp(L),而yc(L)=ycmin,yh(L)≥yhmin,yp(L)≥ypmin,故yc(ti)=ycmin,yh(ti)≥yhmin,yp(ti)≥ypmin。 (2)因为C(t)=C(L),t∈[ti,tj],则若C(L1)=(C1+C2)/2+(LG/M-ycmin/(QcQhQpRhRp)),根据式(5),V1(t)=ycmin/(QcQhQpRhRp),即V1(t)=V1(L);若C(L2)=(C1+C2)/2-(LG/M-ycmin/(QcQhQpRhRp)),根据式(5),V1(t)=ycmin/QcQhQpRhRp),即同样V1(t)= V1(L);由于V1(t)=ycmin/(QcQhQpRhRp),根据式(6),则yp(t)=ycmin/(QcQhRhRp),即yp(t)=yp(L);由于yp(t)=ycmin/(QcQhRhRp),根据式(7)及式(8),yh(t)=ycmin/(QcRh),即yh(t)=yh(L);由于yh(t)=ycmin/(QcRh),根据式(9)及式(10),若yc(t)=ycmin,即yc(t)= yc(L)。因此,若C(t)=C(L),t∈[ti,tj],且yc(L)=ycmin,yh(L)≥yhmin,yp(L)≥ypmin,故yc(t)=ycmin,yh(t) ≥yhmin,yp(t) ≥ypmin。 (3)因为C(t)>C(L),t∈[ti,tj];即(C1+C2)/2+(LG/M-ycmin/(QcQhQpRhRp))>C(t)>(C1+C2)/2-(LG/M-ycmin/(QcQhQpRhRp)),根据式(5),V1(t)>ycmin/(QcQhQpRhRp),即V1(t)>V1(L);由于V1(t)>ycmin/(QcQhQpRhRp),根据式(6),则yp(t)>ycmin/(QcQhRhRp),即yp(t)>yp(L);由于yp(t)>(ycmin/QcQhRhRp),根据式(7)及式(8),yh(t)>ycmin/(QcRh),即yh(t)>yh(L);由于yh(t)>ycmin/(QcRh),根据式(9)及式(10),若yc(t)>ycmin,即yc(t)> yc(L)。因此,若C(t)>C(L),t∈[ti,tj],且yc(L)=ycmin,yh(L)≥yhmin,yp(L)≥ypmin,故yc(t)>ycmin,yh(t)>yhmin,yp(t)>ypmin。 综合上述三步,若AE(ti)=1, 且在[ti,tj]总能保持C(t)≥C(L),则yc(t)≥ycmin,yh(t) ≥yhmin,yp(t) ≥ypmin,因此,AE(t)=1,其中,t∈[ti,tj]。 □ 定理1说明,对于处于平衡态的人工生态系统,模拟气候的变化不低于其临界值是保证人工生态系统继续保持平衡的决定条件。 定理2(不越界定理)若人工生态系统AE在[ti,tj]时间区间内保持平衡,即AE(t)=1,其中,t∈[ti,tj],则人工生态系统从不越界,即存在AE(M)≥AE(t)≥AE(L)。 证明(1)由于对于t∈[ti,tj],AE(t)=1,所以min(yc(t))=yc(L);而若yc(t)=yc(L),则yh(t)=yh(L),即min(yh(t))=yc(L);依此类推,min(yp(t))=yp(L),min(V1(t))= V1(L),min(C(t))=C(L);而AE(L)=[yc(L), yh(L), yp(L), V1(L), C(L)]。因此AE(t)≥AE(L)。 (2)由于对于t∈[ti,tj],AE(t)=1,所以max(C(t))=C(M);而若C(t)=C(M),则V1(t)=V1(M),即max(V1(t))= V1(M);依此类推,max(yp(t))=yp(M),max(yh(t))=yh(M),max( yc(t))=yc(M);而AE(M)=[C(M),V1(M),yp(M),yh(M), yc(M)]。因此,AE(M)≥AE(t)。 综合上述两步,可得若AE(t)=1,则存在AE(M)≥AE(t)≥AE(L),其中,t∈[ti,tj]。 □ 定理2说明,平衡态人工生态系统的变化范围为临界值和极大值之间,且包括临界值和极大值本身。 定理3(收窄定理)对于AE(t)=1,t∈[ti,tj],且AE(ti)≠AE(M)。若在[tb0,tq0]时段存在C(t)=C(M),在[tb1,tq1]时段存在V1(t)=V1(M),在[tb2,tq2]时段存在yp(t)=yp(M),在[tb3,tq3]时段存在yh(t)=yh(M),在[tb4,tq4]时段存在yc(t)=yc(M),则必存在ti 证明由于AE(ti)≠AE(M),而在[tb0,tq0]时段存在C(t)=C(M),在[tb4,tq4]时段存在yc(t)=yc(M),且t∈[ti,tj],所以,ti □ 定理3说明,在处于平衡态的人工生态系统中,各个生态层开始出现极大值的时刻从底层到最顶层逐渐推迟,但结束时刻一致,从而造成各个生态层处于极大值的时长由底层到最顶层逐渐收窄,这种现象又称收窄现象。 定义4(失衡态人工生态系统)若从t=ta时刻起,人工生态系统的最顶层食肉人工动物种群开始失衡,即yc(ta)=ycmin,但此后yc(t) 5.1 失衡态人工生态系统演变的研究 继续开展人工生态系统演变的实验,模拟了多个AE中的生态层从t=ta时刻起开始失衡的演变案例,实验中,AE(ta)=1,此后依次使AE中的模拟气候、人工生态环境、人工植物种群、食草人工动物种群、食肉人工动物种群从t=ta时刻后小于其临界值,考察人工生态系统AE的演变结果。汇总并分析全部实验的结果,总结人工生态系统失衡的演变规律。 图3所示是一个失衡态人工生态系统的演变实验。图3中的各个子图展示了人工生态系统AE在模拟气候从t=ta1和t=ta3两个不同时刻起小于其临界值的情况下,人工生态系统AE从底层到最顶层演变的详细过程,其中,ta1< ta3。在图3a中,AE(ta1)=1,模拟气候生态层分别从ta1和ta3两个不同的时刻后小于其临界值,其变化过程如图3a所示。 Figure 3 An unbalanced artificial ecosystem evolution experiment图3 一个失衡态人工生态系统的演变实验 图3a中,模拟气候C(t)的变化范围具体表达如下: 根据式(5)可知人工生态环境V1(t)的变化过程如图3b所示,其变化范围可表达为: 对应图3b的变化,根据式(6)可知人工植物种群yp(t)的变化过程如图3c所示,可见,yp(ta1)=yp(L),yp(tp)=ypmin,但此后yp(t) 虽然模拟气候C(t)在[ta2, ta3]时段恢复平衡,不再小于其临界值,但不能改变人工生态系统演变的趋势。因此,AE(t)=0,t∈(ta1, t2]。 其它的生态层如人工生态环境、人工植物种群、食草人工动物种群从t=ta时刻小于其临界值的演变案例与图3类似,都能引起其上面的所有生态层小于其临界值,并最终导致人工生态系统从t=ta时刻起开始失衡。 5.2 人工生态系统开始失衡及恢复平衡的条件 定理4(失衡定理)已知人工生态系统在t=ta时刻处于平衡态,即AE(ta)=1;但若从t=ta起,人工生态系统AE中任一生态层小于其临界值,则从t=ta时刻起,人工生态系统必将开始失衡,即AE(t)=0,t∈(ta, ta+Γc]。 证明穷举法。 若yc(ta)= yc(L),但yc(t)< yc(L),根据定义4,则AE(t)=0, t∈(ta, ta+Γc]。 若yh(ta)= yh(L),但yh(t)< yh(L),则yc(ta)=yc(L),且yc(t)< yc(L),根据定义4,则AE(t)=0, t∈(ta, ta+Γc]。 若yp(ta)= yp(L),但yp(t) 若V1(ta)= V1(L),但V1(t) 若C(ta)= C(L),但C(t) □ 定理4说明,人工生态系统是非常脆弱的,不管是底层、中间层、最顶层,任一生态层小于其临界值都会导致人工生态系统开始失衡。 定理5(足量补缺定理)若AE(ta)=0,对于所有小于临界值的人工生命种群生态层,在ta时刻从人工生态系统的外界补充缺省量△y,使该生态层达到其临界值,且在[ta, ta+△t]时段内保持C(t)≥C(L),则AE(t)=1,t∈[ta, ta+△t]。 证明令AE(ta)=0时,所有小于临界值的人工生命种群生态层为y(ta),其它人工生命种群生态层为y′(ta),显然y′(ta)≥y(L);由于对于所有y(ta),外界补充的缺省量△y= y(L)-y(ta),所以y(ta)= y(ta)+△y= y(L),而y′(ta)≥y(L),又C(t) ≥C(L),故V1(t) ≥V1(L),所以AE(t)=1,t∈[ta, ta+△t]。 □ 定理5说明,对于失衡态人工生态系统,如果没有外界的干预,即使模拟气候和人工生态环境生态层可以重新恢复为平衡,但人工生态系统仍然失衡,这种现象称为人工生态系统的失衡是不可逆的。 定理5的指导意义在于,对于失衡态人工生态系统,如果促使模拟气候不再小于其临界值,并且从外界增加足量人工生命种群当量,则处于失衡态的人工生态系统可以恢复为平衡态人工生态系统,这种措施称为足量补缺。 由于人工生态系统AE是对经典生态系统的真实模拟,因此,上述平衡态及失衡态人工生态系统演变的结论揭示了生态系统演变的规律。 基于人工生命种群的人工生态系统演变研究改正了现有生态系统演变研究存在的缺陷。提出的基于人工生命种群的人工生态系统是自然生态系统的模拟,组成成分丰富,可以涵盖任意生态系统的所有成分,其研究结果能够反映生态系统演变的一般规律,具有通用性;算法模型中采用的大量参数都是取自于已有的统计数据,算法模型本身为明确的数学公式,演变的过程借助计算机模拟快速实现,因而相应的研究周期短,研究结果时效性强;研究充分体现了气候对生态系统的影响,把模拟气候作为人工生态系统的底层,并有模拟气候的算法模型,其它生态层的算法模型也和模拟气候的算法模型相关联,人工生态系统演变的实验也是以模拟气候的变化作为输入量。通过研究,不但发现了平衡态人工生态系统存在的收窄现象,确定了平衡态人工生态系统的变化范围,而且推导出了平衡态人工生态系统继续保持平衡的决定条件;研究发现了平衡态人工生态系统开始失衡的原因,并给出了失衡态人工生态系统恢复平衡的条件;研究确定了模拟气候在人工生态系统演变中的决定作用,描述了各个生态层之间的相互影响。 本文研究的局限性是所研究的人工生态系统只包括一条生态链,对于含有多条生态链的复杂人工生态系统的演变,我们将立足于单链人工生态系统,以期去揭示更多人工生态系统演变的规律。 [1] Johnson J B, Omland K S. Model selection in ecology and evolution[J]. Trends in Ecology & Evolution, 2004, 19(2):101-108. [2] Street G M, Laubach T A. And so it grows:Using a computer-based simulation of a population growth model to integrate biology & mathematics[J]. American Biology Teacher, 2013, 75(4):274-279. [3] Yan Hui-zhen, Ma Zhi-en, Liu Yan. β Persistence and β extinction of a predator-prey Lotka-Volterra model of two species[J]. Chinese Journal of Engineering Mathematics, 2010,27(1):139-144.(in Chinese ) [4] Li Xiang, Li Zhi-xiang. Strong periodic solution for a class of non-local PDE models for population dynamics with state-selective delays[J]. Acta Mathematica Scientia, 2011,31(3):709-719.(in Chinese ) [5] Levin S A, Grenfell B, Hastings A, et al. Mathematical and computational challenges in population biology and ecosystems science[J]. Science, 1997, 275(5298):334-343. [6] Ma C, He J. Gallopin system in a polluted environment[M]∥Advances in Computer Science, Intelligent System and Environment,2011:443-446. [7] Liu Meng,Wang Ke,Liu Xian-wei,et al.Long term behaviors of stochastic single-species growth models in a polluted environment[J].Applied Mathematical Modelling,2011,35(2):752-762. [8] Klemmer A J, Wissinger S A, Greig H S, et al. Nonlinear effects of consumer density on multiple ecosystem processes[J]. Journal of Animal Ecology, 2012, 81(4):770-780. [9] Lehodey P, Senina I, Sibert J, et al. Preliminary forecasts of Pacific bigeye tuna population trends under the A2 IPCC scenario[J]. Progress in Oceanography, 2010, 86(1):302-315. [10] Cao M, Woodward F I. Dynamic responses of terrestrial ecosystem carbon cycling to global climate change[J]. Nature, 1998, 393(6682):249-252. [11] Langton C G. Artificial life:An overview[M]. Cambridge:The MIT Press, 1997. [12] de Garis H. An artificial brain ATR’s CAM-brain project aims to build/evolve an artificial brain with a million neural net modules inside a trillion cell cellular automata machine[J]. New Generation Computing, 1994, 12(2):215-221. [13] Hornby G S, Pollack J B. Evolving L-systems to generate virtual creatures[J]. Computers & Graphics, 2001, 25(6):1041-1048. [14] Terzopoulos D.Artificial life for computer graphics[J]. Communications of the ACM, 1999, 42(8):32-42. [15] Tu X,Terzopoulos D.Artificial fishes:Physics, locomotion, perception, behavior[C]∥Proc of the 21st Annual Conference on Computer Graphics and Interactive Techniques, 1994:43-50. [16] Tomita M, Hashimoto K, Takahashi K, et al. E-CELL:Software environment for whole-cell simulation[J]. Bioinformatics, 1999, 15(1):72-84. [17] Wang Rong-fang, Jiao Li-cheng, Liu Fang, et al. Nature computation with self-adaptive dynamic control strategy of population size[J]. Journal of Software, 2012,23(7):1760-1772.(in Chinese) [18] Raymond M, Rousset F. GENEPOP(version 1.2):Population genetics software for exact tests and ecumenicism[J]. Journal of Heredity, 1995, 86(3):248-249. [19] Ameca J, Mace G M, Cowlishaw G, et al. Natural population die-offs:Causes and consequences for terrestrial mammals[J]. Trends in Ecology & Evolution, 2012, 27(5):272-277. [20] Wall D H, Bardgett R D, Behan-Pelletier V,et al. Soil ecology and ecosystem services[M]. Oxford:Oxford University Press, 2012. [21] Deagle B E, Jones F C, Chan Y F, et al. Population genomics of parallel phenotypic evolution in stickleback across stream-lake ecological transitions[J]. Proceedings of the Royal Society B:Biological Sciences, 2012, 279(1732):1277-1286. [22] Moss R H, Edmonds J A, Hibbard K A, et al. The next generation of scenarios for climate change research and assessment[J]. Nature, 2010, 463(7282):747-756. [23] Tang Guo-li,Ding Yi-hui,Wang Shao-wu, et al. Comparative analysis of the time series of surface air temperature over China for the last 100 years[J]. Advances in Climate Change Research, 2009,5(2):71-78.(in Chinese) [24] Both C, van Turnhout C A M, Bijlsma R G, et al. Avian population consequences of climate change are most severe for long-distance migrants in seasonal habitats[J]. Proceedings of the Royal Society B:Biological Sciences, 2010, 277(1685):1259-1266. [25] Canellas L P, Balmori D M, Médici L O, et al. A combination of humic substances and Herbaspirillum seropedicae in- oculation enhances the growth of maize(Zea mays L.)[J]. Plant and Soil, 2013,366(1-2):119-132. [26] Fridley J D, Grime J P. Community and ecosystem effects of intraspecific genetic diversity in grassland microcosms of varying species diversity[J]. Ecology, 2010, 91(8):2272-2283. [27] Spencer W, Rustigian-Romsos H, Strittholt J, et al. Using occupancy and population models to assess habitat conservation opportunities for an isolated carnivore population[J]. Biological Conservation, 2011, 144(2):788-803. 附中文参考文献: [3] 阎慧臻,马知恩,刘燕.捕食-被捕食二维Lotka-Volterra模型的β持续生存与β绝灭[J].工程数学报,2010,27(1):139-144. [4] 李祥,李志祥.一类种群动力学中具有状态选择时滞的非局部偏微分方程的强周期解[J].数学物理学报,2011,31(3):709-719. [17] 王蓉芳,焦李成,刘芳,等.自适应动态控制种群规模的自然计算方法[J].软件学报, 2012,23(7):1760-1772. [23] 唐国利,丁一汇,王绍武,等.中国近百年温度曲线的对比分析[J].气候变化研究进展,2009,5(2):71-78. FENGKang,born in 1968,MS,associate professor,his research interests include cognitive science, and artificial life. Researchonartificialecosystemevolutionbasedonartificiallifepopulation FENG Kang (Department of Computer and Information Engineering,Huainan Normal University,Huainan 232038,China) To find the principles of ecosystem evolution through artificial life technology,an artificial life population equivalent model is proposed.An artificial ecosystem based on artificial life population is created. The artificial ecosystem includes simulated climate,artificial ecological environment, artificial plant population,artificial herbivore population and artificial carnivore population from the bottom layer to the top layer.A large number of artificial ecosystem evolution experiments are conducted.The experimental results demonstrate that the time of maximum value turns short from the bottom layer to the top layer when the artificial ecosystem is balanced,but the value of per layer is not beyond the maximum value and less than the critical value.In balanced conditions,the artificial ecosystem keeps balanced if the simulated climate is higher than the critical value, and the artificial ecosystem does not keep balanced any more when any layer is under the critical value in any moment. In unbalanced conditions, the artificial ecosystem is irreversible except that the shortage of values is added to the critical value from the outside of the artificial ecosystem.The artificial ecosystem evolution research based on artificial life population corrects the flaw of the former ecosystem evolution research and finds the principles of ecosystem evolution,so it is a scientific approach to ecosystem evolution research. artificial life population;artificial ecosystem;critical value;balanced condition;unbalanced condition 1007-130X(2014)11-2174-12 2013-11-04; :2014-09-16 国家自然科学基金资助项目(11401243) TP181 :A 10.3969/j.issn.1007-130X.2014.11.021 冯康(1968),男,安徽淮南人,硕士,副教授,研究方向为认知科学和人工生命。E-mail:fenglikanglcq@163.com 通信地址:232038 安徽省淮南市淮南师范学院计算机与信息工程系 Address:Department of Computer and Information Engineering,Huainan Normal University,Huainan 232038,Anhui,P.R.China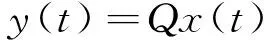
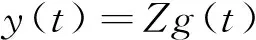
3 基于人工生命种群的人工生态系统的构成
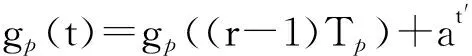
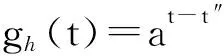
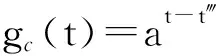
4 平衡态人工生态系统演变的研究
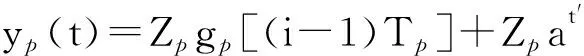
5 失衡态人工生态系统演变的研究
6 结束语

