无线传感器网络中三方密钥建立协议研究*

2014-09-13郑明辉刘召召

计算机工程与科学 2014年11期

关键词：敌手会话密钥

郑明辉，刘召召

(湖北民族学院信息工程学院，湖北恩施 445000)

无线传感器网络中三方密钥建立协议研究*

郑明辉，刘召召

(湖北民族学院信息工程学院，湖北恩施 445000)

提出了一个无线传感器网络(WSN)的可证明安全认证三方密钥建立协议。协议的安全性基于求解椭圆曲线离散对数问题和双线性配对Diffie-Hellman问题的计算不可行性。节点之间的身份验证是无线传感器网络中最具挑战性的一个安全要求，它需要在WSN中三个相邻节点之间建立正确的会话密钥轮来实现这种安全目标。通过理论证明,该协议对数据完整性攻击和会话密钥中已知密钥安全性攻击是安全的，并提供了完美的前向安全。

双线性配对;密钥交换;会话密钥

1 引言

无线传感器网络WSN(Wireless Sensor Networks)是由大量部署在监测区域内的廉价微型传感器节点组成，通过无线通信方式形成的一个多跳的自组织网络系统，其目的是协作地感知、采集和处理网络覆盖区域中被感知对象的信息，并发送给观察者。传感器、感知对象和观察者构成了无线传感器网络的三个要素。

目前国内外关于WSN密钥建立协议的研究主要分为基于身份的密钥体制和基于证书的密钥体制。王圣宝等人[1]利用 Gentry 的基于身份的加密方案提出了第一个标准模型下可证安全性的密钥建立协议，但其无会话密钥托管模式下的密钥建立协议不能满足PKG(Private Key Generator)前向安全性，恶意的密钥生成中心PKG能计算出所有的会话密钥。随后汪小芬等人[2]对文献[1]的协议进行了改进，改进后的协议能够满足基于身份的标准安全模型下的安全属性，同时能够防止前后向安全性和 PKG前向安全性。

Li Z等人[3]提出基于ECDH(Elliptic Curve Diffie-Hellman)的密钥交换协议，该协议实现了通信双方的身份认证以及会话密钥的协商，采用隐式认证方式，有效地减少了通信两端公钥P的计算开销。随后一种基于ECDH的可认证密钥建立协议[4]也被提出，该方案在ECDH协议的基础上作了改进，能够实现通信双方相互认证，同时可以有效抵御中间人攻击。

无线传感器网络通常部署在敌对的环境中，它们会遇到各种各样的恶意攻击。无线传感器网络中收集的数据信息是有价值的，应当保密。为了保护这个传输信息或消息，任何三个相邻传感器节点之间的密钥建立协议和相互的身份验证协议成为无线传感器网络的必备条件。由于先天的限制，比如说低功率、较少的存储空间、低计算能力和较短的传感器节点通信范围，大多数传统协议在任意三个相邻传感器节点之间建立认证多密钥通过采用密钥预先分配的方法。然而，这些技术都有漏洞。随着加密技术的快速发展，最近的研究结果表明，椭圆曲线密码ECC(Elliptic Curve Cryptography)适用于网络资源有限的无线传感器网络。基于椭圆曲线密码学的加密系统对传感器网络尤其适应，因为它们比任何其他公钥技术具有更高效的资源利用率[5～8]。传感器节点的计算能力有限，所有传统公钥密码学的模幂运算是必需的,因此不能在无线传感网络上实现。幸运的是，与其他公钥加密系统相比，椭圆曲线加密系统具有显著的优点[9,10]，比如说较小的密钥尺寸、更快的计算速度。因此，基于椭圆曲线加密的密钥建立协议比其他加密系统更适合资源约束型的传感器节点。

2 基于ECC的三方密钥建立协议

下面给出本文要用到的符号和系统参数：

(1)P是阶为n的椭圆曲线E上的一个生成元，满足n×P=Ο，q是一个大素数，Ο是一个无穷远处的点。

(2)q是群的阶。

(3)SKi，1≤i≤8，是建立在三个节点之间的会话密钥。

(4)Qi是传感器节点i的公钥。

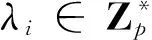
定义1设G1与G2是两个循环群，并且它们都有相同的素数阶q，G1是一个加法群，G2是一个乘法群，设e是一个可计算的双线性映射，e:G1×G2→G2，如果满足下面的条件：

(2)非退化性：假设P是G1的一个生成元，那么e(P,P)就是G2的生成元。

(3)可计算性：对任意的P,Q∈G1，存在一个高效的算法来计算e(P,Q)，我们称这样的一个双线性映射e为可容许的双线性映射。

2.1 基于ECC的协议

考虑三个通信节点i、j和k，它们将建立共享会话密钥保障后续的安全通信。假定节点i已经计算出长期的公私钥对Qi=λi·P，类似地，节点j的长期公私钥对为Qj=λj·P，节点k的长期公私钥对为Qk=λk·P。三方的共享会话密钥集通过节点i、j和k协同计算出来，具体过程如下：

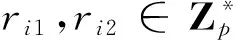
(1)

节点i将元组{Vi1,Vi2,Si,Cert(Qi)}发送给节点j和k。

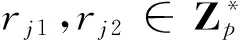
(2)

节点j将元组{Vj1,Vj2,Sj,Cert(Qj)}发送给节点i和k。

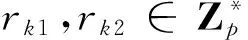
(3)

节点k将元组{Vk1,Vk2,Sk,Cert(Qk)}发送给节点i和j。

步骤4节点i从Vj1和Vj2中提取x向量Xj1和Xj2，从Vk1和Vk2中提取向量Xk1和Xk2，并通过式(4)和式(5)验证接收信息是否正确。

(4)

(5)

如果式(4)和式(5)均成立，则节点i计算出下面的会话密钥集：

SK1=ri1Vj1Vk1

SK2=ri1Vj1Vk2

SK3=ri1Vj2Vk1

SK4=ri1Vj2Vk2

SK5=ri2Vj1Vk1

SK6=ri2Vj1Vk2

SK7=ri2Vj2Vk1

SK8=ri2Vj2Vk2

步骤5类似地，节点j从Vi1和Vi2中提取x向量Xi1和Xi2，从Vk1和Vk2中提取x向量Xk1和Xk2，并通过式(6)和式(7)验证接收信息是否正确。

(6)

(7)

如果式(6)和式(7)均成立，则节点j计算出下面的会话密钥集：

SK1=rj1Vi1Vk1

SK2=rj1Vi1Vk2

SK3=rj1Vi2Vk1

SK4=rj1Vi2Vk2

SK5=rj2Vi1Vk1

SK6=rj2Vi1Vk2

SK7=rj2Vi2Vk1

SK8=rj2Vi2Vk2

步骤6类似地，节点k从Vi1和Vi2中提取x向量Xi1和Xi2，从Vj1和Vj2中提取向量Xj1和Xj2，并通过式(8)和式(9)验证接收信息是否正确。

(8)

(9)

如果式(8)和式(9)均成立，则节点k计算出下面的会话密钥集:

SK1=rk1Vi1Vj1

SK2=rk1Vi1Vj2

SK3=rk1Vi2Vj1

SK4=rk1Vi2Vj2

SK5=rk2Vi1Vj1

SK6=rk2Vi1Vj2

SK7=rk2Vi2Vj1

SK8=rk2Vi2Vj2

2.2 基于ECC协议的安全性分析

本文提出的三方密钥建立协议的安全性是基于椭圆曲线离散对数的难解问题。下述定理1和定理2表明，该协议可以抵御传感器节点上数据完整性的攻击且会话密钥具备前向安全性。

定理1本文提出的基于椭圆曲线密码学ECC的三方密钥建立协议可以抵抗数据完整性的攻击，当且仅当在椭圆曲线离散对数问题ECDLP(Elliptic Curve Discrete Logarithm Problem)是难解的。

证明三个节点中的任意两个节点i和j，节点i通过通信信道发送敏感数据到节点j，敌手改变或处理这个数据，然后通过依靠错误的会话密钥欺骗这个诚实的节点。敌手将会计算Si去验证已核实的式(4)来欺骗节点j，敌手能够随机选择两个点Vi1和Vi2，并提取出对应的x向量Xi1和Xi2;之后，敌手不得不在椭圆曲线上找一个μ去满足等式μ·P=Qi-Xi1Vi1-Xi2Vi2，为了计算出椭圆曲线上的μ，它就要求敌手解决椭圆曲线离散对数问题。因此，敌手去伪造一个有效的信息去欺骗节点j在计算上是不可行的。

□

定理2本文提出的基于ECC的三方密钥建立协议对一个敌手来说生成正确的会话密钥在计算上是不可行的，即使先前的会话密钥已泄露。

证明三个节点中的任意两个节点i和j，在协议的每一轮节点i和j选择全新的随机数通过等式(1)和式(2)计算Si和Sj。这意味着这四个生成会话密钥是不同的，不取决于协议的每一轮执行。敌手获得协议每一轮的随机数在计算上是不可行的，因为需要计算会话密钥。因此，提出的协议可以抵抗对已知的密钥攻击。

3 基于双线性配对的三方密钥建立协议

3.1 基于双线性配对的协议

考虑三个通信节点i、j和k，它们将建立共享会话密钥。假定节点i已经计算出长期的公私钥Qi=λi·P，类似地，节点j的长期公私钥为Qj=λj·P，节点k的长期公私钥为Qk=λk·P。共享会话密钥集通过节点i、j和k协同计算出来，具体过程如下：

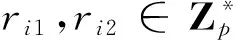
(10)

节点i将元组{Vi1,Vi2,Si,Cert(Qi)}发送给节点j和k。

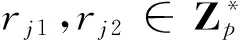
(11)

节点j将元组{Vj1,Vj2,Sj,Cert(Qj)}发送给节点i和k。

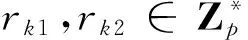
(12)

节点k将元组{Vk1,Vk2,Sk,Cert(Qk)}发送给节点i和j。

步骤4节点i从Vj1和Vj2中提取x向量Xj1和Xj2，从Vk1和Vk1中提取x向量Xk1和Xk2，并通过式(13)和式(14)验证接收信息是否正确。

(13)

(14)

如果式(13)和式(14)均成立，则节点i计算出下面的会话密钥集：

SK1=e(ri1Vj1Vk1,Qj+Qk)

SK2=e(ri1Vj1Vk2,Qj+Qk)

SK3=e(ri1Vj2Vk1,Qj+Qk)

SK4=e(ri1Vj2Vk2,Qj+Qk)

SK5=e(ri2Vj1Vk1,Qj+Qk)

SK6=e(ri2Vj1Vk2,Qj+Qk)

SK7=e(ri2Vj2Vk1,Qj+Qk)

SK8=e(ri2Vj2Vk2,Qj+Qk)

步骤5类似地，节点j从Vi1和Vi2中提取x向量Xi1和Xi2，从Vk1和Vk2中提取x向量Xk1和Xk2，并通过式(15)和式(16)验证接收信息是否正确。

(15)

(16)

如果式(15)和式(16)均成立，则节点j计算出下面的会话密钥集：

SK1=e(rj1Vi1Vk1,Qi+Qk)

SK2=e(rj1Vi1Vk2,Qi+Qk)

SK3=e(rj1Vi2Vk1,Qi+Qk)

SK4=e(rj1Vi2Vk2,Qi+Qk)

SK5=e(rj2Vi1Vk1,Qi+Qk)

SK6=e(rj2Vi1Vk2,Qi+Qk)

SK7=e(rj2Vi2Vk1,Qi+Qk)

SK8=e(rj2Vi2Vk2,Qi+Qk)

步骤6类似地，节点k从Vi1和Vi2中提取x向量Xi1和Xi2，从Vj1和Vj2中提取x向量Xj1和Xj2，并通过式(17)和式(18)验证接收信息是否正确。

(17)

(18)

如果式(17)和式(18)均成立，则节点k计算出下面的会话密钥集：

SK1=e(rk1Vi1Vj1,Qi+Qj)

SK2=e(rk1Vi1Vj2,Qi+Qj)

SK3=e(rk1Vi2Vj1,Qi+Qj)

SK4=e(rk1Vi2Vj2,Qi+Qj)

SK5=e(rk2Vi1Vj1,Qi+Qj)

SK6=e(rk2Vi1Vj2,Qi+Qj)

SK7=e(rk2Vi2Vj1,Qi+Qj)

SK8=e(rk2Vi2Vj2,Qi+Qj)

3.2 基于双线性配对协议的安全分析

下述定理3表明，提出的基于双线性配对协议可以抵御传感器节点上数据完整性的攻击。

定理3提出的基于双线性配对密钥建立协议可以抵抗数据完整性的攻击，当且仅当在椭圆曲线离散对数问题(ECDLP)是难解的。

证明三个节点中的任意两个节点i和j，节点i通过通信信道发送敏感数据到节点j，敌手改变或处理这个数据，然后通过依靠错误的会话密钥欺骗这个诚实的节点。敌手将会计算Si去验证已核实的式(4)来欺骗节点j;然后，敌手能够随机选择两个点Vi1和Vi2，并提取出对应的x向量Xi1和Xi2，之后，敌手不得不找一个Si去满足等式e(Si,P)=e(Xi1Vi1+Xi2Vi2,Vi1)·e(Vi2,Qi)，但是对敌手来说,在不知道式(1)中λi的情况下,去计算Si是不可行的。对敌手来说，为了从已知的Qi中计算出λi，它就要求敌手解决椭圆曲线离散对数问题。因此，敌手伪造一个有效的信息去欺骗节点j在计算上是不可行的。

□

4 结束语

在本文中,我们为无线传感器网络提出了一种新型结构的三方密钥建立协议，这种无线传感器网络中的每个节点所需的存储空间是固定的。传感器节点通过保护后续会话密钥可以与其他相邻节点建立安全通信，即使先前的会话密钥被管理者泄露。这个协议对完美的前向密钥保密和修改攻击是安全的。所提出的协议提供了两个重要的优势：(1)每个节点所需的内存空间是固定的，所以它在无线传感器网络中是兼容的。(2)通过保护后续会话密钥，传感器节点与其他相邻节点可以建立安全通信。

[1] Wang Sheng-bao，Cao Zhen-fu，Dong Xiao-lei. Provably secure identity-based authenticated key agreement protocols in the standard mode[J]. Chinese Journal of Computers，2007, 30(10):1842-1854. (in Chinese)

[2] Wang Xiao-fen, Chen Yuan, Xiao Guo-zhen. Analysis and improvement of an ID-based authenticated key agreement protocol[J].Journal on Communications, 2008, 29(12):16-21. (in Chinese)

[3] Li Z, Zhan G, Ye X. Towards an anti-inference (k，l)-anonymity model with value association rules[C]∥Proc of the 17th International Conference on Database and Expert Systems Applications, 2006:883-893.

[4] Nogueira M, Silva H, Santos A, et al. A security management architecture for supporting routing services on WANETs[J]. IEEE Transactions on Network and Service Management, 2012, 3(8):1-13.

[5] Hankerson D,Menezes A,Vanstone S.Guide to elliptic curve cryptography[M]. Berlin:Springer, 2004.

[6] Kar J, Majhi B. A secure two-party identity based key exchange protocol based on elliptic curve discrete logarithm

problem[J]. Journal of Information Assurance and Security, 2009, 5(1):473-482.

[7] Koblitz N. Elliptic curve cryptosystem[J]. Mathematics of Computation, 1987, 48(17):203-209.

[8] Miller V S. Use of elliptic curves in cryptography[C]∥Proc of the Advances in Cryptology-Crypto’85, 1985:417-426.

[9] Dai D Y, Xu H B. Key predistribution approach in wireless sensor networks using LU matrix[J]. IEEE Sensors Journal, 2010, 10(8):1399-1409.

[10] Zhang P, Zhang Y T. Analysis of using interpulse intervals to generate 128-bit biometric random binary sequences for securing wireless body sensor networks [J]. IEEE Transactions on Information Technology in Biomedicine, 2012, 16(1):176-182.

附中文参考文献：

[1] 王圣宝, 曹珍富, 董晓蕾. 标准模型下可证安全的身份基认证密钥协商协议[J]. 计算机学报, 2007, 30(10):1842-1852.

[2] 汪小芬，陈原，肖国镇.基于身份的认证密钥协商协议的安全分析与改进[J]. 通信学报, 2008, 29(12):16-21.

ZHENGMing-hui,born in 1972,PhD,professor,CCF member(E200029016M),his research interest includes information security.

刘召召(1990),男,湖北孝感人，硕士生，研究方向为信息安全。E-mail:990922923@qq.com

LIUZhao-zhao,born in 1990,MS candidate,his research interest includes information security.

Researchontripartitekeyestablishmentprotocolforwirelesssensornetworks

ZHENG Ming-hui,LIU Zhao-zhao

(College of Information Engineering,Hubei Minzu University,Enshi 445000,China)

A provably secure authenticated multiple key establishment protocol for Wireless Sensor Networks (WSNs) is proposed.Security of the protocol is based on the computational infeasibility of solving elliptic curve discrete logarithm problem and computational Diffie-Hellman problem on bilinear pairing.The authentication among the nodes is one of the most challenging security requirements in WSNs.To achieve this security goal, it is required to establish a correct session key among the three adjacent nodes of WSNs. It is proved that the proposed protocol is secure against the attacks on data integrity and the known key security attacks on session key.It also provides perfect forward secrecy.

bilinear pairing;key exchange;session key

1007-130X(2014)11-2132-05

2014-06-11;

：2014-08-15

国家自然科学基金资助项目(61173175)；湖北省杰出青年基金资助项目(2012FFA006)

TP393.08

：A

10.3969/j.issn.1007-130X.2014.11.013