不动点方法及其在压缩感知核磁共振成像中的应用
2014-09-12刘晓曼丛佳朱永贵
刘晓曼,丛佳,朱永贵
(中国传媒大学理工学部理学院,北京 100024)
1 引言
压缩感知理论指出:如果信号在某个变换域是稀疏的或可压缩的,就可以利用一个与变换基不相关的观测矩阵将变换所得的高维信号投影到一个低维空间上,根据这些少量的观测值,通过求解凸优化问题就可以实现信号的精确重构。此理论有效地减少了采集系统的复杂度,降低了系统的成本,加快了图像采集速度。压缩感知成像在医疗诊断方面起到了很重要的作用,特别是核磁共振成像的应用。核磁共振成像技术(Nuclear Magnetic Resonance Imaging,简称NMRI),又称磁共振成像(Magnetic Resonance Imaging,简称MRI),被广泛应用于医学诊断中,极大地推动了医学、神经生理学和认知神经科学的迅速发展。由大量资料调查表明,减少扫描时间即减少核磁共振成像所需要的时间是极其重要的,这就意味着在保证图像质量的情况下,要尽可能少地从频域中收集观测数据。然而,这看上去直接违背了长期以来建立的奈奎斯特标准,即所获得的观测数据的数量必须至少与恢复图像所需要的信息数量相匹配。这就意味着完美的图像重构将是不可能的,但压缩传感允许我们在没有相关噪声的情况下重构图像。
本文主要将不动点连续性(Fixed Point Continuation,简称FPC)[1][2]方法应用到压缩感知的核磁共振图像中,通过不动点定理高效的重构出图像,并通过数值实验证明,核磁共振图像可以从全部数据的40%-50%抽样中几乎精确重构。
2 预备知识
2.1 压缩感知理论
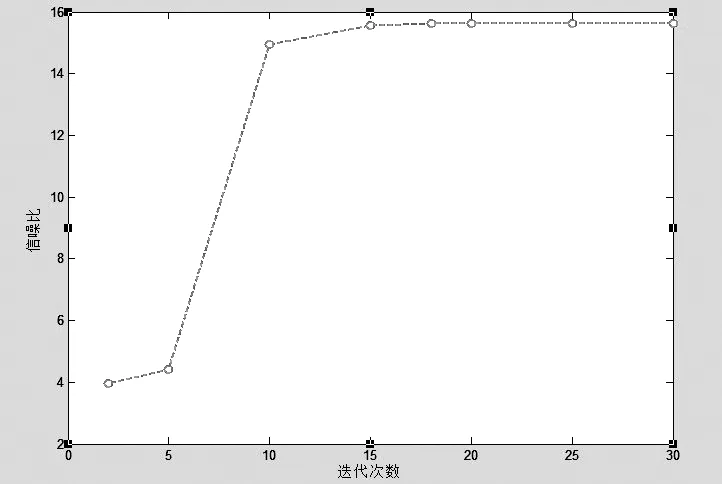
设向量u代表一个图像,一个压缩算法,例如,通过找到某一变换φ(例如傅里叶或小波基)来压缩这个图像,使得φu=x是(近似)稀疏的。为了恢复u,我们使用相同的变换,并且设u=φ-1x。
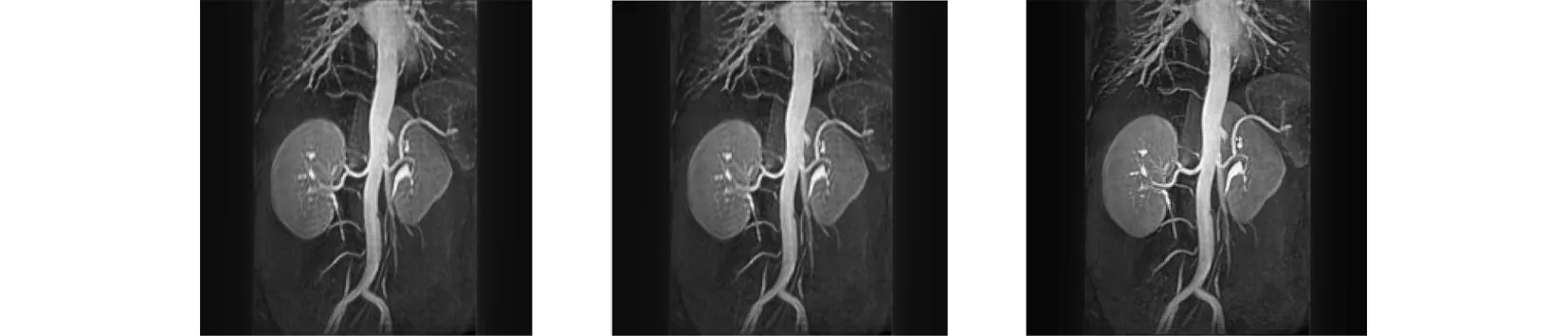
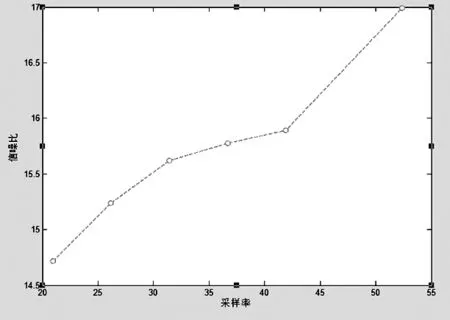
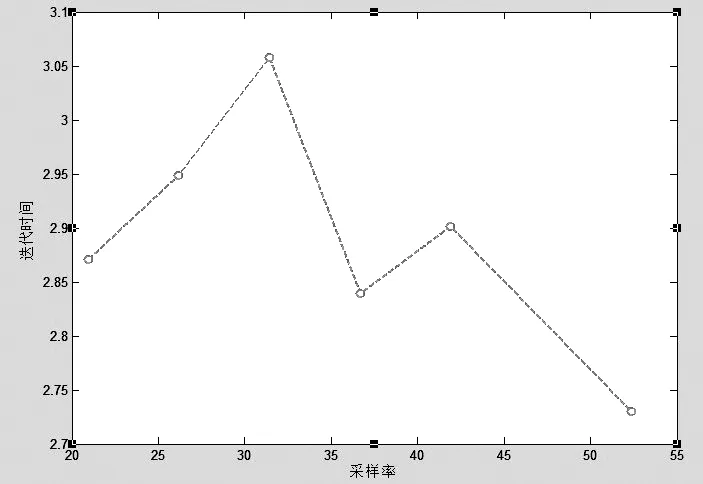
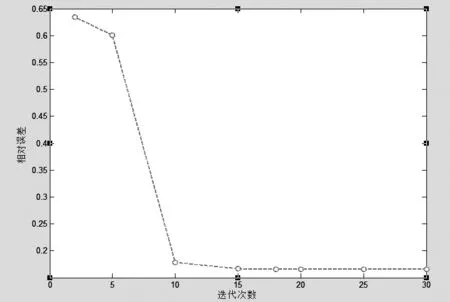
压缩感知的全部过程包括三步:编码、传感和解码。在第一步中,通过一个线性变换R,u被编码成一个维数较小的向量b=Ru,其中b的维数为m,x的维数为n,m 所以在压缩感知的过程中,三大核心问题是运用压缩感知理论的关键问题。信号的可稀疏表示是压缩感知的先验条件[3]。而在已知信号是可压缩的前提下,压缩感知过程可分为两步: (1)设计一个与变换基不相关的m×n(m≪n)维测量矩阵对信号进行观测得到m维的测量向量。 (2)由m维的测量向量重构信号。 稀疏的数学定义:信号x∈Rn在正交基ψ下的变换系数向量为Ө=ψTX,假如对于0 (1) 则说明系数向量Ө在变换域ψ下是稀疏的。 广义地,如果Ө中非零元素的个数为K,则信号X称为K-稀疏的。 测量矩阵,又称传感矩阵,从压缩传感整个过程可以看出,传感矩阵起着相当重要的作用。它的选择合适与否,既关系到能否达到压缩的目的,又直接关系到信号能否被精确重构,此研究工作已有初步成果[4]。就矩阵选取而言,目前常用的传感矩阵是随机矩阵,如高斯矩阵、贝努力矩阵、傅里叶随机测量矩阵、非相关测量矩阵等,它们已经被验证满足UUP特性[4]。 至于传感矩阵的构造,则首先需要研究传感矩阵与重构算法的关系。在重构算法中,常用的匹配追踪算法[5]、正交匹配追踪算法等的重构质量与传感矩阵有着密切的联系。所以,如果能构造出性质好的矩阵,将大大简化重构算法的步骤,并提高信号的重构质量。 从本质上讲,压缩感知理论中的信号重构问题就是寻找欠定方程组的最稀疏解的问题。设u为传统采样得到的信号,长度为n,而通过压缩感知则直接得到b,长度为m(m 如果未知的其它信息,则上述逆问题很难求得唯一解。但若信号u是K稀疏的,设m≥K·log(n),则上述方程组可以求解,通过下式求最稀疏的向量,从而获得u: (2) 其中‖·‖0表示u中非零元素的个数。然而,尽管从理论上来讲,这种方法可以实现,但是在实际中不可行,因为这是一个组合问题(NP难问题),计算量非常大。因此我们需要寻求合适的范数来近似求解上述问题。采用l1范数最小化求得的解,为稀疏向量,非常接近最小化l0范数所得的真实解。因此,我们可以选择l1范数最小化来近似求解上述优化问题,从而可将一个非凸优化问题转化为凸优化问题。即 (3) 我们需要将信号变换到变换域考虑。设φ是压缩基(如小波基)或紧框架,满足规范正交,即φ*φ=I,作变换φu=x,显然x是稀疏的。于是在这种情况下的求解方法为: (4) 其中A=Rφ-1。 以上考虑的都是等式约束,然而实际中,测量过程可能会引入噪声,这时约束条件(4)式中的Ax=b必须被放松,从而引出问题 (5) 或者问题 (6) 因为f(x)为凸函数,定义X*为(6)的最优解集。通过凸分析理论[6]可知(6)的最优化条件为 x*∈X*⟺0∈SGN(x*)+μg(x*) (7) 0是Rn中的零向量,g(x)=▽f(x),SGN(x)为多重符号函数(集值函数) 我们的算法基于算子分裂法。由凸分析理论[6]可以知道,求凸函数φ(x)的最小值问题相当于找到次微分∂φ(x)的零值。大多数情况下φ可以分裂成两个凸函数φ=φ1+φ2。这意味着T可以分裂成两个最大单调算子的和,即:T=T1+T2。对于τ>0,如果T2是单值的,I+τT1是可逆的,则可得到: 0∈T(x)⟺0∈(x+τT1(x))-(x-τT2(x)) ⟺(I-τT2)x∈(I+τT1)x ⟺x=(I+τT1)-1(I-τT2)x. (8) 式(8)得到了找到T的零点的向前向后分裂算法: xk+1=(I+τT1)-1(I-τT2)xk (9) 对于最小值问题(6),对应以上理论的具体函数表达式为 φ1(x)=‖x‖1,φ2(x)=μf(x), T1=∂‖·‖1,T2=μ▽f 且对于(I+τT1)-1,通过[17]可知道,(I+τT1)-1是分段的收缩算子,即软阈值。 命题X*是(6)的最优解集。对于任何标量τ>0,x*∈X*当且仅当 (10) 解方程(10),从而解决(6)的最小值问题,很自然考虑到不动点的迭代 xk+1=sv·h(xk)v=τ/μ (11) 虽然我们通过完全不同的逼近得到不动点迭代上式,但后来我们发现这只是向前向后分裂法,当T1(x)=∂‖x‖1/μ,T2(x)=g(x)通过简单的计算可以得到: sv=(I+τT1)-1,h=I-τT2。 (12) 其中κ(HEE)是HEE的条件数,满足当|E|很小时,可以使HEE小于H。这就意味着稀疏性可以加快收敛速度。 对于本文算法的观测值b定义为 b=Axs+ (13) 为了收敛平稳,在BB方法下直接自动默认为非单调线性搜索,即选择一个α使迭代 xk+1=xk+a(sv∘h(xk)-xk) 这种线性搜索结合Armijo型步长条件,即得本文算法(FPC和BB steps方法和非单调线性搜索的结合算法)。 在我们的实验中,由R估量得出的傅里叶系数并不是在随机的频率中选取的。我们是通过以下方式来选择的:在k-space中,我们采取的采样方式是沿着一定数量的从中心散开、呈辐射状的直线来选取,即半径抽样。例如图1、图2分别显示了在一个k-space中的22×2、22×5条辐射状直线(是对210×210的大脑原始图像进行抽样时的采样情况),即这些分别是44views、110views抽样频域图。 图1 采样率20.95% 图2 采样率52.38% 所有实验都是在MATLAB 7.8.0版本上运行的。执行运算的笔记本电脑是AMD turion X2 Dual-Core Mobile RM-72 处理器,3.00GB的内存。在MATLAB中,基于FPC编码[1]之上,并对FPC方法进行加强,利用BB步和线性搜索方法,将其应用到了真实的二维核磁共振图像上。 我们在四张不同的方形二维核磁共振图像上检测我们的编码。这四张图像分别是:210×210的大脑原始图像、220×220的肾脏动脉MR原始图像。在所有的检测问题中,采用的噪声是均值为0方差为0.01的高斯白噪声。对这些图像分别进行44views、110views频域抽样,重构的图像如图3、图4所示。每组图中图(a)为原始图像图(b)、(c)为恢复后图像。 在数值试验中,相对误差(Relative Error)和信噪比(Signal to Noise Rations,简称SNR)用来评估重构图像的质量。相对误差和信噪比的定义如下: (14) (15) (a) (b) (c)图3 (a)是原始大脑图像;(b)、(c)是恢复后的图像,它们的采样率分别是20.95%、52.38% (a) (b) (c)图4 (a)是原始大脑图像;(b)、(c)是恢复后的图像,它们的采样率分别是20.95%、52.38% MRI图像Views/采样率Rerr/相对误差SNR/信噪比(dB)迭代时间(秒)210×210的大脑MR原始图像22×2/20.95%0.187314.71812.792422×3/31.43%0.165615.62002.979622×5/52.38%0.158715.98982.9484220×220的肾脏动脉MR原始图像22×2/20%0.157816.03982.839222×3/30%0.147216.64202.839222×5/50%0.105319.54893.2916220×220的胸部MR原始图像22×2/20%0.114018.86072.823622×3/30%0.100020.00313.073222×5/50%0.096220.33782.9952256×256的心脏原始图像22×2/17.19%0.257611.78144.258822×3/25.78%0.233912.61964.243222×5/42.97%0.204013.80624.2588 图5 相对误差与采样率之间的关系 图6 信噪比与采样率之间的关系 图7 迭代时间与采样率之间的关系 对于同一个图像,同样的采样率下,不同的迭代次数下,信噪比和相对误差的变换。以210×210的大脑原始图像在66views频域抽样为例,结果如表2: 表2 图8 相对误差与迭代次数之间的关系 图9 信噪比与迭代次数之间的关系 图10 迭代时间与迭代次数之间的关系 在本篇论文中,基于压缩感知理论,我们使用不动点定理(FPC)的最小化模型,通过较少数量的观测数据来恢复核磁共振图像,使不动点定理很好的运用到了核磁共振图像的重构中,得到了一个有效的算法。在真实的几幅正方形的核磁共振图像上进行的数值实验表明,这种算法可以在相对采样率较小的情况下,用不到一分钟的时间来恢复忠实于原图的正方形图像。通过对相对误差、信噪比、迭代时间和迭代次数的对比,我们知道,在迭代15次左右基本达到效果。无需达到最大迭代次数。在采样率在40%-50%时,信噪比和相对误差成平稳趋势,达到精确重构。而通过利用最优化的技巧,例如线性搜索等,可使算法的速度加快。然而,本文并没有对不动点定理的收敛速度进行系统的分析,对这种方法的理论分析也缺乏详细的研究,这些问题都有待以后再解决。 [1] T H Elaine,Wotao Yin,Yin Zhang. A Fixed-Point Continuation Method for l1-Regularized Minimization with Applications to Compressed Sensing[R]. CAAM Technical Report TR07-07,2007. [2] T H Elaine,Wotao Yin,Yin Zhang. Fixed-point Continuation Applied To Compressed Sensing:Implementation and Numerical Experiments[J]. Journal of Computational Mathematics,2010,28(2):170-194. [3] 张雄伟,黄建军,朱 涛.信息处理领域的创新理论——压缩感知[J].军事通信技术,2011,32(4):83-97. [4] 赵瑞珍.压缩传感与稀疏重构的理论及应用[DB/OL].http://www.paper.edu.cn,中国科技论文在线. [5] Neff R,ZAkhor A.Very Low bit rate video coding based on matching pursuits[J].IEEE Transactions on Circuits and Systems for Video Technology,1997,7(1):158 -171. [6] Rockafellar R. Convex Analysis[M].Princeton:Princeton University Press,1970. [7] Chambolle A,DeVore R A,N-Y Lee,et al. Nonlinear wavelet image processing:variational problems,compression,and noise removal through wavelet shrinkage[J]. IEEE Transactions on Image Processing,1998,7(3):319-335. [8] Barzilai J, Borwein J. Two point step size gradient methods[J].IMA J Numer Anal,1988,8(1):141-148.2.2 信号的稀疏表示

2.3 测量矩阵的构造
2.4 重构算法的设计

3 主要算法
3.1 最优性和最优解集
3.2 不动点算法
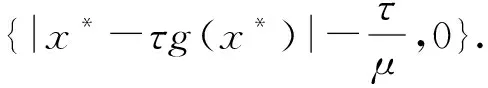
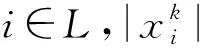

3.3 增强的不动点算法
4 数值实验


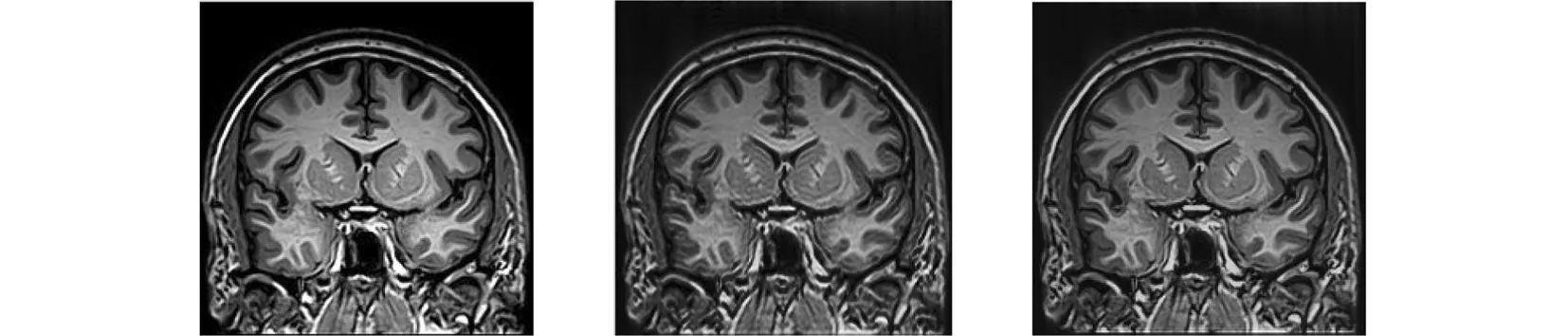




5 结论
