30×104 m3LNG冷箱跑冷损失的计算①

崔新亭 张 钊

(1.中空能源设备有限公司 2.上海理工大学制冷技术研究所)

30×104m3LNG冷箱主要由一台板翅式换热器和冷箱壳体组成，两者中间充填珠光砂绝热层。在传统的换热器中，来自外部的传热影响通常略去不计。而LNG换热器的最低工作温度可达-160 ℃左右，与环境温度有着近200 ℃的温差。它与环境之间的传热现象不能忽视，原因在于温差的存在使得在冷箱运行的过程中，部分热量会通过冷箱保温层进入换热器，从而对低温液体LNG的产量造成不利影响，这部分热量就是冷箱的跑冷损失Q。跑冷损失不仅浪费低温冷能，而且严重时还会导致系统无法实现低温状态，以致使系统无法正常工作。低温换热器的跑冷损失主要包括3个方面：一是冷箱与换热器及管道之间的气体导热与对流换热；二是冷箱到换热壁的导热，即冷桥；三是冷箱与换热器及管道之间的辐射换热。对于LNG低温冷箱，冷箱到换热壁的导热为跑冷损失的主要部分。

Mohd Zaki Abidina采用MATLAB编程对大型LNG主低温换热器进行建模，对其内部各换热单元的换热特性进行分析[1]。Ho-Myung Chang等人运用HYSYS软件对混合制冷剂液化流程中的多股流换热器(一冷流、二热流)进行性能模拟，并讨论了模拟结果用于实际设计的可行性[2]。西安交通大学的余峰对氦制冷系统冷箱内部真空绝热条件下的辐射换热规律以及辐射对换热器表面温度分布的影响进行了计算和研究，结果表明，辐射跑冷的影响使换热器温度分布偏差最高达4 K，采用铝箔辐射屏绝热的方法能很好地减少辐射跑冷[3]。而对于混合制冷剂液化流程中LNG冷箱的跑冷损失计算，目前国内外相关研究较少，在实际的工程应用中，通常将跑冷损失按主换热器热负荷的0.5%以上计，对流程计算结果进行修正。

本文通过采用类比法、数学模型法、有限元法3种方法对30×104m3LNG冷箱的跑冷损失进行计算，并对计算结果进行了比较分析。

1 LNG冷箱结构及主要运行数据

图1为LNG的冷箱示意图。图中E1为板翅式换热器，其尺寸如图所示，冷箱壳体和E1之间为珠光砂保温层，其中E1侧面保温层厚度为1 m，端部保温层为2 m。由于珠光砂是多孔粉末结构，保温层内的换热可认为是通过热传导完成的。

LNG冷箱在工作过程中，热流体从E1顶部向下流动，冷流体从E1底部向上流动，两者在E1内部进行换热，由于板翅式换热器的高效换热特性，冷热流体在每个换热截面的温度比较接近，因此，在计算跑冷损失时，按照冷流体的温度计算，不会造成不合理偏差。图1左侧8个节点0～7，将E1等距离分为7段，每段间距1 m。

表1、表2的数据为我公司30×104m3LNG项目的计算数据，这些数据与LNG冷箱的跑冷损失计算相关。表1为计算的热力学数据，表2为E1各节点冷流体的温度设计值ti。

表1 热力学数据

表2 E1各点温度设计值

2 计算方法

2.1 LNG冷箱跑冷损失的类比计算

由于LNG冷箱的工作温度范围与空分设备接近，因此，用类比空分设备的跑冷损失计算方法进行计算。空分设备的跑冷损失通常按参考文献[4]中式(12-2)计算，计算方法如下：

(1)

式中，Q为跑冷损失，VK为加工空气流量，其中约1/3的跑冷损失加在主换热器上。

由于LNG冷箱只有换热器E1，如果计算E1的跑冷损失，可将式(1)改为如下方程：

(2)

式中，F为表1热流体流量，m3/h。

将表1中的参数代入式(2)，可得Q=9 514.503 W。

2.2 LNG冷箱跑冷损失的数学模型法计算

2.2.1数学模型推导

为了便于分析跑冷损失的换热状况，先对LNG冷箱做如下规定：

(1) 可以将冷箱壁的温度设置为50 ℃[5]。由于冷箱壁的导热能力远大于保温层的导热能力，因此，可以假设保温层的外表面与冷箱壁温度相等，即tw=50 ℃。

(2) 根据冷箱的实际运行效果，保温层下端表面温度取tg=20 ℃。

(3) 主换热器E1为板翅式换热器，任一截面处的温度与冷流体温度相同。E1各节点之间截面h的温度同截面h与节点之间的距离呈线性关系，各相邻节点之间的距离为1 m，截面h温度方程如下：

(3)

式中，h为截面h到节点i的距离，th为截面h的温度。其中i=0～6。

对(3)式进行简化，可得

th=ti+(ti+1-ti)h,i=0～6

(4)

(4) E1每一水平截面为等温截面。

(5) 冷箱无泄漏，E1及保温层的内部沿高度方向的传热忽略不计。

沿换热器的任一位置截取冷箱截面，见图2。图中网状剖面的区域仅仅接触换热器的棱边，接触面积可忽略不计，经该区域传导的热量所占比重极少，大部分热交换发生在与换热器侧面平行的那部分保温层。显然，如果忽略网状剖面的区域，保温层的外侧和换热器侧表面之间的换热可简化为平壁导热模型。同上，冷箱的顶部和底部的换热可按同样的换热模型进行计算。根据文献[6]中的式(2-19)，对于表面积为A的平壁，两侧表面各自维持均匀温度的平板，其导热方程如下:

(5)

式中，Q为热量，W；A为平壁表面积，m2；λ为珠光砂导热系数，这里取λ=0.045 W/(m·K)；δ为壁厚，m。

根据图1，冷箱的跑冷损失由3部分组成，顶部Q1，底部Q2，侧面Q3，则总的跑冷损失计算如下:

Q=Q1+Q2+Q3

(6)

根据图1、表2及式(5)可得到冷箱两端的跑冷损失，Q1=0.814 W，Q2=7.2 W。

由于换热器E1侧面的温度沿高度方向发生变化，因此，不能直接利用式(5)进行计算，需要单独做分析。

2.2.2跑冷损失Q3的计算

根据假设条件，沿E1高度的任一截面h的温度可按式(4)计算，若取截面h的高度为dh，则截面的侧面面积为A=(1.2+1.5) ×2dh=5.4dh(m2)，该截面处保温层壁厚δ=1 m，λ=0.045 W/(m·K)。

根据图1、表2及式(5)，可写出E1侧面跑冷损失Q3的微分方程：

dQ3=5.4dh×0.045(tw-th)=0.243×(50-th)dh

将式(4)代入，经整理得到

dQ3=(12.15-0.243(ti+(ti+1-ti)h))dh

(7)

由于每两个节点i、i+1之间的长度都是1 m，则将式(7)在每段中进行积分，并将这些积分值进行累加，即可得到Q3的方程：

对h进行积分，可得如下积分：

经整理，可得

(8)

将表2中的数据代入式(8)，则可得Q3=169.14 W。

将Q1、Q2、Q3的值代入式(6)，可求得LNG冷箱跑冷损失Q=176.524 W。

在考虑LNG冷箱的构成中，忽略了低温管道等元件的跑冷效应。但是就E1而言，这些忽略会使E1自身的跑冷损失增加，因此并不影响计算结果的实用性。

2.3 LNG冷箱跑冷损失的有限元模拟

若要获得更精确的计算结果，可借助有限元法进行计算。按图1的假设条件建立三维模型，计算后的等温曲线剖视图见图3。对于图2所示截面，用有限元法计算跑冷损失时，不用忽略网状剖面部分的热传导效应。图4为节点1处1/4截面等温曲线分布图，计算后得到的跑冷损失为Q=244.23 W。

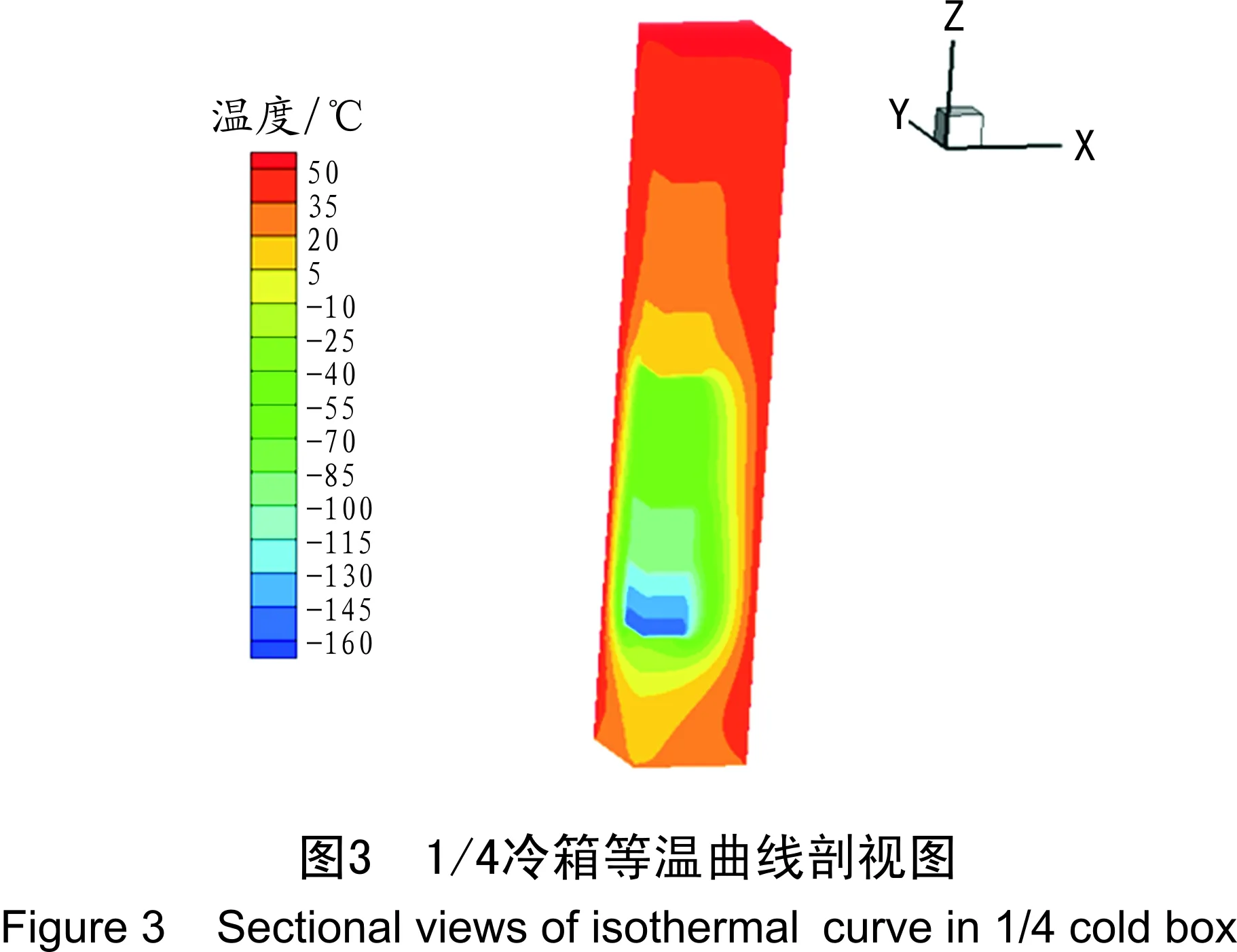
3 LNG冷箱跑冷损失的比较与分析

将LNG冷箱的跑冷损失Q的3种计算结果进行对比，并分别与表1中E1的热负荷QE1进行比较，结果见表3。

由表3可以看出，使用数学模型法和有限元法进行计算的结果比较接近。这表明，在理想状态下，两者均反映了LNG冷箱真实的跑冷损失。但是，其计算结果与空分类比法有较大差距，这两种计算方法能否直接应用到实际设计中去，仍需讨论。

在流程计算过程中，如果计算结果的修正参数只有跑冷损失的话，不仅需要考虑文中所述跑冷损失的影响，还需要考虑泄漏、摩擦等不可逆损失对计算结果的影响。换句话说，流程计算结果中的跑冷损失是以上多种因素造成的当量值。表3中空分类比法的计算结果实际上是跑冷损失的当量值，这也是其与另外两种计算结果偏差较大的原因，这在空分设备的工程应用中已得到广泛验证。

表3 跑冷损失计算结果比较

4 结 论

流程计算过程中的跑冷损失是为修正计算结果而引入的当量值。由于LNG冷箱和空分设备冷箱的工作温度基本相同，利用空分类比法计算的当量跑冷损失对其应该有较大的参考价值，在实际的设计过程中，还需要进行进一步的探讨和验证。

参考文献

[1] Mohd Zaki Zainal Abidina. Development of the liquefaction unit for higher LNG production through performance optimization of main cryogenic heat exchanger (MCHE) [C]// National Postgraduate Conference (NPC), Kuala Lumpur, 2011.

[2] Chang Ho-Myung. Effect of multi-stream heat exchanger on performance of natural gas liquefaction with mixed refrigerant [J]. Cryogenics, 2012, 52(12):642-647.

[3] 余锋,厉彦忠,祝银海. 低温冷箱跑冷损失及其对内部换热器温度分布的影响[J]. 低温工程, 2005,148 (6):15-19.

[4] 张祉祐. 低温技术原理与装置[M].下册.北京:机械工业出版社,1985.

[5] 寿比南. 固定式压力容器安全技术监察规程(3.9.3)[M].北京: 新华出版社, 2010.

[6] 杨世铭，陶文铨. 传热学[M].北京: 高等教育出版社, 2003