块系覆岩中摆型波传播对巷道支护动力响应影响
2014-09-11王凯兴孟村影
王凯兴,孟村影,杨 月,李 祁
(辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000)
块系覆岩中摆型波传播对巷道支护动力响应影响
王凯兴,孟村影,杨 月,李 祁
(辽宁工程技术大学 力学与工程学院,辽宁 阜新 123000)
为研究支护体自身的动力响应规律,通过理论和计算分析岩体中的非线性摆型波传播对巷道支护动力响应的影响,根据摆型波在非连续自应力块系上覆岩体中传播时的支护动力响应模型,研究上覆岩块间的黏弹性性质及岩块破坏对支护动力响应的影响。通过计算分析得出,上覆岩块间弹性下降时,支护的动态受拉和受压幅值随之下降且周期变大;上覆岩块间阻尼增大时,支护的受拉和受压周期不变,但周期内的微扰动逐渐消失且幅值略有下降;上覆岩块沿垂直冲击方向破裂成两个子块时,支护的受拉和受压次数增加。
冲击地压;块系岩体;摆型波;支护动力响应
冲击地压是煤矿生产中的灾害之一,进入深部开采后,冲击地压动力灾害将越来越严重,深部开采中巷道支护在冲击作用下的响应规律对防冲控制具有重要意义。同时,在深部岩体工程出现了一系列新的特征科学现象,且用传统的连续介质力学理论无法圆满解释[1],如摆型波现象。Sadovsky[2]提出深部岩体等级块系构造理论。Kurlenya等[3]基于深部岩体等级块系构造理论和地下爆炸试验得到岩体的一种新的动力响应现象,称为摆型波。Kurlenya等[4]从实测岩爆、化爆和块体模型施加脉冲载荷试验中分离出摆型波波形。Aleksandrova等[5-8]基于具有软弱夹层的一维钢杆模型在冲击作用下的应力波传播试验,证明了摆型波的存在。并对各质量杆的峰值速度和加速度衰减进行了研究,Slepyan[9-10]和Kurlenya等[11-12]分别对动力传播过程中由线性和非线性弹簧以及弹性块体组成的周期块体系统进行建模分析,对波的传播特性波谱特征以及非驻波过程等进行了初步的理论分析。我国学者也对块系岩体动力响应特性做了相关研究[13-17]。但目前在摆型波传播理论和试验研究中还不能充分考虑支护的作用。同时,岩体中的摆型波传播对巷道支护动力响应研究具有一定的工程实践意义。
目前在煤矿支护方面,如木支护、锚杆(锚索)支护、锚网支护、喷浆支护、型钢棚支护以及液压支架支护等,都是按准静态围岩压力进行设计的[18-20]。对动力作用下的支护响应规律认识还存在不足。因此,由Sadovsky的观点[2],同时考虑上覆岩体和巷道支护,潘一山等[21]建立了非连续块系上覆岩体与支护系统动力模型(图1),并从支护端岩块动力响应的角度提出了防冲吸能支护,但并没有分析支护体自身的动力响应。本文在此模型基础上研究摆型波传播时支护体自身的动力响应。分析上覆岩块间黏弹性变化及支护端岩块破坏时在摆型波传播过程中支护的动力响应。
1 块系上覆岩体与支护动力模型
在图1的块系上覆岩体与支护动力模型中支护体简化为支撑上覆块系岩体的弹性体且与上覆岩块ms相固连具有支护刚度ks。块系上覆岩体由n+1个岩块组成,岩块相比于块体间的软弱连接介质可抽象为刚体,其质量为mi(i=1,2,…,n,s),块体间的软弱连接介质简化为Kelvin-Voigt模型具有黏性阻尼ci以及弹性系数ki(i=1,2,…,n),初始块体受冲击载荷f(t)作用。岩块间的黏弹性体在块体自身重力作用下会发生一定的变形而达到静力平衡,图1中的虚线位置为静力平衡位置。设在达到静力平衡时,由于黏弹性体的变形而使第1块岩块产生的位移量为δ1。
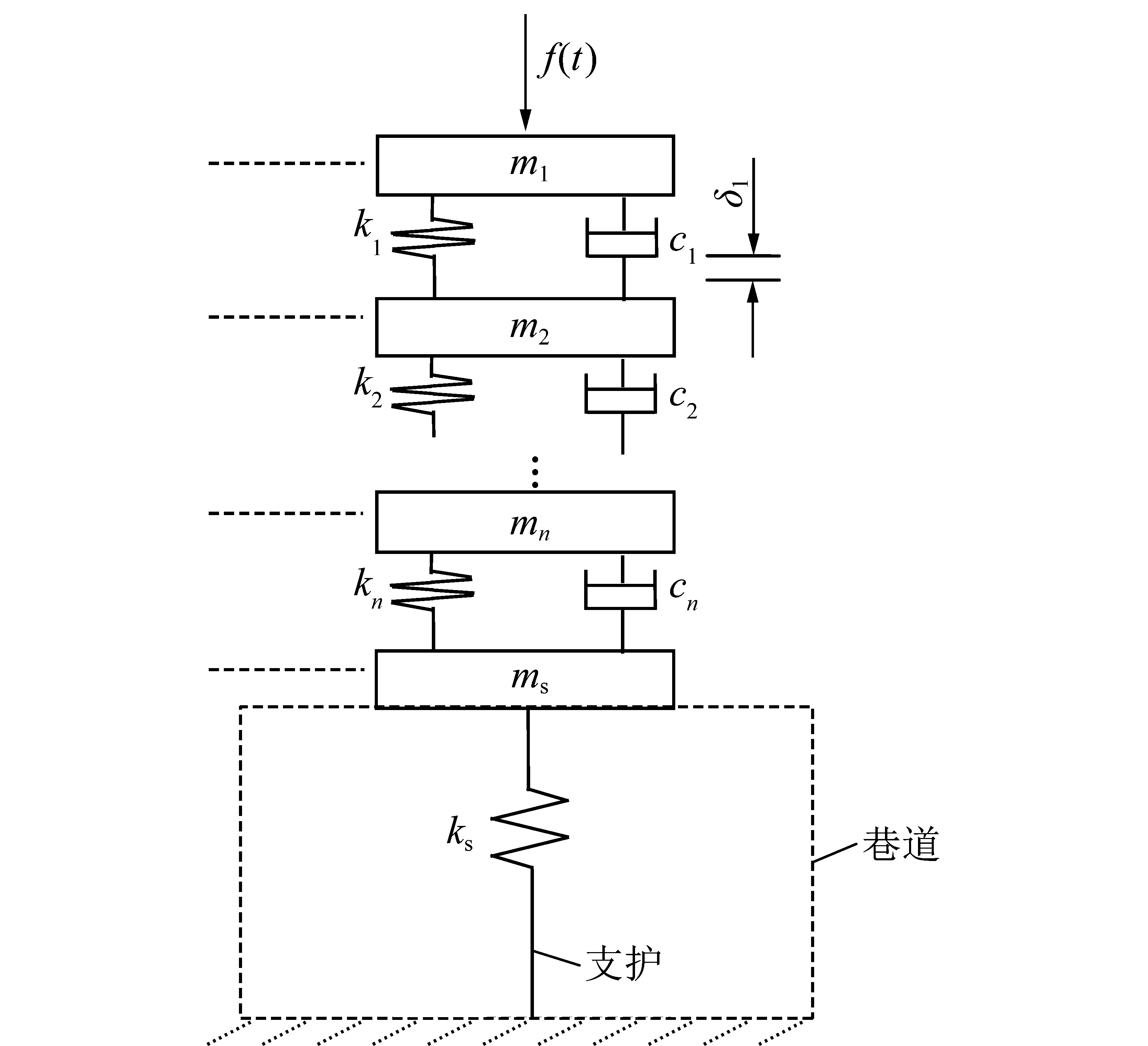
图1 块系上覆岩体与支护动力模型Fig.1 Dynamic model of overburden rock blocks and support
在冲击载荷f(t)作用下块系上覆岩体中摆型波传播时岩块与支护动力响应微分方程为

(1)
式中,

x为块系岩体位移向量,x=[x1,…,xn,xs]T;F(t)为外界扰动,F(t)=[f(t),0,…,0]T;δ=[δ1,…,δn,δs]T;g=[g,…,g]T。
根据静力平衡条件,有
mig=ki-1(δi-δi-1)-ki(δi+1-δi)=
(2)
将式(2)代入式(1)可得
(3)
式(3)可表示为
(4)

(5)

则在脉冲扰动f(t)作用下,式(5)的解为

(6)
式中,矩阵Φ由2n+2阶非对称实矩阵B-1A的广义特征向量φi所组成,即B-1Aφi=φi/λ;d=diag(eλ1t,eλ2t,…,eλ2n+2t),λi为广义特征向量φi所对应的特征值;q0=a-1ΦTAy(0),y(0)为初始条件,a=ΦTAΦ=diag(a1,a2,…,a2n+2)。
在瞬时脉冲扰动f(t)作用下初始条件为

即初始岩块的扰动速度为v。此时,向量y(t)便是块系上覆岩体中各岩块的位移和速度响应。
支护的形变量Δxs由支护端岩块(顶板)和底板的相对位移(xN-xs)所决定,其中,xN为底板位移,假设在冲击作用下底板固定不动,于是
(7)
由于支护为弹性体则支护的动力响应可表示为
(8)
(9)
式中,Fr为支护端上覆岩块对支护的作用力;Ff为底板对支护的作用力;ms为支护体的质量;a′为支护加速度。
因此,支护的加速度响应为
(10)
由式(10)可知,当支护形变量Δxs一定时,可以通过调节支护刚性与支护质量的比值来控制支护在冲击作用下的加速度响应。同时,支护在动力作用下的拉伸和压缩位移极值亦是支护在拉伸和压缩方向上的受力极值点。当支护体一定时,ks/ms便是一个常数,其加速度响应只与Δxs有关。
2 摆型波传播过程支护动力响应
通过计算分析摆型波传播时上覆岩块mn和ms之间的力学性质变化及岩块ms破坏时对支护动力响应的影响。根据相关试验参数[8],选取原始计算参数为
mi=10 kg,ki=105kg/s2,(i=1,…,n,s);
ci=20 kg/s,(i=1,…,n)
初始条件为

2.1 上覆岩块间弹性变化时支护形变量响应
为便于分析,采用10个上覆岩块进行计算,则支护端岩块ms=m10,由式(6)和式(7)可得在原始计算参数下支护的形变量Δxs,如图2所示。
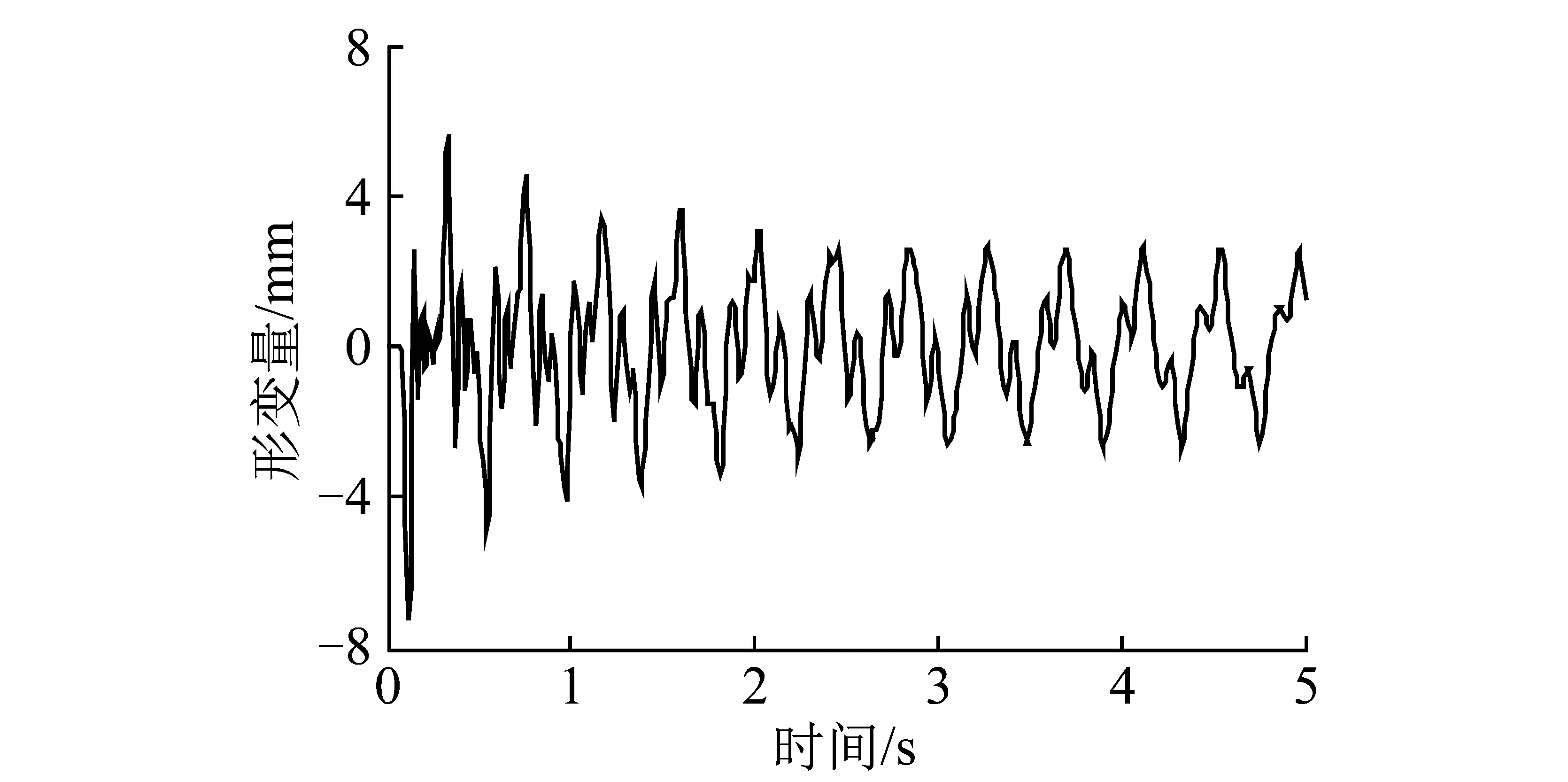
图2 原始计算参数下支护形变量Fig.2 Deformation of support on original calculate parameters
图2给出了脉冲扰动f(t)诱发摆型波在块系上覆岩体中传播时,支护在前5 s内的形变量响应。支护形变量具有周期衰减规律且2 s后衰减较慢。在整个时间历程上有11.5个衰减周期,分别经历了12次周期最大拉伸和周期最大挤压变化,且最大拉伸量为5.7 mm,最大压缩量为7.5 mm。同时从图2可以看出,支护的周期受拉和受压极值点分布较密集。
下面分析岩块m10和岩块m9之间的弹性下降对支护形变量响应的影响,通过计算分析弹性系数k9分别为原来的1/10,1/50,1/100,即k9=1×104,2×103,1×103kg/s2,其余计算参数不变,则支护体的形变量Δxs如图3所示。
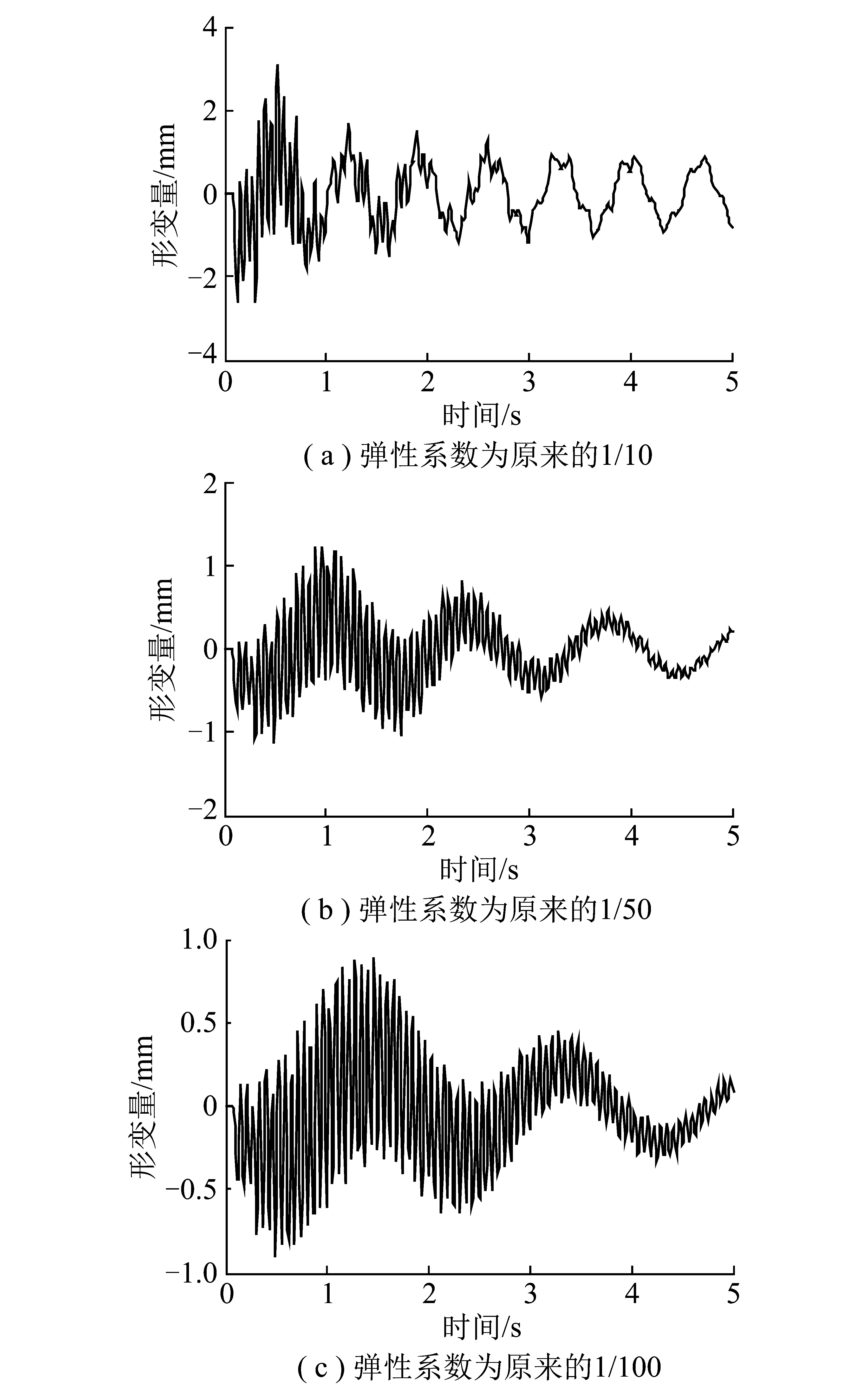
图3 岩块间弹性系数下降时支护形变量Fig.3 Deformation of support when rock block partings elasticity decrease
由图3(a)可知,当弹性系数为原来的1/10时,支护形变量幅值有所下降,且衰减周期变大。整个时间历程上有7个衰减周期,分别经历了7次周期最大拉伸和8次周期最大挤压变化,且最大拉伸量为3.1 mm,最大压缩量为2.6 mm。同变化前(图2)相比最大压缩量下降明显,且支护周期受拉和受压极值点分布相对稀疏。
由图3(b)可知,当弹性系数为原来的1/50时,支护形变量幅值下降明显,且衰减周期变大。整个时间历程上有3.5个衰减周期,分别经历了4次周期最大拉伸和最大挤压变化,且最大拉伸量为1.3 mm,最大压缩量为1.1 mm。与图3(a)相比,最大拉伸量和最大压缩量均明显下降。同时支护的周期受拉和受压极值点分布更加稀疏。
由图3(c)可知,当弹性系数为原来的1/100时,支护形变量幅值下降幅度进一步增大,且衰减周期变大。整个时间历程上有2.5个衰减周期,分别经历了3次周期最大拉伸和最大挤压变化,且最大拉伸量为0.9 mm,最大压缩量为0.9 mm。与图3(b)相比,最大拉伸量和最大压缩量均略有下降,同时支护的周期受拉和受压极值点分布略加稀疏。
因此,降低上覆岩块间的弹性,能有效地对支护进行缓冲,保护并抑制其动力响应,但并非下降幅度越大效果越好。通过计算可知,在弹性系数下降为原来的1/50时支护的动力响应明显削弱,但弹性下降为原来的1/100时支护的动力响应相比于1/50时略有减弱,但需要付出更多的代价。所以针对一定的冲击可以根据支护的动力承载极限选择合适的弹性变化范围进行岩体卸压。
2.2 上覆岩块间阻尼变化时支护形变量响应
通过计算分析黏性系数c9分别为原来的10,50,100倍,即c9=200,1 000,2 000 kg/s,其余参数不变,则支护形变量Δxs如图4所示。

图4 岩块间阻尼增大时支护形变量Fig.4 Deformation of support when rock block partings damping increase
由图4(a)可知,当阻尼系数为原来的10倍时,支护形变量响应规律与变化前(图2)类似,但形变量曲线相对光滑,在3 s后周期内微扰动逐渐消失。同时,支护形变量的衰减周期保持不变,整个时间历程上分别经历了12次周期最大拉伸和最大挤压变化,且最大拉伸量为5.4 mm,最大压缩量为7.2 mm,与变化前(图2)相比略有下降。
由图4(b)可知,当阻尼系数为原来的50倍时,支护的形变量曲线较光滑,且在2 s后周期内微扰动逐渐消失。同时衰减周期不变,整个时间历程上支护的最大拉伸量为4.8 mm,最大压缩量为6.9 mm,与图4(a)相比均有所下降。
由图4(c)可知,当阻尼系数为原来的100倍时,支护的形变量曲线光滑且衰减较快,在2 s后周期内微扰动迅速消失。同时衰减周期不变,整个时间历程上支护的最大拉伸量为4.3 mm,最大压缩量为6.9 mm,与图4(b)相比,最大拉伸量略有下降。
因此,增大上覆岩块间的阻尼能止息支护振动进而对支护进行有效保护,但阻尼的作用在经过一段时间后才明显表现出来,具有一定的时滞性。
2.3 上覆岩块破坏时支护形变量响应
通过破坏岩块改变原有上覆岩体结构,将岩块m10沿与冲击垂直的方向均匀的破坏成两个子块,且子块间的力学特性与其余块体间的力学性质相同。此时,整个块系岩体由11个岩块组成且支护与m11相连,同时m10=ms=5 kg,k10=ks=1×105kg/s2,c10=20 kg/s,其余计算参数不变,则支护形变量Δxs(此时Δxs=-x11)如图5所示。
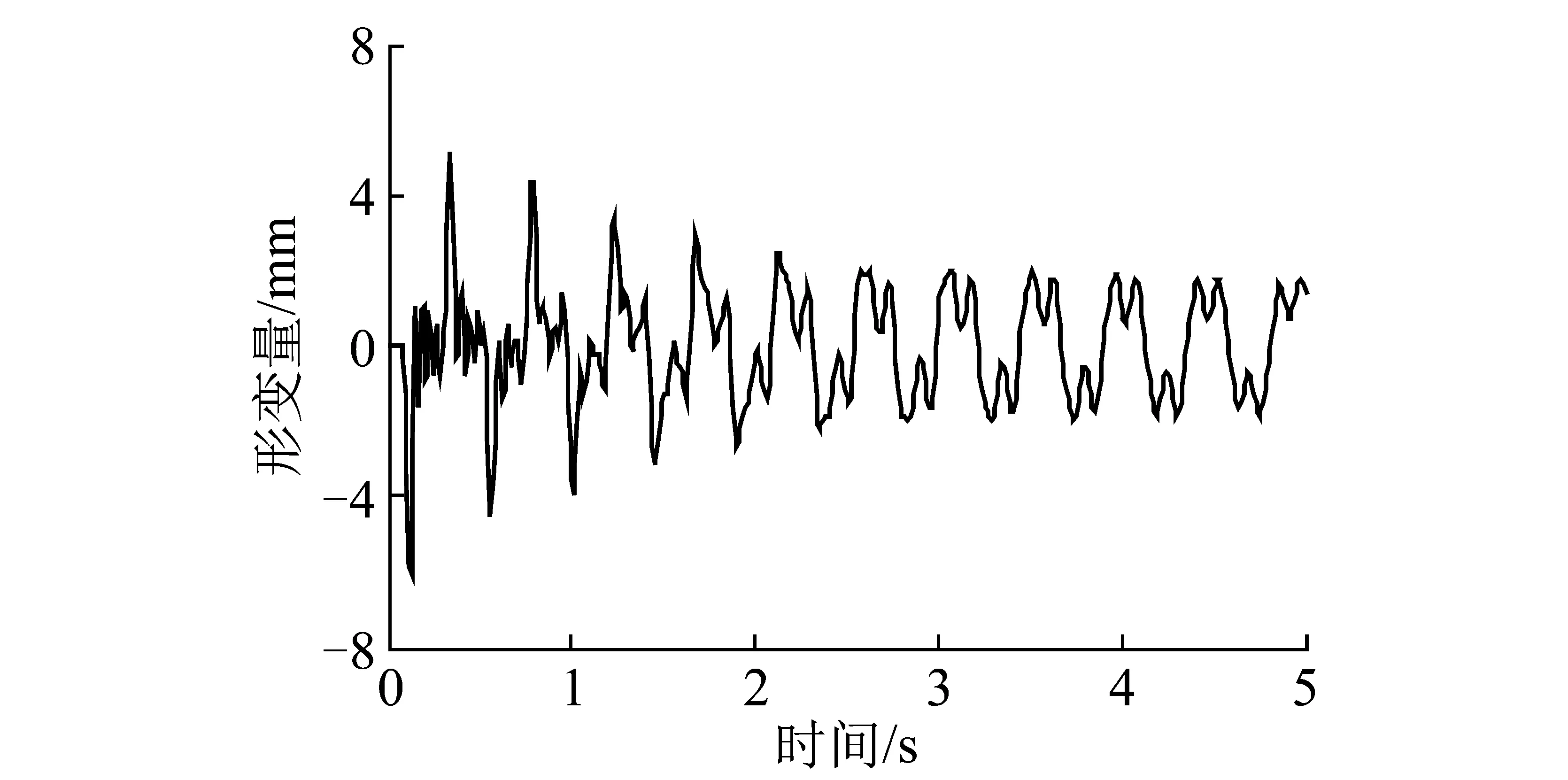
图5 上覆岩块均匀破坏时支护形变量Fig.5 Deformation of support when overburden block rock uniform fracture
由图5 可知,当岩块m10沿与冲击垂直的方向均匀的破坏成两个子块时,与变化前(图2)相比支护形变量响应幅值和周期均略有减小。此时经历了10.5个衰减周期,但2 s后周期内的波峰和波谷出现了明显的分叉,导致支护在2 s后的受拉和受压频率增加。整个衰减过程经历了17次周期最大拉伸变化和16次周期最大挤压变化,且最大拉伸量为5.3 mm,最大压缩量6.4 mm,与变化前(图2)相比有所下降。
3 结 论
(1)上覆岩块间弹性下降使得支护在动力作用下的受拉和受压周期变大且幅值明显减小。随着弹性系数的下降支护受拉和受压频率明显降低且拉伸和压缩幅值趋于对称变化。因此,降低上覆岩块间的弹性能迅速抑制支护的动力响应。
(2)上覆岩块间黏性增大时支护的受拉和受压频率保持不变,但形变量幅值有所下降且微扰动逐渐消失。同时,阻尼的作用具有一定的时滞性。当上覆岩块破坏成两个子块时,支护的受拉和受压幅值均下降,但衰减周期内的波峰和波谷出现分叉导致周期受拉和受压次数增加,对此可通过增加岩块间的阻尼来消除分叉影响。
(3)通过理论分析摆型波传播过程巷道支护的动力响应可知,降低上覆岩块间弹性和增大阻尼均能对支护进行有效的缓冲保护抑制其动力响应,但并非变化幅度越大效果越好。针对一定的冲击可以根据支护的承载极限选择合适的黏弹性变化范围进行卸压以确保支护和巷道围岩的稳定。
[1] 钱七虎.深部岩体工程响应的特征科学现象及“深部”的界定[J].华东理工学院学报,2004,27(1):1-5.
[2] Sadovsky M A.Natural lumpiness of rocks[J].Dokl Akad Nauk,1979,247(4):21-29.
[3] Kurlenya M V,Oparin V N,Vostrikov V I.Formation of elastic wave packages in the block-structured medium under impulse loading pendulum type waves[J].Dokl.Akad.Nauk SSSR,1993,333(4):1-7.
[4] Kurlenya M V,Oparin V N.Geomechanics,problems of nonlinear geomechnics part II[J].Journal of Mining Science,2000,36(4):305-326.
[5] Aleksandrova N I,Chernikov A G,Sher E N.Experimental investigation into the one-dimensional calculated model of wave propagation in block medium[J].Journal of Mining Science,2005,41(3):232-239.
[6] Aleksandrova N I,Sher E N.Modeling of wave propagation in block media[J].Journal of Mining Science,2004,40(6):579-587.
[7] Aleksandrova N I.Elastic wave propagation in block medium under impulse loading[J].Journal of Mining Science,2003,39(6):556-564.
[8] Aleksandrova N I,Sher E N,Chernikov A G.Effect of viscosity of partingsin block-hierarchical media on propagation of low-frequency pendulum waves[J].Journal of Mining Science,2008,44(3):225-234.
[9] Slepyan L I,Yakoclev Yu S.Integral transformations in nonstationary problems of mechanics[M].Leningrad:Sudostroenie,1980.
[10] Slepyan L I.Models and phenomena in fracture mechanics[M].Berlin:Springer,2002.
[11] Kurlenya M V,Oparin V N,Balmashnova E G,et al.On dynamic behaviorof “self-stressed”block media.Part I.One-dimensional mechanico-mathematical model[J].Journal of Mining Science,2001,37(1):1-9.
[12] Kurlenya M V,Oparin V N,Balmashnova E G,et al.On dynamic behavior of “self-stressed”block media.Part II.Comparison of theoretical and experimental data[J].Journal of Mining Science,2001,37(5):455-461.
[13] 王洪亮,葛 涛,王德荣,等.块系岩体动力特性理论与实验对比分析[J].岩石力学与工程学报,2007,26(5):951-958. Wang Hongliang,Ge Tao,Wang Derong,et al.Comparison of theoretical and experimental analyses of dynamic characteristics of block rock mass[J].Chinese Journal of Rock Mechanics and Engineering,2007,26(5):951-958.
[14] 吴 昊,方 秦,于冬勋.深部块系岩体摆型波现象的研究进展[J].力学进展,2008,38(5):601-609. Wu Hao,Fang Qin,Yu Dongxun.Advances in the study on pendulum-type wave phenomenon in the deep block rock mass[J].Advances in Mechanics,2008,38(5):601-609.
[15] 吴 昊,方 秦,张亚栋,等.一维块系地质块体波动特性的试验和理论研究[J].岩土工程学报,2010,32(4):600-611. Wu Hao,Fang Qin,Zhang Yadong,et al.Propagation properties of stress waves in one-dimensional geo-block medium[J].Chinese Journal of Geotechnical Engineering,2010,32(4):600-611.
[16] 潘一山,王凯兴.岩块尺度对摆型波传播影响研究[J].岩石力学与工程学报,2012,31(S2):3459-3465. Pan Yishan,Wang Kaixing.Effect study of block-rock scale on pendulum-type waves propagation[J].Chinese Journal of Rock Mechanics and Engineering,2012,31(S2):3459-3465.
[17] 王凯兴,潘一山.摆型波传播过程块系岩体频域响应反演岩块间黏弹性性质[J].煤炭学报,2013,38(S1):19-24. Wang Kaixing,Pan Yishan.Frequency domain response of block-rock mass inversion partings viscoelastic property on pendulum-type wave propagation[J].Journal of China Coal Society,2013,38(S1):19-24.
[18] 陈炎光,陆士良.中国煤矿巷道围岩控制[M].徐州:中国矿业大学出版社,1994:283-284. Chen Yanguang,Lu Shiliang.Strata controlaround coal mine roadways in China[M].Xuzhou:China University of Mining and Technology Press,1994:283-284.
[19] 康红普,王金华.煤巷锚杆支护理论与成套技术[M].北京:煤炭工业出版社,2007:13-28. Kang Hongpu,Wang Jinhua.Rock bolting theory and complete technology for coal roadways[M].Beijing:China Coal Industry Publishing House,2007:13-28.
[20] 谢文兵,荆升国,王 涛.U 型钢支架结构稳定性及其控制技术[J].岩石力学与工程学报,2010,29(S2):3744-3748. Xie Wenbing,Jing Shengguo,Wang Tao.Structural stability of U-steel support and its control technology[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(S2):3744-3748.
[21] 潘一山,王凯兴,肖永惠.基于摆型波理论的防冲支护设计[J].岩石力学与工程学报,2013,32(8):1537-1543. Pan Yishan,Wang Kaixing,Xiao Yonghui.Design of anti-scour support based on the theory of pendulum-type wave[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(8):1537-1543.
Dynamicresponseofroadwaysupportonpendulumtypewavespropagationinoverburdenblockrockmass
WANG Kai-xing,MENG Cun-ying,YANG Yue,LI Qi
(SchoolofMechanicsandEngineering,LiaoningTechnicalUniversity,Fuxin123000,China)
In order to research on dynamic response of support,the effect of propagation of nonlinear pendulum type waves on dynamic response of roadway support was analyzed by theoretical calculation.Based on the dynamic response model of support when pendulum type waves propagation on discontinuous and self-stress overburden block rock mass,the support dynamic response was studied.Dynamic response of support was analyzed through the theoretical model when changing overburden block rock partings viscoelastic property and fracture the overburden block.As the computational results,the amplitude of support tensile and compression displacement decreased and periodicity of the dynamic response increases,when block rock partings elasticity decrease.Periodicity of support displacement response invariability and weak perturbation disappears gradually when block rock partings damping increaseing,at the same time the amplitude have a slight decline.The frequency of support tensile and compression increase when the overburden block rock fractured into two subblocks on vertical direction of impact.
coal bump;block rock mass;pendulum type waves;dynamic response of support
10.13225/j.cnki.jccs.2013.2020

国家重点基础研究发展计划(973)资助项目(2010CB226803);国家自然科学基金面上资助项目(51174107)
王凯兴(1984—),男,辽宁丹东人,博士研究生。E-mail:Kaixing_wang@163.com
TD353
A
0253-9993(2014)02-0347-06
王凯兴,孟村影,杨 月,等.块系覆岩中摆型波传播对巷道支护动力响应影响[J].煤炭学报,2014,39(2):347-352.
Wang Kaixing,Meng Cunying,Yang Yue,et al.Dynamic response of roadway support on pendulum type waves propagation in overburden block rock mass[J].Journal of China Coal Society,2014,39(2):347-352.doi:10.13225/j.cnki.jccs.2013.2020
