动静加载下组合煤岩破坏失稳的突变模型和混沌机制

刘 少 虹

(1.煤炭科学研究总院 开采设计研究分院，北京 100013；2.天地科技股份有限公司 开采设计事业部，北京 100013)

动静加载下组合煤岩破坏失稳的突变模型和混沌机制

刘 少 虹1,2

(1.煤炭科学研究总院 开采设计研究分院，北京 100013；2.天地科技股份有限公司 开采设计事业部，北京 100013)

为进一步加深对动载诱发冲击地压机理的认识，采用时效损伤本构模型与尖点突变理论相结合，得到了一维动静加载下煤岩组合系统的破坏判据、突跳位移以及释放总能量的数学表达式。并建立一维动静载下煤岩组合系统的非线性动力学模型，发现外载能量与系统自身固有能量之间的相互作用导致模型的演化过程呈阶段性并出现混沌现象；当组合系统本身的非线性作用与外部载荷的作用能力相当时，系统的演化进入混沌阶段。由此得出，井下煤岩体结构与动静载荷之间的相互作用是影响动载诱发冲击地压演化过程的关键。最后，对理论结果进行一维动静加载试验验证，表明理论和试验值吻合较好。

动静加载；煤岩组合系统；突变理论；混沌理论；冲击地压

冲击地压作为煤岩动力灾害之一，已严重影响我国煤矿的安全生产。冲击地压是采场及巷道周围的煤岩体在高应力集中作用下，向采掘空间突然、猛烈冲出[1-2]。为进一步揭示冲击地压发生机理及前兆信息，常采用数值模拟或实验室试验方法，研究组合煤岩的破坏失稳特征，从而掌握顶板-煤层-底板之间的相互作用下采动诱发冲击地压的机理和规律[3-4]。其中，姜耀东等[5]对单轴加载下组合煤岩的黏滑特性进行试验分析。赵毅鑫等[6]采用红外热像、声发射等监测手段，对单轴加载下组合煤岩破坏的前兆信息进行试验分析。郭东明等[7]采用试验和数值模拟方法分析单轴和三轴加载下煤、岩交界面倾角对煤岩组合体变形破坏的影响。窦林名等[8]采用单轴循环加卸载试验，对取自4个矿的组合煤岩试样的冲击倾向性进行分析。左建平等[9]开展了单轴和三轴压缩试验，对煤岩组合试样的破坏机制和力学特性进行分析。

根据煤岩体受载形式的不同，冲击地压可分两类:一类是由于内部静载荷作用，使得煤岩体在一定范围内能量积聚超过临界值而发生的冲击地压；另一类是煤岩体内部静载荷不大，但因外部动载荷作用(如顶板断裂、断层滑动及爆破扰动等)，导致内、外载荷叠加造成的冲击地压[10-13]。从载荷的施加特点看，该类冲击地压是由动静组合载荷诱发的。以往研究组合煤岩破坏失稳大多针对的是第一类冲击地压，很少针对第二类冲击地压。

动、静加载下组合煤岩的破坏失稳是一种非线性不连续突变现象。突变理论作为一种研究自然界中不连续(跳跃性)变化现象的数学方法[14]，可被应用于分析组合煤岩体在动、静载联合作用下的失稳过程。同时，动静载下煤岩组合系统的破坏演化过程中是否存在混沌特性，产生混沌的条件是什么，混沌特性的产生和动静载荷因素之间的关系是什么？对这些问题进行分析对于动载诱发冲击地压的危险性评价和准确预测均有一定意义。

考虑到动静加载下煤岩体的破坏特征与静载下差异较大[15-18]，在分析此类问题应采用动态本构模型。目前，具有代表性的煤岩体动态本构模型，包括Bingham模型[19]、黏弹模型[20]、热力学本构模型[21]、时效损伤本构模型[22]和中应变率本构模型[23]。综合比较这些本构模型可知，时效损伤本构模型能够更好的描述煤岩体在动态破坏中的黏性和损伤特性，并能够与突变理论较好的结合。

煤矿井下的煤岩体所处应力状态较为复杂，其中一些情况，例如较窄煤柱或巷道及采场两帮浅部围岩，可近似的看作受一维垂直静载和动载荷的作用。针对此类问题，笔者首先选用时效损伤本构模型与突变理论相结合，对一维动静加载下煤岩组合系统的破坏失稳规律进行研究；并建立一维动静加载下组合煤岩的非线性动力学模型，利用混沌动力学理论对之进行深入分析；最后设计相关试验进行验证，以达到近似模拟动载诱发冲击地压的目的。通过上述分析，对动载诱发冲击地压的机理认识、有效防范和准确预测均有一定意义。

1 动静载下煤岩组合系统破坏失稳的突变理论分析

考虑到单轴加载试验中煤岩组合试样的失稳机理与实际煤岩体中发生的冲击地压有一定程度的相似，因此将煤岩组合试样视为一个统一的力学系统来研究动载扰动诱发冲击地压的动态运动过程。由煤样和岩样2个子系统组成的煤岩组合力学系统是非线性的，其特性由2个子系统的相互作用决定。显然岩样子系统在外部载荷作用下是线弹性的，它的演化直接控制着整个煤岩组合力学系统的稳定性。而煤样子系统在静载作用下需要考虑其损伤特性，而在动静组合加载下还需考虑其破坏的时效性(即黏性)。

运用突变理论可以较好地描述上述煤岩组合力学系统的动态失稳过程，从而对一维静载下煤岩组合系统在动载作用下的破坏失稳进行分析，其静载下的力学模型如图1所示，动静组合加载下的力学模型如图2所示。

图1 静载下煤岩组合系统的力学模型Fig.1 The mechanics model of compound coal-rock under static loading

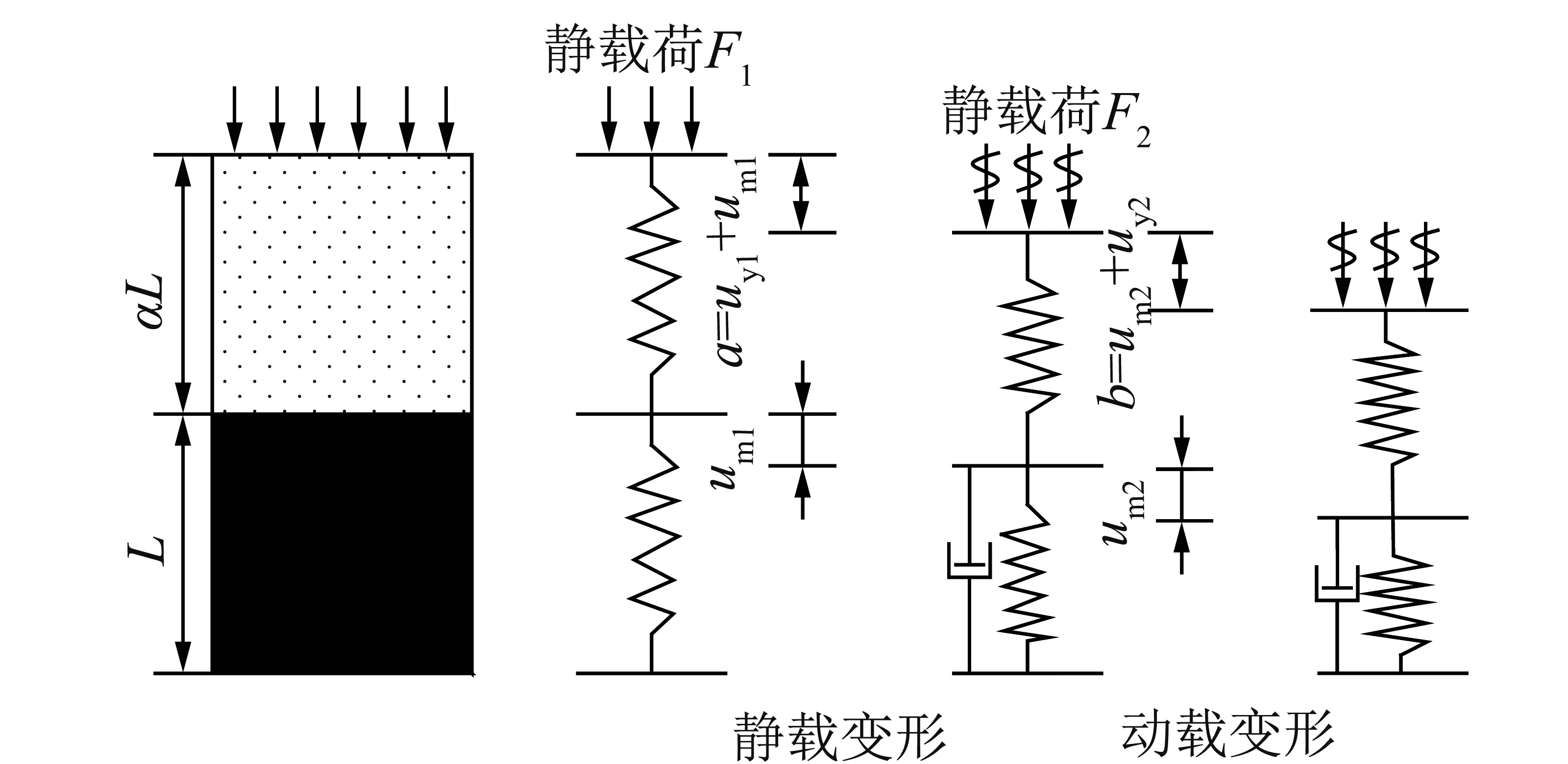
图2 动静载下煤岩组合系统的力学模型Fig.2 The mechanics model of compound coal-rock under coupled static and dynamic loading

1.1 一维静载下的煤岩组合系统分析

如图1所示，F1为对煤岩组合施加的轴向一维静载。煤岩组合系统中，煤样的长度为L，岩样的长度为αL，截面面积均为S，静载F1下煤的变形为um1，岩石的变形为uy1，煤岩组合系统整体变形为a=um1+uy1。

对于处于弹性变形状态的岩石，静载载荷F1与岩石的变形uy1之间的关系为

(1)

其中，k1为静载下岩石的刚度。

煤自身含有较多裂隙，需要考虑其损伤特性，即煤的本构关系是具有弱化性质的非线性关系，因此静载载荷F1与um1之间的关系[24]为

(2)

式中,λ1=E1S/L为煤样的初始刚度，E1为静载下煤的弹性模量;u0为完整度，具有长度量纲，为单轴加载下峰值载荷所对应的变形值。

则静载下系统的势函数V1即是它具有的总能量：

(3)

将uy1=a-um1代入式(3)并积分得

(4)

1.2 一维动静加载下的煤岩组合系统分析

动静加载下的煤岩组合系统如图2所示，在轴向一维静载F1的基础上加入与之同方向的动载荷F2的扰动。此时岩石依然看作弹性体，而煤在动静共同作用下变形、屈服到破坏期间，不仅表现出损伤特性，还有黏性，如下：

(5)

其中，m为Weibull分布中分布曲线的形状系数；η为煤的黏性系数；ε00一般位于峰值应力对应的应变与平均应变之间[24]。

设动载下煤的变形为um2，岩石的变形为uy2，煤岩组合系统整体变形为b=um2+uy2，动载荷F2和动载下煤的变形um2的关系如下:

(6)

此时动载下系统的势函数V2为

(7)

(8)

由式(8)可得奇点集为

gradum2(gradum2VZ)=

(9)

根据平衡曲面的光滑性质，在尖点处有：

(10)

即：

(11)

所以在尖点处：

(12)

即

(13)

(14)

其中：

(15)

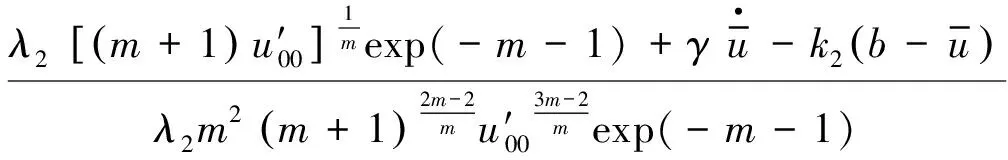
(16)

这里K为动静载下煤和岩石的刚度比，k2为动静载下岩石的刚度；A0，B0，C0均只与形状系数m有关。

1.3 结果分析

对于式(14)只有在P≤0时成立，即在P≤0时煤岩组合系统能跨越分歧点集，因此由式(15)得系统发生突变的必要条件是：

(17)

将λ2=E2S/L，k2=EYS/αL代入式(17)中，其中,EY为动静载下岩石的弹性模量，式(17)变为

(18)

式(18)即为动静加载下煤岩组合系统发生突变失稳的判据，由此表明岩石和煤的高度比越大、岩石弹模和动静加载下煤的初始弹模的比值越小，动静加载下煤岩组合系统越容易发生突变失稳。该结果说明了顶板和煤层的厚度比越大、顶板弹模和动静加载下煤层的初始弹模的比值越小，井下的煤岩体结构在动载扰动下越容易发生突变失稳。

接下来，推导煤岩组合系统发生突跳时的位移变化量。由以上的分析可以知道当P≤0时，系统才可能发生突跳。此时平衡方程(14)有3个实根，分别为

(19)

(20)

跨越分岔点集时的状态变量的无量纲突跳位移为

(21)

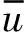
(22)

其中：

引入无量纲能量UZ：

(23)

所以，突变前后的能量差为

ΔUZ=UZ(x1)-UZ(x2)=

(24)

将式(19),(20)代入式(24)得到失稳破坏时释放的无量纲能量ΔUZ为

(26)

由式(21),(25)可知，动静载下煤岩组合系统失稳破坏的突跳位移与释放总能量均与岩石和煤的高度比、岩石弹模和动静加载下煤的初始弹性模量的比值、煤的厚度以及形状系数m有关。突跳位移与岩石和煤的高度比正相关，与岩石弹性模量和动静加载下煤的初始弹性模量的比值、煤的厚度负相关；而系统失稳所释放的总能量却与岩石和煤的高度比、煤的厚度负相关，与岩石弹性模量和动静加载下煤的初始弹性模量的比值正相关。该结果说明了井下煤岩体结构在动载扰动下发生突变失稳的位移与顶板和煤层的厚度比正相关、顶板弹性模量和动静加载下煤层的初始弹性模量的比值以及煤层厚度负相关。而失稳的剧烈程度是顶板和煤层的厚度比、煤层厚度负相关，与顶板弹性模量和动静加载下煤层的初始弹性模量的比值正相关。

综上，由于岩石和煤在动静加载下的弹性模量是由外部载荷和静载下的弹性模量共同决定的[25-27]，从而可知静载下煤岩自身性质和动静载荷是煤岩组合系统在的动静加载下破坏失稳的判据、剧烈程度以及突跳位移的主要影响因素。并且可知动载扰动下井下煤岩体结构发生突变失稳的条件、位移以及剧烈程度受顶板和煤层的厚度比、顶板弹性模量和动静加载下煤层的初始弹性模量的比值以及煤层厚度的影响规律。

2 动静载下煤岩组合系统破坏失稳的混沌机制

通过建立非线性动力学模型，来描述动静加载下煤岩组合系统的演化过程，从而揭示其演化过程中的混沌机制。

(27)

在煤岩组合系统动态失稳过程中，受到的非平衡合力，还可由式(22)求出：

(28)

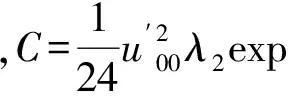
由式(27),(28)得到：

(29)

方程(29)两边同除以m变为

(30)

杜芬方程的标准形式相比，式(30)多了一个常数项B，这是由于组合系统受到了静载的作用而导致的，可以用B表征组合煤岩所受静载。为了便于问题分析，式(30)的系数取u′=0.3，C′=1，C′P=-1，ω=1.2[28]：

(31)

动静加载下组合煤岩破坏失稳是个复杂的物理过程，这里将其看作以下两部分的耦合来加以解释，包括组合煤岩自身的非线性系统和外部动静载荷构成的简谐震荡系统：

图3 煤岩组合系统参数x随着的变化的分岔Fig.3 The bifurcation diagram of compound rock-coal between x and subjected to different B value

综上可知，动静加载下煤岩组合系统的演化过程随着动载振幅的增大呈现阶段性，其原因是外载能量与系统自身的固有能量之间的相互影响，说明动载振幅对于动静加载下组合煤岩的演化过程起着决定性作用。当组合煤岩自身的非线性作用与外部动静载荷作用相当时，组合煤岩的演化过程进入混沌阶段。我们知道，动载诱发冲击地压的发生是动静组合加载下煤岩体结构的破坏失稳；通过上述的研究，可以推断井下煤岩体结构与动静载荷之间的相互作用是影响冲击地压从孕育至启动的整个演化过程的关键。并且动载诱发冲击地压的演化过程是有序阶段和混沌阶段的复杂集合，从而对动载诱发冲击地压进行准确的预测预报是比较困难的。

图4 不同B时煤岩组合系统进入混沌状态的临界Fig.4 The threshold of compound rock-coal into chaos subjected to different B value

3 一维动静加载下组合煤岩破坏失稳试验分析

3.1 试验设备及样品

为了对以上得到的一维动静载下组合煤岩的失稳判据(式(18))和释放的总能量(式(26))进行验证，特在中南大学进行的改进霍普金森杆试验。煤岩样的概况见表1，试样图片如图5所示。

试验中施加动载的种类是与静载同方向的半周期正弦波。改进后的霍普金森杆的结构示意图如图6所示[30]。本试验采用的霍普金森压杆，入射波的加载时间是定值，大约均为200 μs，变化的是应力波的幅值。

表1煤岩样参数
Table1Theparametersofcoalandrockmodels

试样物理力学性质单轴抗压强度/MPa煤取自新疆宽沟煤矿，埋深316m的块状煤体。沥青光泽，阶梯状断口，含少许层状夹矸。属于半亮型煤，坚硬，裂隙垂直发育28 8岩石取自新疆宽沟煤矿顶板岩石，埋深316m的粗砂岩。坚硬、均质、内生裂隙不发育93 7煤岩组合试样35 0

图5 试验所用试样Fig.5 The models in the experiment

图6 改进的霍普金森杆的构造Fig.6 Configuration of improved SHPB device

每个试样端面和圆周都进行仔细研磨，两端不平行度小于0.02 mm，圆周与端面的不垂直度小于0.02 mm。组合系统为高60 mm，直径50 mm的圆柱体。煤和岩石的高度比为1∶1，煤、岩之间使用乳胶黏合。纯煤试样为高30 mm，直径50 mm的圆柱体。

3.2 试验方法

首先，需要通过对试验得到应力应变曲线进行分析以及试算分析，对u00,m，EY，E2，ΔVZ这5个参数进行确定(各参数含义参照第2节)。其中，u00，m，ΔVZ是通过煤岩组合系统的动静加载试验获得，而E2是通过对纯煤的动静加载试验获得，2个试验所施加的动、静载值基本一致。

从试验结果来看，动静加载下组合煤岩的应变率小于110 s-1，则同样的动静载荷施加在纯岩石的试样上应变率必然要更小。已有的试验结果表明，当应变率小于102s-1时，强度大于90 MPa的岩石的物理力学指标与静载几乎相同[27]，而本试验所采用的岩石单轴强度为93.7 MPa，因此，EY选用由煤炭科学研究总院开采分院岩石力学实验室测定的静载下岩石弹模，为31.65 GPa。

采用正交试验设计，第1组试验保持静载不变，变换动载的大小；第2组试验保持动载不变，变换静载的大小。分别得到各个应力加载情况下的参数值。首先，静载为18 MPa不变，动载幅值是从使试样破坏的最小动载开始选取，其幅值分别为140，190，240，290 MPa。然后，动载幅值为140 MPa不变，静载分别为0，5，18，26 MPa。通过粘贴在入射杆和反射杆上的应变片对入射、反射、透射波进行采集。

3.3 试验结果及分析

图7是动静载下纯煤的应力应变曲线，通过曲线可以计算出煤在不同动静加载下的初始弹性模量(图中框内曲线的斜率)，计算结果为表2中的E2。由表2可知，动静加载下煤的初始弹性模量E2随动载幅值A2的增大而增大，但受静载F1的影响较小。

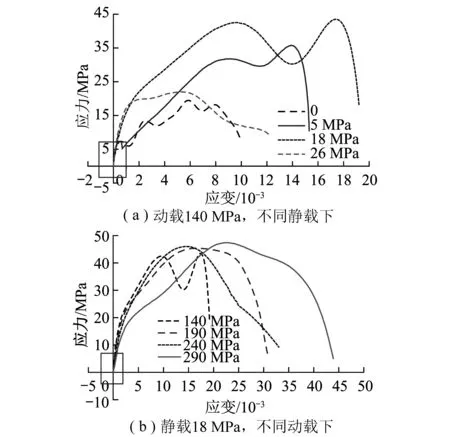
图7 纯煤的应力应变曲线Fig.7 The stress-strain curves of coal

并且从表2可以看出，动载幅值在140～190 MPa范围内，煤岩组合系统动静载下发生破坏时均为K≤M，初步证明了式(32)中动静加载下的失稳判据是合理的。并且通过式(26)得到动静载下组合煤岩破坏失稳时释放总能量的理论值与试验值基本一致，误差小于10%。但更大范围的动载幅值对动静加载下煤岩组合系统破坏失稳的影响有待进一步试验。

表2动静组合加载试验的各项参数
Table2Theparametersofcoupledstaticanddynamicloadsexperiment

F1/MPaA2/MPaEY/GPaE2/GPamu00/108αKMΔVZ理论值试验值误差/%1814031 651391 5428 0010 2280 2307 327 877 01819031 651411 5858 0010 2240 24417 4417 082 11824031 651471 6468 0010 2160 26453 6252 262 61829031 651781 7438 0010 1780 29867 9167 101 2014031 651441 5788 0010 2200 24113 5013 202 2514031 651401 6008 0010 2260 24925 6125 301 22614031 651401 5402 5010 2260 2293 313 184 4

4 结 论

(1)得到了一维动静载下煤岩组合系统的破坏判据、突跳位移及释放总能量的数学表达式，由此可知动载扰动下井下煤岩体结构发生突变失稳的条件、位移以及剧烈程度受顶板和煤层的厚度比、顶板弹性模量和动静加载下煤层的初始弹性模量的比值以及煤层厚度的影响规律；最后对理论结果进行试验验证，表明理论值和试验值吻合较好。

(2)建立了一维动静加载下组合煤岩的非线性动力学模型，发现了外载能量与系统自身固有能量之间的相互作用导致模型的演化过程呈阶段性并出现混沌现象。由此推断出煤岩体结构与动静载荷之间的相互作用是影响动载诱发冲击地压演化过程的关键。

(3)当组合系统本身的非线性作用与外部载荷的作用能力相当时，系统演化进入混沌阶段。由此推断出动载诱发冲击地压的演化过程同样是有序阶段和混沌阶段的复杂集合，从而对这类冲击地压进行准确的预测预报是比较困难的。

(4)动载振幅对于一维动静加载下组合煤岩的演化过程起着决定性作用，而静载的增大使得系统有序性有所提高。

(5)当其它系统参数确定时，关键静载下的组合煤岩受到较小的动载扰动就会进入混沌状态。

[1] 齐庆新，窦林名.冲击地压理论与技术[M].北京:中国矿业大学出版社，2008.

[2] 齐庆新，史元伟，刘天泉.冲击地压粘滑失稳机理的试验研究[J].煤炭学报，1997，22(2)：144-148. Qi Qingxin,Shi Yuanwei,Liu Tianquan.Mechanism of instability caused by viscous sliding in rock burst[J].Journal of China Coal Sciety,1997,22(2):144-148.

[3] 齐庆新.层状煤岩体结构破坏的冲击矿压理论与实践研究[D].北京：煤炭科学研究总院，1996. Qi Qingxin.The study on its theory and pratice of rockburst led by the structure failure of bedded coal-rock mass[D].Beijing:China Coal Research Institute，1996.

[4] 李纪青，齐庆新，毛德兵,等.应用煤岩组合模型方法评价煤岩冲击倾向性探讨[J].岩石力学与工程学报，2005，24：4805-4810. Li Jiqing,Qi Qingxin,Mao Debing,et al.Discussion on evaluation method of bursting liability with compsite model of coal and rock[J].Chinese Journal of Rock Mechanics and Engineering,2005,24:4805-4810.

[5] 姜耀东，王 涛，宋义敏,等.煤岩组合结构失稳滑动过程的试验研究[J].煤炭学报，2013，38(2)：177-182. Jiang Yaodong,Wang Tao,Song Yimin,et al.Experimental study on the stick-slip process of coal-rock composite samples[J].Journal of China Coal Sciety,2013,38(2):177-182.

[6] 赵毅鑫，姜耀东，祝 捷,等.煤岩组合体变形破坏前兆信息的试验研究[J].岩石力学与工程学报，2008，27(2)：339-346. Zhao Yixin，Jiang Yaodong，Zhu Jie,et al.Experimental study on precursory information of deformations of coal-rock composite samples before failure[J].Chinese Journal of Rock Mechanics and Engineering,2008,27(2):339-346.

[7] 郭东明，左建平，张 毅,等.不同倾角组合煤岩体的强度与破坏机制研究[J].岩土力学，2011，32(5):1333-1339. Guo Dongming,Zuo Jianping,Zhang Yi,et al.Research on strength and failure mechanism of deep coal-rock combination bodies of different inclined angles[J].Rock and Soil Mechanics,2011,32(5):1333-1339.

[8] 窦林名，陆菜平，牟宗龙,等.组合煤岩冲击倾向性特性试验研究[J].采矿与安全工程学报，2006，23(1)：43-46. Dou Linming,Lu Caiping,Mu Zonglong,et al.Rockburst tendency of coal-rock combinations sample[J].Journal of Mining & Safety Engineering,2006，23(1):43-46.

[9] 左建平，谢和平，吴爱民,等.深部煤岩单体及组合体的破坏机制与力学特性研究[J].岩石力学与工程学报，2011，30(1):84-92. Zuo Jianping,Xie Heping,Wu Aimin,et al.Investigation on failure mechanisms and mechanical behaviors of deep coal-rock body and combined body[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(1):84-92.

[10] 窦林名，赵从国,杨思光,等.煤矿开采冲击矿压灾害防治[M].徐州:中国矿业大学出版社，2006.

[11] 姜耀东，赵毅鑫，刘文岗,等.煤岩冲击失稳的机理和试验研究[M].北京:科学出版社，2009.

[12] 潘俊锋，宁 宇，杜涛涛,等.区域大范围防范冲击地压的理论与体系[J].煤炭学报，2012，37(11):1803-1809. Pan Junfeng,Ning Yu,Du Taotao,et al.The theory and system for preventing rock burst in large-scale areas[J].Journal of China Coal Sciety,2012,37(11):1803-1809.

[13] 蓝 航，杜涛涛，彭永伟,等.浅埋深回采工作面冲击地压发生机理及防治[J].煤炭学报，2012，37(10):1618-1623. Lan Hang,Du Taotao,Peng Yongwei,et al.Rock-burst mechanism and prevention in working face of shallow buried coal-seam[J].Journal of China Coal Sciety,2012,37(10):1618-1623.

[14] 潘 岳，王志强,张 勇.突变理论在岩体系统动力失稳中的应用[M].北京:科学出版社，2008.

[15] Zhu W C,Bai Y,Li X B,et al.Numerical simulation on rock failure under combined static and dynamic loading during SHPB tests[J].International Journal of Impact Engineering,2012,49:142-157.

[16] Li Xibing,Zhou Zilong,Zhao Fujun,et al.Mechanical properties of rock under coupled static-dynamic loads[J].Journal of Rock Mechanics and Geotechnical Engineering,2009,1(1):41-47.

[17] 刘少虹，李凤明，蓝 航，等.动静加载下煤的破坏特性及机理的试验研究[J].岩石力学与工程学报，2013，32(S2)：3749-3759. Liu Shaohong,Li Fengming,Lan Hang,et al.Experimental study of failure characteristics and mechanism of coal under coupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Engineering,2013,32(S2):3749-3759.

[18] 左宇军，李夕兵，马德春,等.动静组合载荷作用下岩石失稳破坏的突变理论模型与实验研究[J].岩石力学与工程学报，2005，24(5):741-746. Zuo Yujun,Li Xibing,Ma Dechun,et al.Catastrophic model and testing study on failure of static loading rock system under dynamic loading[J].Chinese Journal of Rock Mechanics and Engineering，2005，24(5):741-746.

[19] 于亚伦.岩石动力学[R].北京:北京科技大学，1990.

[20] 郑永来，夏颂佑.岩石粘弹性连续损伤本构模型[J].岩石力学与工程学报，1996，15(S1)：428-432. Zheng Yonglai,Xia Songyou.Viscoelastic damage constitutive model for rock[J].Chinese Journal of Rock Mechanics and Engineering,1996,15(S1):428-432.

[21] 胡柳青.冲击载荷作用下岩石动态断裂的机理研究[D].长沙:中南大学，2005. Hu Liuqing.On the mechanism of the dynamic fracture poreesses of rock under impulse loading[D].Changsha:Central South University,2005.

[22] 单仁亮，薛友松，张 倩.岩石动态破坏的时效损伤本构模型[J].岩石力学与工程学报，2003，22(11):1771-1776. Shan Renliang,Xue Yousong,Zhang Qian.Time dependent damage model of rock[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(11):1771-1776.

[23] 李夕兵，左宇军，马春德.中应变率下动静组合加载岩石的本构模型[J].岩石力学与工程学报，2005，25(5):865-874. Li Xibing,Zuo Yujun,Ma Chunde.Constitutive model of rock under coupled static-dynamic loading with intermediate strain rate[J].Chinese Journal of Rock Mechanics and Engineering,2005,25(5):865-874.

[24] 唐春安.岩石破裂过程中的灾变[M].北京:煤炭工业出版社，1993. Tang Chun’an.Catastrophe in rock unstable failure[M].Beijing:China Coal Industry Publishing House,1993.

[25] 杨桂通.弹塑性动力学基础[M].北京:科学出版社，2008.

[26] 宫凤强，李夕兵，刘希灵,等.一维动静组合加载下砂岩动力学特性的试验研究[J].岩石力学与工程学报，2010，29(10):2076-2085. Gong Fengqiang,Li Xibing,Liu Xiling,et al.Experimental study of dynamic characteristics of sandstone under one-dimensional coupled static and dynamic loads[J].Chinese Journal of Rock Mechanics and Engineering,2010,29(10):2076-2085.

[27] 李夕兵，古德生.岩石冲击动力学[M].长沙:中南大学出版社，1994.

[28] 秦四清.斜坡失稳的突变模型与混沌机制[J].岩石力学与工程学报，2000，19(4):486-492. Qin Siqing.Nonlinear catastrophy model of slope instability and chaotic dynamic mechanism of slope ecolution process[J].Chinese Journal of Geotechnical Engineering,2000,19(4):486-492.

[29] Grebogi C，Ott E Crises，sudden changes in chaotic attractors and transient chaos[J].Physics，1983,7D:181-200.

[30] Yin Zhiqiang，Li Xibing，Jin Jiefang,et al.Failure characteristics of high stress rock induced by la disturbance under confining pressure unloading[J].Trans.Nonferrous Met.Soc.China，2012(22):175-184.

Nonlinearcatastrophymodelandchaoticdynamicmechanismofcompoundcoal-rockunstablefailureundercoupledstatic-dynamicloading

LIU Shao-hong1,2

(1.CoalMiningandDesigningBranch，ChinaCoalResearchInstitute，Beijing100013，China；2.CoalMiningandDesigningDepartment，TiandiScienceandTechnologyCo.，Ltd.，Beijing100013，China)

In order to deepen understanding the mechanism of rockburst induced by dynamic loading,the judgement formula of failure,catatrophic displacement and the total released energy of compound coal-rock under coupled static-dynamic loading were obtained by time dependent damage model and catastrophe theory.And,nonlinear dynamic model of compound coal-rock under coupled static-dynamic loading was established.Based on this,author found that the interaction of loading energy and system inheret energy lead that the model evolution exhibits stepwise and chaotic characteristic.When the roles of the nonlinear system itself and of the external loads are the same,the system begin to enter the chaotic evolution stage.It follows that the interaction between the mine coal-rock structure and the coupled static and dynamic loadings is the key of the evolution of dynamic rockburst.At last,the experiments of coupled dynamic and static loadings vertified the theoretical results,and it shows that the theoretical analysis are in good agreement with the experimental values.

coupled static-dynamic loading;compound coal-rock system;catastrophe theory;chaos theory;rockburst

10.13225/j.cnki.jccs.2013.2007

国家重点基础研究发展计划(973)资助项目(2010CB226806)；国家科技支撑计划资助项目(2012BAK09B01)

刘少虹(1982—)，男，辽宁鞍山人，博士，工程师。E-mail：liushaohong@tdkcsj.com

TD324

A

0253-9993(2014)02-0292-09

刘少虹.动静加载下组合煤岩破坏失稳的突变模型和混沌机制[J].煤炭学报,2014,39(2):292-300.

Liu Shaohong.Nonlinear catastrophy model and chaotic dynamic mechanism of compound coal-rock unstable failure under coupled static-dynamic loading[J].Journal of China Coal Society,2014,39(2):292-300.doi:10.13225/j.cnki.jccs.2013.2007