基于颗粒流理论的煤岩冲击倾向性细观模拟试验研究
2014-09-11赵同彬尹延春谭云亮邹建超
赵同彬,尹延春,谭云亮,魏 平,邹建超
(1.山东科技大学 矿山灾害预防控制-省部共建教育部重点实验室培育基地,山东 青岛 266590;2.山东科技大学 矿业与安全工程学院,山东 青岛 266590;3.中国矿业大学(北京) 资源与安全工程学院,北京 100083)
基于颗粒流理论的煤岩冲击倾向性细观模拟试验研究
赵同彬1,2,3,尹延春1,2,谭云亮1,2,魏 平2,邹建超2
(1.山东科技大学 矿山灾害预防控制-省部共建教育部重点实验室培育基地,山东 青岛 266590;2.山东科技大学 矿业与安全工程学院,山东 青岛 266590;3.中国矿业大学(北京) 资源与安全工程学院,北京 100083)
为了研究煤岩不同细观参数均质度对冲击倾向性的影响,利用细观颗粒流软件模拟了弹性模量和黏结强度分别服从Weibull分布的非均质煤岩,并通过进行单轴压缩试验分析了破坏过程中的能量积聚与释放,研究了不同均质度m的煤岩冲击倾向性。分析表明:颗粒弹性模量均质度m与宏观弹性模量之间呈幂函数关系,m越大,峰前积聚的能量越多,冲击倾向性越明显;颗粒间黏结强度均质度m与宏观抗压强度之间呈幂函数关系,m越大,峰前积聚的能量越多,煤岩破坏由塑性向脆性转化,峰后能量释放速度加快,冲击倾向性越明显;黏结强度均质性影响峰前的能量积聚和峰后的能量释放,而弹性模量均质性只影响峰前的能量积聚,黏结强度均质性对冲击倾向性的影响大于弹性模量,起主导作用。
颗粒流;煤岩冲击倾向性;细观非均质
岩石是一种典型的多孔介质,由多种大小、形状各不相同的矿物晶体组成,并由一定的胶结物黏结在一起。岩石在细观层次上其结构是非常不均匀的,是一种天然的非均质材料,其细观组成特性影响着岩石的物理力学性质、强度等宏观力学行为[1-3]。在岩石失稳破裂过程中,其非均质性影响着裂纹的生成及扩展,决定着岩石破坏的最终形态,因此研究岩石非均质性对其宏观力学行为的影响规律,有助于进一步研究岩石材料的冲击倾向性、破裂规律、应变局部化等热点问题,具有重要的学术价值和工程意义[4-6]。关于岩石非均匀性,谢和平等[7]利用概率统计和分形几何方法,研究了脆性材料结构中的裂纹分布规律,认为岩石的不均匀特性可以用Weibull分布来表示。在此种假设基础上,很多学者对岩石的非均质特性进行了大量的研究[8-9]。王士民等[10]假定脆性材料的非均匀性符合Weibull分布,研究了坡度参数对岩石破坏形式的影响。梁正召等[11]利用RFPA进行了非均匀岩石的单轴压缩试验,分析了细观结构非均匀性对岩石损伤软化过程和宏观力学性能的影响。冯增朝等[12]研究了非均质岩石的全程应力应变曲线,揭示出冲击倾向性指标E/λ与非均质参数m之间遵循负指数关系。
本文在假定煤岩细观参数服从Weibull分布的基础上,利用颗粒流软件模拟了不同弹性模量和黏结强度均质度的煤岩宏观力学性能,并通过进行单轴压缩试验分析了煤岩破坏过程中能量的积聚和释放,研究了均质性对冲击倾向性的影响。
1 煤岩非均质颗粒流模型
1.1 颗粒流简介
煤岩是由矿物颗粒组成的,因此采用颗粒流程序能很好的模拟其细观特征,从本质上反映煤岩的宏观力学行为,是一种可以从细观层次研究力学问题的有效方法[13-14]。在颗粒流程序中,颗粒单元为圆形刚性体,之间的接触为柔性接触,并且存在黏结。颗粒流的黏结模型包括接触黏结模型和平行黏结模型,接触黏结表示颗粒之间点的黏结,常用于模拟散体材料,如土体;平行黏结模型表示颗粒之间面的黏结,常用于模拟密实材料,如煤岩。本文模拟选用的模型为平行黏结模型,该模型细观参数设定包括颗粒弹性模量和颗粒之间的黏结强度,可以分别设定2种参数的均质度,来分析其对冲击倾向性的影响。
1.2 煤岩非均质模拟
Weibull分布是现阶段非均质研究中应用最广泛的细观参数设定方法,其概率分布函数P(x)和概率密度函数f(x)如下:
(1)
(2)
式中,x0表示期望值;m表示均质度。
图1为期望值x0为1时的不同m的概率密度函数曲线,通过曲线可知,均质度m越大,煤岩细观参数离散性越小,整体性质越均匀。
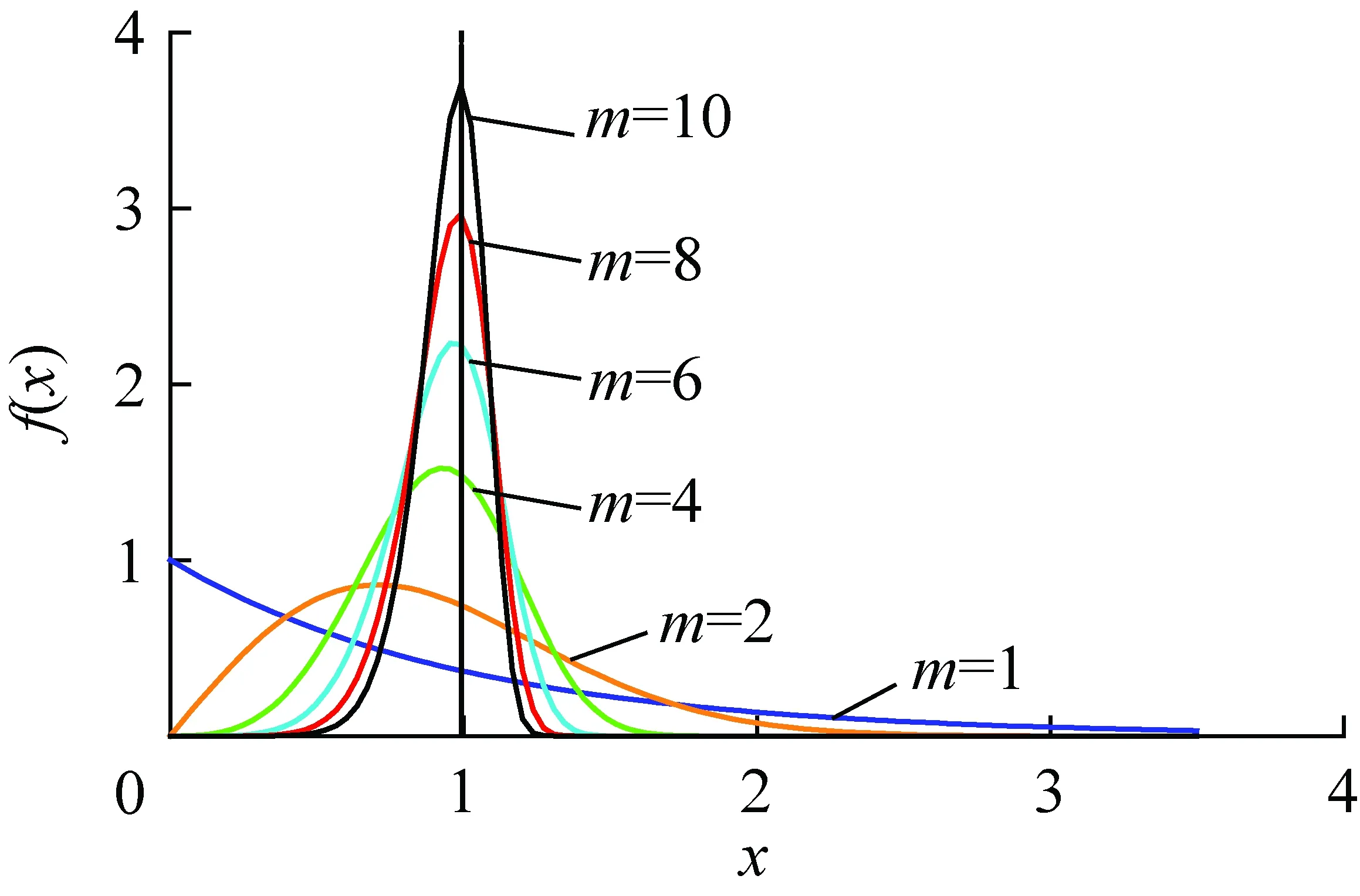
图1 Weibull分布概率密度曲线Fig.1 Curve of probability density of Weibull distribution
为了分析颗粒弹性模量均质度与黏结强度均质度对冲击倾向性的不同影响,设计了2种方案。一种是黏结强度保持不变,改变颗粒弹性模量的均质度,期望值E0=10 GPa;另一种是颗粒弹性模量保持不变,改变黏结强度的均质度,期望值σ0=50 MPa。模型的其他细观参数设定为:颗粒半径0.2~0.3 mm,密度1 800 kg/m3,黏结半径1,摩擦因数0.1。
模型尺寸为标准试件50 mm×100 mm,为了防止颗粒溢出,墙体要加长。为了保证在区域内生成足够的颗粒来满足孔隙率,采用半径扩展法生成模型,先将颗粒半径缩小,生成颗粒,然后根据孔隙率将半径扩展。半径扩展后,颗粒间会出现不平衡力,通过循环消除不平衡力,使颗粒达到平衡状态,基本模型生成。然后对模型参数赋值,循环一定步数后消除不平衡力。模型生成后,通过移动顶部墙体来给试样施加荷载,加载速度为0.01 mm/s。在计算过程中可以通过编写fish函数记录加载过程中的变形能变化过程,进而分析能量的积聚和释放。试件加载模型如图2所示,图中不同颜色的颗粒根据Weibull函数分别赋予不同的细观参数。

图2 单轴压缩试验模型Fig.2 Model of uniaxial compressing test
1.3 煤岩冲击倾向性指标
煤岩所具有的积蓄变形能并产生冲击式破坏的性质,可用一个或几个指数来衡量。根据中华人民共和国国家标准《煤的冲击倾向性分类及指数的测定方法GB/T 25217.2—2010》,煤岩的冲击倾向性指数包括动态破坏时间DT、弹性能量指数WET、冲击能量指数KE、单轴抗压强度RC。本文采用冲击能量指数作为判定冲击倾向性的标准,冲击能量指数是指试件在单轴压缩状态下,应力应变全过程曲线中峰值前积蓄的变形能与峰值后耗损的变形能之比,计算方法为式(3)。冲击倾向性的判定标准见表1。
(3)
式中,As为试件峰前积聚的变形能;Ax为峰后消耗的变形能。
表1煤岩冲击倾向性标准
Table1Criterionofbursttrend

类别1类2类3类冲击倾向无弱强冲击能量指数KE<1 51 5≤KE<5 0KE≥5 0
2 均质度对冲击倾向性的影响
2.1 颗粒弹性模量均质度的影响
图3为得到的煤岩不同颗粒弹性模量均质度mE的应力-应变曲线,图4为宏观弹性模量E随均质度的变化曲线。通过分析曲线可知,颗粒弹性模量均质度对单轴抗压强度影响很小,随着均质度的增大,宏观弹性模量增大,并且增大幅度逐渐减小,均质度mE与宏观弹性模量大体呈幂函数关系:
(4)
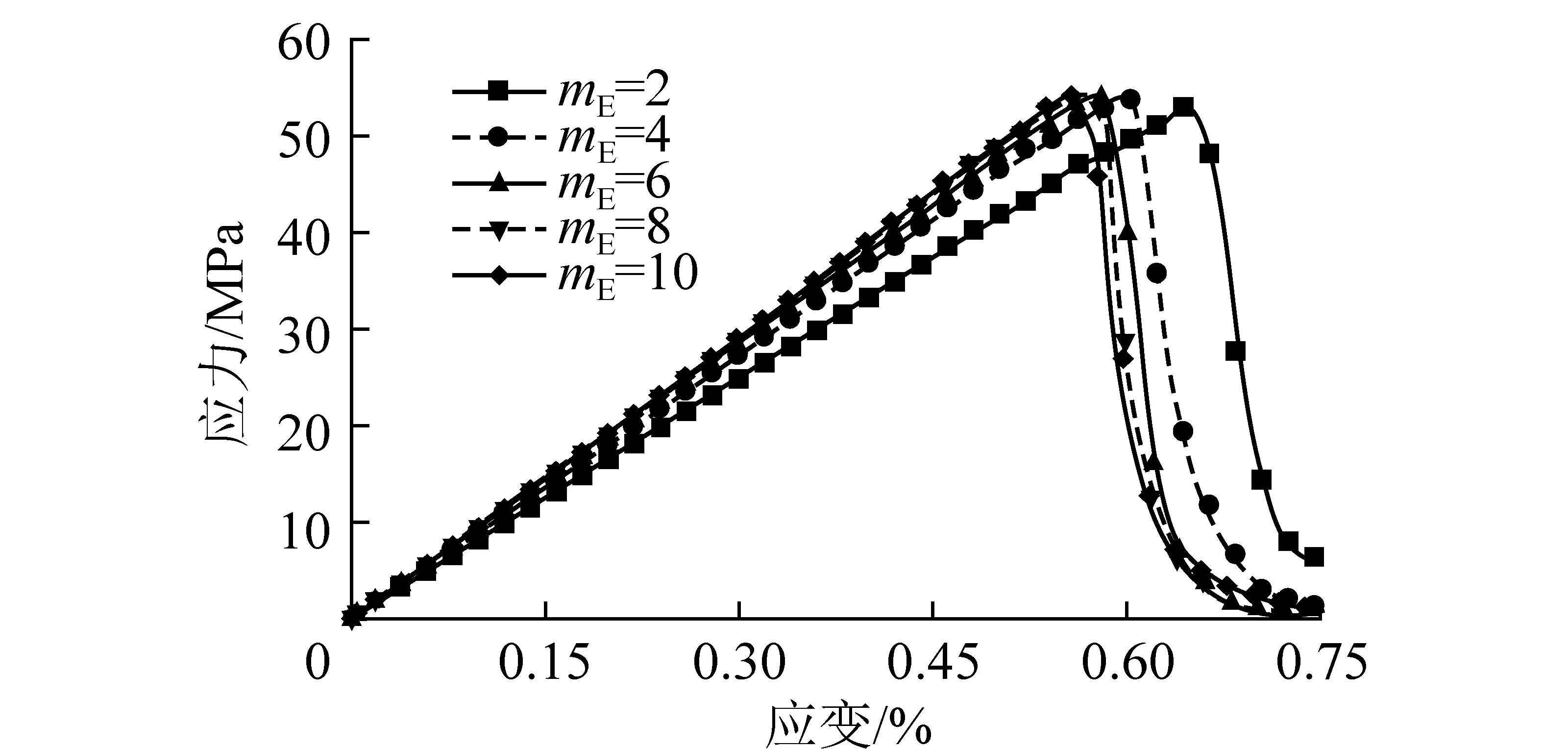
图3 不同弹性模量均质度的应力-应变曲线Fig.3 Stress-strain curves with heterogeneous modulus
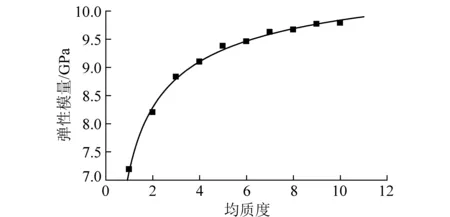
图4 弹性模量与均质度的关系曲线Fig.4 Curve of elastic modulus and heterogeneity
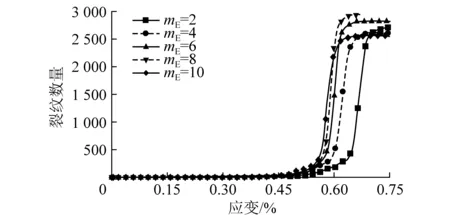
图5 不同弹性模量均质度的裂纹曲线Fig.5 Crack curves with heterogeneous modulus
图5为得到的不同弹性模量均质度mE煤岩加载过程中裂纹数量变化曲线。由于各颗粒之间黏结强度一样,各模型在相同时刻产生裂纹。当均质度较小时,颗粒单元之间的弹性模量差距较大,煤岩偏软,压力施加速度较慢,试件裂纹生成演化时间较长,而均质度mE较大的试件裂纹生成演化时间较短。由于黏结强度分布均匀,因此对最终裂纹的生成数量影响较小。
图6为得到的不同弹性模量均质度煤岩加载过程中变形能变化曲线。在均质度较小时,煤岩破坏前积聚的能量较少,随着均质度的增大,能量积聚逐渐增多,而均质度对峰后能量的释放影响很小。

图6 不同弹性模量均质度的变形能曲线Fig.6 Energy curves with heterogeneous modulus
图7为冲击能量指数随均质度的变化曲线,随着弹性模量均质度的增大,煤岩的冲击能量指数不断增大,冲击倾向性越明显。

图7 冲击能量指数与弹性模量均质度的关系曲线Fig.7 Curve of impact energy index and heterogeneity
当弹性模量均质度mE较小时,颗粒之间的弹性模量差距较大,煤岩偏软,压力施加速度较慢,在加载过程中能量缓慢积聚,当局部应力超过颗粒间的黏结强度后,黏结破坏,生成裂纹,积聚的能量得到释放,由于裂纹的生成扩展时间较长,能量释放比较充分,煤岩在峰前积聚的能量较小,冲击倾向性较弱。当弹性模量均质度mE较大时,颗粒之间的弹性模量差距较小,能量积聚过程较快,破坏前释放的能量较少,煤岩在峰前积聚的能量较大,冲击倾向性较强。
2.2 颗粒黏结强度均质度的影响
图8为得到的煤岩不同颗粒间黏结强度均质度mσ的应力-应变曲线,图9为抗压强度σ随黏结强度均质度的变化曲线。通过分析曲线可知,颗粒间黏结强度的均质度对宏观弹性模量几乎没有影响,随着均质度的增大,煤岩的单轴抗压强度逐渐增大,并且增加幅度逐渐减小,两者之间大体呈幂函数关系,关系式为公式(5)。通过分析应力应变曲线的峰后变化可知,随着黏结强度均质度的增大,煤岩的破坏由塑性向脆性变化。
(5)
图10为得到的不同黏结强度均质度mσ时煤岩加载过程中裂纹数量变化曲线。在均质度mσ较小时,试件中低强度的黏结数量较多,在很小的压力下试件就开始产生裂纹,并且扩展演化时间较长,产生的裂纹数量较多;随着mσ的增大,裂纹生成时刻延后,并且扩展时间逐渐变短,在较少的数量下煤岩就已完全破坏。

图8 不同黏结强度均质度的应力-应变曲线Fig.8 Stress-strain curves with heterogeneous strength
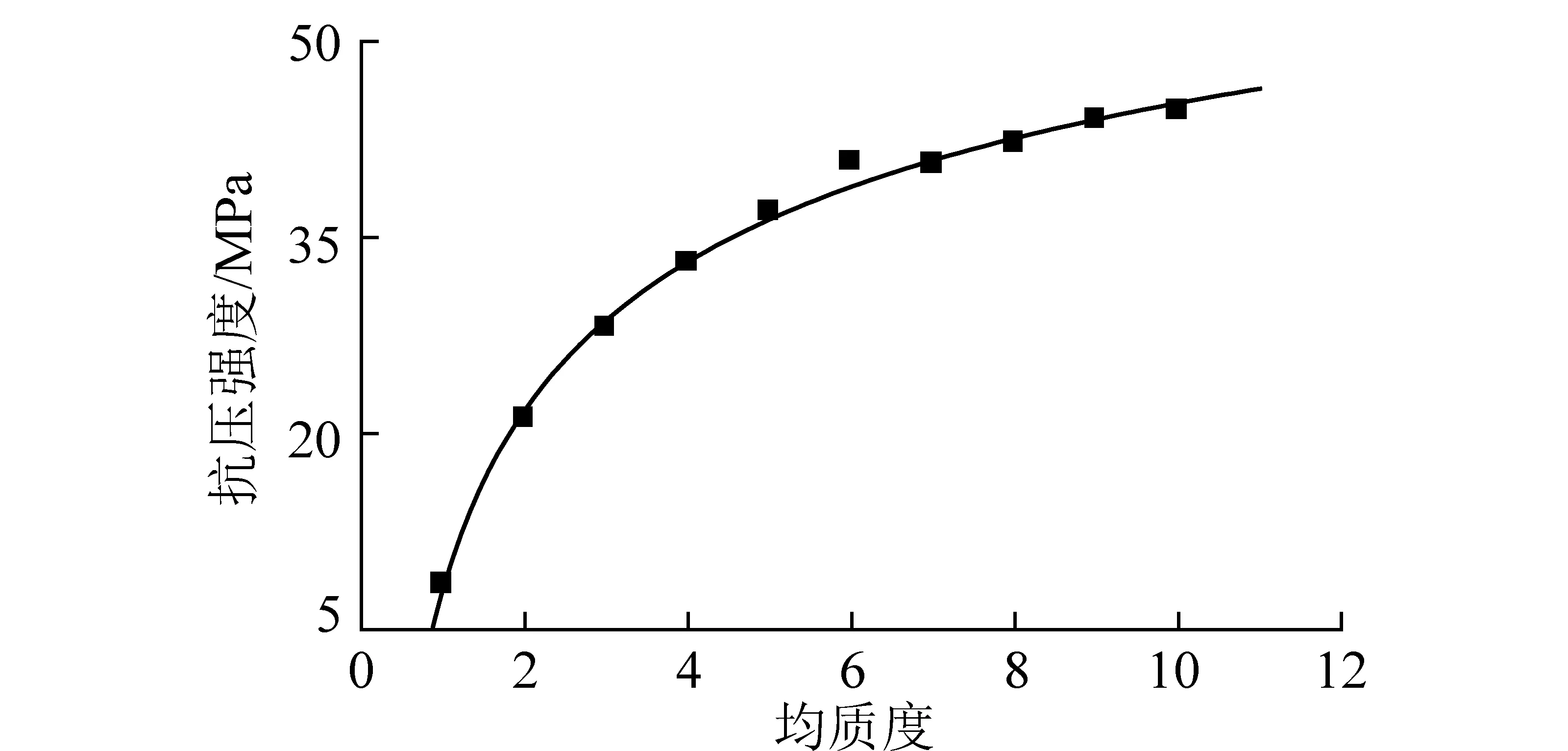
图9 抗压强度与均质度的关系曲线Fig.9 Curve of heterogeneity and compressive strength
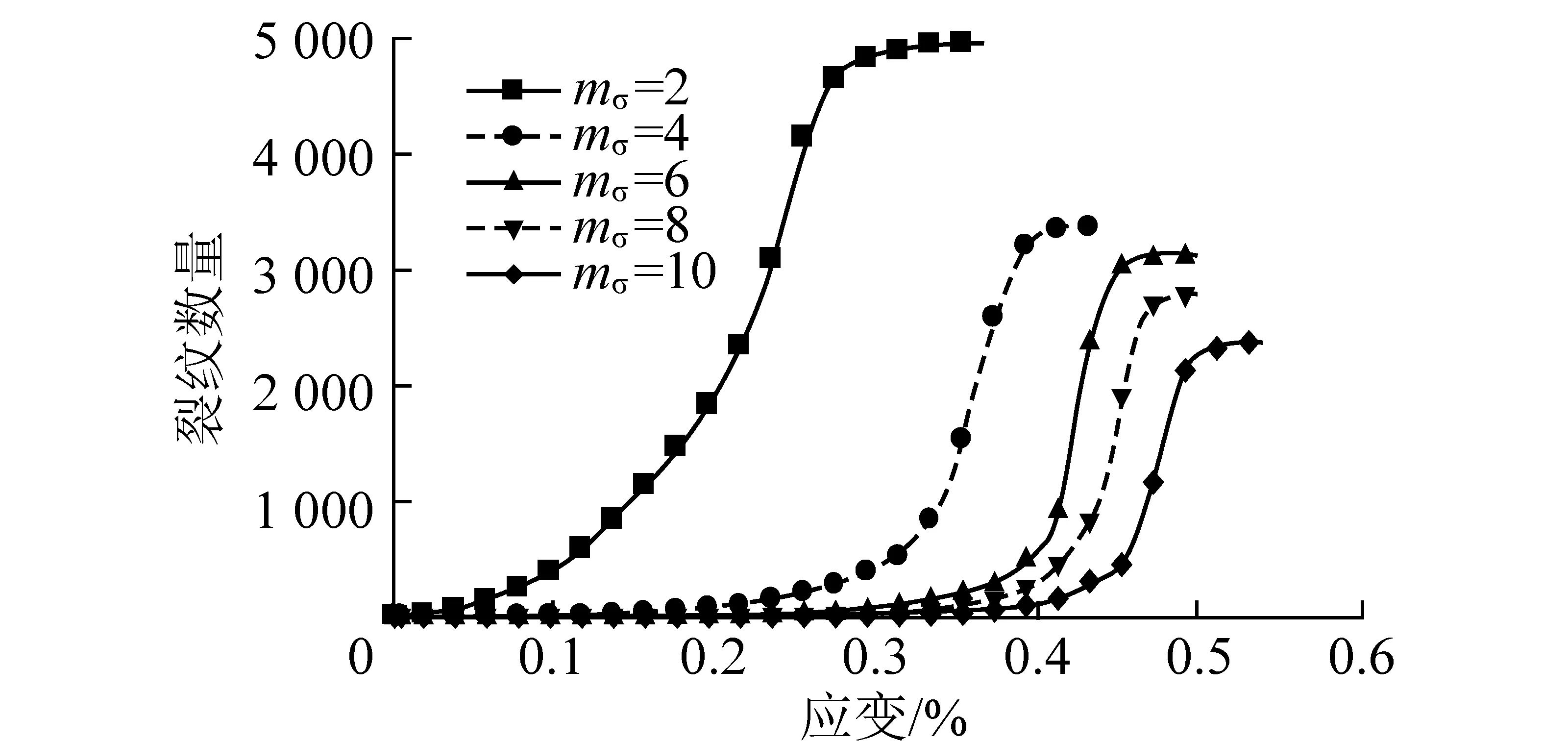
图10 不同黏结强度均质度的裂纹曲线Fig.10 Crack curves with heterogeneous strength
图11为不同黏结强度均质度mσ的煤岩破坏形态,在均质度很小时,在模型表面随机分布着大量的微小裂隙,试件整体零散裂纹较多,随着均质度的增大,裂隙分布局部化现象越来越明显,逐渐向破裂带附近积聚。

图11 不同黏结强度均质度的试件破坏形态Fig.11 Failure modes with heterogeneous strength
图12为得到的不同黏结强度均质度mσ试件加载过程中变形能变化曲线。均质度较小时,峰前试件积聚的能量较小,而且峰后能量缓慢释放,冲击倾向性较弱。均质度较大时,峰前积聚的能量较大,而且峰后能量瞬间释放,易发生冲击现象。

图12 不同黏结强度均质度的变形能曲线Fig.12 Energy curves with heterogeneous strength
图13为冲击能量指数随黏结强度均质度mσ的变化曲线,随着均质度的增大,煤岩的冲击能量指数不断增大,冲击倾向性越明显。

图13 冲击能量指数与黏结强度均质度的关系曲线Fig.13 Curve of impact energy index and heterogeneity
当煤岩黏结强度均质度mσ较小时,颗粒之间的黏结强度差距较大,在很低的压力下,黏结开始破坏,并且贯穿整个加载过程,因此在加载过程中积聚的能量不断消耗,在峰前能量积聚量较小。由于黏结强度差距较大,局部裂纹扩展是不连续的,因此煤岩具有明显的屈服阶段,达到极限破坏强度后,煤岩缓慢破坏,峰后能量释放较慢。由于峰前积聚能量较小,峰后能量缓慢释放,因此均质度较小的煤岩冲击倾向性较弱,不易发生冲击现象。当黏结强度均质度mσ较大时,极限破坏强度较大,峰前积聚的能量较多。而且由于黏结强度之间差距较小,当黏结开始破坏时,将产生连锁效应,裂纹持续生成扩展,煤岩将在极短的时间内破坏,峰后能量释放迅速。由于峰前积聚能量较大,峰后能量释放迅速,因此均质度较大的煤岩冲击倾向性较强,易发生冲击现象。
2.3 均质度参数影响的比较探讨
通过对比颗粒弹性模量均质度与颗粒间黏结强度均质度对冲击倾向性的影响可知:弹性模量均质度对冲击能量指数的影响变化范围为4.64~6.15,而黏结强度均质度对冲击能量指数的影响变化范围为1.53~6.31,黏结强度均质度对冲击倾向性的影响程度大于弹性模量,起主导作用。弹性模量是煤岩的弹性变形参数,该参数对煤岩弹性阶段的变形影响较大,而对塑性变形及峰后破坏的影响较小,只影响破坏前的能量积聚。而黏结强度对峰前和峰后的变形破坏情况都有影响,决定着峰前的能量积聚和峰后的能量释放过程,因此黏结强度均质度对冲击倾向性的影响较大。
3 结 论
(1)颗粒流程序中的平行黏结模型可以很好地模拟煤岩材料,该模型参数设定中包括颗粒弹性模量和黏结强度,可以分别实现2种不同参数的均质度,进而分析其对宏观力学性质的影响。
(2)颗粒弹性模量的均质度对单轴抗压强度的影响很小,与宏观弹性模量呈幂函数关系。随着均质度的增大,煤岩均质性越好,破坏前积聚的能量增加,冲击倾向性越明显,发生冲击的几率越大。
(3)颗粒间黏结强度的均质度对宏观弹性模量的影响很小,与抗压强度呈幂函数关系。随着均质度的增大,煤岩均质性越好,破坏前积聚的能量增加,而且由于破坏由塑性向脆性转化,峰后能量释放速度加快,因此均质度较大的煤岩具有明显的冲击倾向性,易发生冲击现象。
(4)弹性模量均质度只影响煤岩破坏前的能量积聚,而黏结强度均质度对破坏前的能量积聚和破坏后的能量释放都有影响,黏结强度均质度对冲击倾向性的影响远远大于弹性模量,起主导作用。
[1] 罗 荣,曾亚武,杜 欣.非均质岩石材料细观力学参数的关系研究[J].岩土工程学报,2012,34(12):2331-2336. Luo Rong,Zeng Yawu,Du Xin.Relationship between macroscopic and mesoscopic mechanical parameters of inhomogeneous rock material[J].Chinese Journal of Geotechnical Engineering,2012,34(12):2331-2336.
[2] 张春会.非均匀、随机裂隙展布岩体渗流应力耦合模型[J].煤炭学报,2009,34(11):1460-1464. Zhang Chunhui.Seepage-stress coupled model of heterogeneous and random fractured rockmass[J].Journal of China Coal Society,2009,34(11):1460-1464.
[3] 赵同彬,谭云亮,张 泽.大台井深部水平岩爆的地质力学机理分析[J].煤炭学报,2010,35(12):2039-2044. Zhao Tongbin,Tan Yunliang,Zhang Ze.Geomechanical mechanism of rock burst in deep level of Datai Mine[J].Journal of China Coal Society,2010,35(12):2039-2044.
[4] 朱泽奇,肖培伟,盛 谦,等.基于数字图像处理的非均质岩石材料破坏过程模拟[J].岩土力学,2011,32(12):3780-3786. Zhu Zeqi,Xiao Peiwei,Sheng Qian,et al.Numerical simulation of fracture propagation of heterogeneous rock material based on digital image processing[J].Rock and Soil Mechanics,2011,32(12):3780-3786.
[5] Yun S C,Harrison J P.A review of the state of the art in modeling progressive mechanical breakdown and associated fluid flow in intact heterogeneous rocks[J].International Journal of Rock Mechanics and Mining Sciences,2006,43(7):1001-1022.
[6] 宿 辉,党承华,李彦军.考虑不均质度的岩石声发射数值模拟研究[J].岩土力学,2011,32(6):1886-1890. Su Hui,Dang Chenghua,Li Yanjun.Study of numerical simulation of acoustic emission in rock of inhomogeneity[J].Rock and Soil Mechanics,2011,32(6):1886-1890.
[7] 高 峰,谢和平.脆性材料的分形统计强度理论[J].固体力学学报,1996,17(3):239-244. Gao Feng,Xie Heping.Fractal statistics strength theory of fragile material[J].Acta Mechanica Solida Sinica,1996,17(3):239-244.
[8] 吕兆兴,冯增朝,赵阳升.岩石的非均质性对其材料强度尺寸效应的影响[J].煤炭学报,2007,32(9):917-920. Lü Zhaoxing,Feng Zengchao,Zhao Yangsheng.Influence of rock inhomogeneity on strength-size effect of rock materials[J].Journal of China Coal Society,2007,32(9):917-920.
[9] 赵 瑜,李晓红,卢义玉,等.瓦斯压力对非均质煤岩抗压强度尺寸效应的影响[J].煤炭学报,2009,34(8):1081-1085. Zhao Yu,Li Xiaohong,Lu Yiyu,et al.Influence of gas pressure on compressive strength size effect of inhomogeneous coal[J].Journal of China Coal Society,2009,34(8):1081-1085.
[10] 王士民,朱合华,冯夏庭,等.细观非均匀性对脆性岩石材料宏观破坏形式的影响[J].岩土力学,2006,27(2):224-227. Wang Shimin,Zhu Hehua,Feng Xiating,et al.Influence of heterogeneity on macroscopical crack form of the brittle rock[J].Rock and Soil Mechanics,2006,27(2):224-227.
[11] 梁正召,杨天鸿,唐春安,等.非均匀性岩石破坏过程的三维损伤软化模型与数值模拟[J].岩土工程学报,2005,27(12):1447-1452. Liang Zhengzhao,Yang Tianhong,Tang Chun’an,et al.Three-dimensional damage soften model for failure process of heterogeneous rocks and associated numerical simulation[J].Chinese Journal of Geotechnical Engineering,2005,27(12):1447-1452.
[12] 冯增朝,赵阳升.岩石非均质性与冲击倾向的相关规律研究[J].岩石力学与工程学报,2003,22(11):1863-1865. Feng Zengchao,Zhao Yangsheng.Correlativity of rock inhomogeneity and rock burst trend[J].Chinese Journal of Rock Mechanics and Engineering,2003,22(11):1863-1865.
[13] 赵同彬,尹延春,谭云亮,等.锚杆界面力学试验及剪应力传递规律细观模拟分析[J].采矿与安全工程学报,2011,28(2):220-224. Zhao Tongbin,Yin Yanchun,Tan Yunliang,et al.Mechanical test of bolt interface and microscopic simulation of transfer law for shear stress[J].Journal of Mining & Safety Engineering,2011,28(2):220-224.
[14] 尹延春,赵同彬,谭云亮,等.锚固体应力分布演化规律及其影响因素研究[J].采矿与安全工程学报,2013,30(5):712-716. Yin Yanchun,Zhao Tongbin,Tan Yunliang,et al.Research of stress distribution evolution law and influencing factors[J].Journal of Mining & Safety Engineering,2013,30(5):712-716.
Burstingliabilityofcoalresearchofheterogeneouscoalbasedonparticleflowmicroscopictest
ZHAO Tong-bin1,2,3,YIN Yan-chun1,2,TAN Yun-liang1,2,WEI Ping2,ZOU Jian-chao2
(1.StateKeyLaboratoryBreedingBaseforMiningDisasterPreventionandControl,ShandongUniversityofScienceandTechnology,Qingdao266590,China;2.CollegeofMiningandSafetyEngineering,ShandongUniversityofScienceandTechnology,Qingdao266590,China;3.FacultyofResourcesandSafetyEngineering,ChinaUniversityofMiningandTechnology(Beijing),Beijing100083,China)
To research the influence of different heterogeneous parameters on bursting liability of coal,the uniaxial compressing tests of heterogeneous coal based on Weibull distribution with different elastic modulus and bonding strength were simulated by using particle flow code(PFC).The accumulation and release of energy was studied,and bursting liability of coal with different heterogeneities was researched.The results indicate that the elastic modulus heterogeneity has a power function relation with macroscopic modulus.With the increase of the modulus heterogeneity,more energy is accumulated before peak strength.The bursting liability of coal is more possible at high modulus heterogeneity.The bond strength heterogeneity has a power function relation with compressive strength.With the increase of the strength heterogeneity,more energy is accumulated before peak strength,and the energy release speeds up after peak.The coal failure type transforms from plastic to fragility.The bursting liability of coal is more possible at high strength heterogeneity.The bond strength heterogeneity with influence on before and after peak strength has more impact on bursting liability of coal compared with modulus heterogeneity with influence only on before peak.
particle flow;bursting liability of coal;microscopic heterogeneity
10.13225/j.cnki.jccs.2013.2017

国家重点基础研究发展计划(973)资助项目(2010CB226805);教育部高等学校博士学科点专项科研基金资助项目(20123718110013);山东省“泰山学者”建设工程专项经费资助项目
赵同彬(1975—),男,黑龙江齐齐哈尔人,博士,副教授。通讯作者:尹延春(1988—),男,山东济南人,博士研究生。E-mail:yycrsd@163.com
TD324
A
0253-9993(2014)02-0280-06
赵同彬,尹延春,谭云亮,等.基于颗粒流理论的煤岩冲击倾向性细观模拟试验研究[J].煤炭学报,2014,39(2):280-285.
Zhao Tongbin,Yin Yanchun,Tan Yunliang,et al.Bursting liability of coal research of heterogeneous coal based on particle flow microscopic test[J].Journal of China Coal Society,2014,39(2):280-285.doi:10.13225/j.cnki.jccs.2013.2017
