一种基于沉积模式的多点地质统计学建模方法

尹艳树，张昌民，李少华，王军，宋道万，龚蔚青

1）长江大学地球科学学院，湖北荆州，434023；2）胜利油田地质科学研究院，山东东营，257015

内容提要：地下储层分布是位置的函数，不同位置处的沉积模式具有差异性。在储层预测时，除了挖掘已有资料所提供的结构和统计信息外，还应该引入待估点位置的信息，以反映沉积储层模式随位置变化的非平稳特征。提出了一种基于沉积模式的多点地质统计学方法，通过距离函数将储层特征与沉积位置相关联，采用整体替换、结构化随机路径以及多重网格策略再现沉积模式。基于现代鄱阳湖沉积所建立的合成非平稳性三角洲前缘沉积地层建模表明，新设计的方法较传统的建模方法更好地反映了三角洲相沉积地层非平稳沉积模式，新设计方法有更好的地质适用性。研究丰富了储层三维建模理论和方法，为实际油藏建模提供了新手段。

1 问题的提出

储层预测是指根据周围条件数据点对待估点储层特征的一种估计。不同估计方法和手段构成不同的建模方法。在预测时，强调对已知信息的挖掘，以约束和指导待估点的预测。对信息的挖掘包括两个方面，一是挖掘数据所反映的储层空间结构特征，二是揭示数据所反映的储层统计特征。在两点地质统计中，储层空间结构通过变差函数进行描述（侯加根，1993；彭仕宓等，2004；马晓强等，2012）；在多点统计中，储层结构通过空间多点联合来反映（吴胜和等，2005；尹艳树等，2006）。但无论两点统计还是多点统计，其推断前提是空间数据结构满足平稳性假设，从而可将周围条件信息节点作为同一个随机变量对待。

基于对河流相储层平稳性的广泛认可（Deutsch and Journel，1998），以及河流储层的简单性，很多建模方法都是在河流储层中完成测试和检验，并推广到其他沉积储层的。例如，多点地质统计学建模方法（尹艳树等，2008a；Strebelle and Journel，2001；Strebelle，2002；Liu Yuhong et al.，2004；Ezequiel and González，2008；Caers and Zhang Tuanfeng，2004；Arpat and Caers，2007）主要在河流相储层中展开。正因为建模对象符合平稳性假设，其建模效果都较好，得以在油田中推广。

随着研究深入，在非河流相储层建模时，两点和多点统计建模效果引起争议，其适应性开始广为关注。特别是在扇相储层和三角洲相储层，分支河道方位和规模在远离物源方向上不断变化特征难以获得再现（图1）。不少学者对此进行了建模方法的改进，如变方位角模拟（Strebelle，2007）、平稳变换模拟（Manuel and Carrera，2009）、分区模拟（Roy and Strebelle，2008）等，取得了一定效果。但实际沉积储层研究中，分支河道方位变化性信息很难获得，导致平稳变换很难实施；分区模拟则具有主观任意性。导致扇相储层和三角洲相储层模拟仍然需要进一步深入研究。

从数学地质角度看，储层沉积模式随距离变化性正是储层非平稳性的典型反映。传统的两点统计和多点统计的数学基础是平稳性假设，导致其在非平稳性储层建模上适应性差。对于我国陆相储层，储层分布具有多样性和复杂非均质性，扇相储层和三角洲相储层是重要油气储层和开发重点对象。加强储层地质建模研究，提高建模准确度，对于油气储层表征、剩余油预测和挖潜具有重要意义。

2 方法原理

图1 多点统计不能再现扇体储层空间分布（据Caers and Zhang Tuanfeng，2002）Fig.1 The simulation result of fan reservoir with multiple point geostatistics（after Caers and Zhang Tuanfeng，2002）

地下储层是时间与空间函数，表现在平面上随位置、垂向上随时间储层变化特征。从时空变化性可以看出，储层在任一位置都是具有特定的沉积模式。如果将沉积储层特征随位置的变化性加以考虑，则有望解决储层非平稳性建模的问题。基于这样的考虑，在建模时将储层空间位置引入到储层预测中，更好再现储层沉积模式。

对于待估点，其位置坐标为（xu，yu，zu），构建一个待估点与训练图像位置之间的距离函数：

其中，（xu，yu，zu）为待估点处坐标，（xT，yT，zT）为训练图像处数据事件中心点处坐标。

距离函数描述了待估点在训练图像中的相对位置。由于沉积特征是随位置而变化的，待估点的相对位置实际上揭示了可能的沉积模式。例如，如果待估点相对位置靠近训练图像中物源位置，则发育补给水道的可能性较大，水道窄而深，宽厚比小；如果远离物源方向，则为分支水道沉积的可能性大，水道宽而浅，宽厚比大。对应的，在主补给水道位置，可能以水道与天然堤组合的特征；而在远离物源位置，则有可能是侧向拼接分支水道模式。

条件数据的存在为进一步明确沉积模式提供了更多的证据。在待估点处，周围条件数据构成某个特定的数据事件。此时，以待估点处条件数据组成数据事件扫描训练图像，确定在训练图像中与之匹配的数据事件。同样地，距离函数被应用于此处：

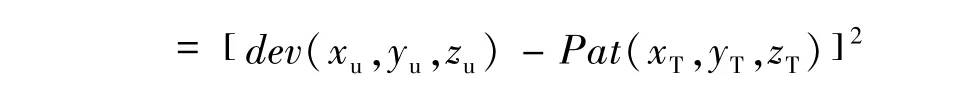
其中dev（xu，yu，zu）为待估点周围条件数据事件，Pat（xT，yT，zT）为训练图像中数据事件值。

通过计算待估点位置距离值，以及待估点周围数据事件与训练图像数据事件之间的距离值，就可以建立一个总的距离函数：

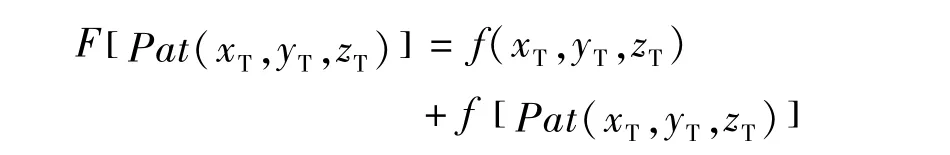
在实际储层预测时，选择训练图像中总距离最小的数据事件Pat（xT，yT，zT）作为模拟最终结果。

通过图2可以进一步描述方法的原理，以及与传统方法的差异。阐明在储层预测中沉积位置、条件数据与沉积模式预测之间的内在联系。

在图2中，左侧是训练图像，右侧上方是待估点位置及周围条件数据。如果仅考虑条件数据，则在训练图像中存在3个满足条件的数据事件（a，b，c）。但3个数据事件分别位于三角洲前缘不同部位，代表了不同沉积模式。在传统的建模方法中，通过随机抽样来决定待估点处数据事件。显然，选择不同数据事件将会导致不同的模拟结果。模拟结果所揭示的沉积储层模式很可能与训练图像中沉积模式有较大差异。新设计的方法则提取了待估点的位置信息作为约束，计算其与训练图像中满足条件的数据事件中心点位置距离。由于沉积模式是位置的函数，因此选择距离最小的数据事件（数据事件c）作为最终模拟结果，有效地将训练图像沉积模式和特征复制到待估区域，模拟沉积储层结构与训练图像具有更好的一致性。同时由于其忠实于条件数据信息，模拟结果具有更高的可信度。

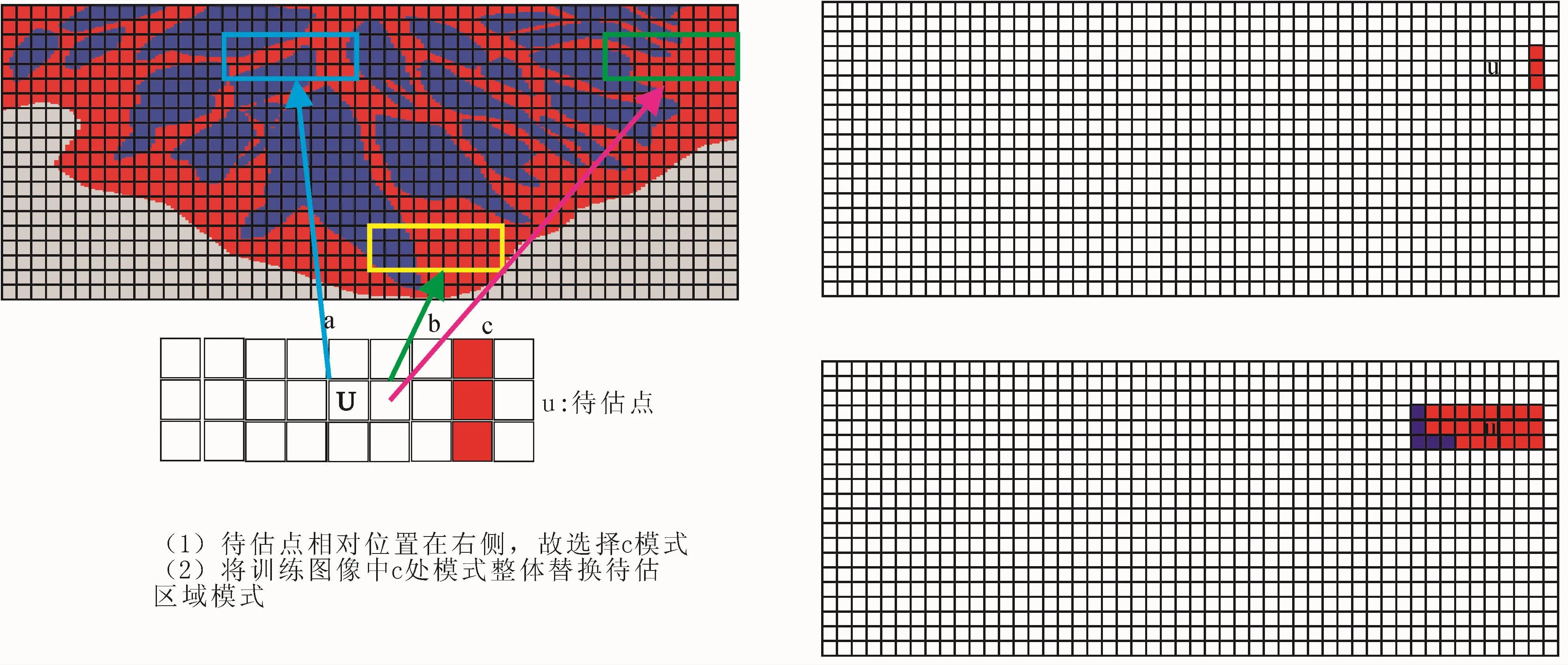
图2 沉积位置以及条件数据对储层预测的影响Fig.2 The effection of the deposit place and conditional data to the selection of sediment pattern

需要指出的是，对沉积相而言，其代码没有进行归一化处理，而模拟又需要满足已有条件数据匹配，数据事件距离函数最小实质是在训练图像中的数据事件完全满足待估点处条件数据。在待估点周围条件数据太多的时候，数据事件之间可能存在不匹配。此时需要舍弃部分条件数据，考察条件数据的信息度，将信息度最小的条件节点逐一舍弃，直到达到完全匹配（尹艳树等，2008b）。另外一种情况是满足待估点条件的数据事件数量较少，代表奇异的沉积模式。同样的，需要舍弃信息度最小条件节点，以满足统计意义上的合理性。

在待估点周围没有条件数据时，位置距离函数成为了唯一选择标准。但储层沉积多变性表明井间预测具有不确定性。为了描述这种不确定性，设置一个位置距离容差半径（Rd），训练图像中在此范围内的数据事件均可能作为待估点处沉积模式。此种可能性通过蒙特卡罗抽样来进行唯一确定。

最后，为了体现储层非均质性的层次性，采用了多重网格方式进行建模（Tran，1994），以反映不同层次和规模储层非均质性特征。而为了更好地利用条件数据约束建模，采用半随机的结构化路径方法（Liu Yuhong and Journel，2004），先模拟条件数据多的待估点，然后逐渐扩展到条件数据较少区域。

综上，模拟基本步骤如下：

（1）数据预处理，建立研究区训练图像。训练图像描述了研究区的位置信息，以及相对位置处沉积模式。

（2）模拟参数设置，确定搜索数据样板大小，以及模拟所需要的最小重复数据事件个数。

（3）根据条件数据分布，确定半随机的结构化路径。

图3 距离容差内随机数据事件选择示意Fig.3 The random seletion of data event in the defined distance tolerance

（4）对结构化路径上的待估点，以其周围条件数据组成的数据事件为条件，扫描训练图像，找出与待估点周围条件数据相匹配的所有数据事件及数据事件所在位置。

（5）通过距离函数计算训练图像中满足条件的数据事件位置与待估点位置之间的距离，选择距离最小的数据事件作为模拟结果。

（6）利用满足条件的训练图像中的数据事件整体替换待估点处数据事件。

（7）模拟转入下一个待估点，重复（4）～（6）步骤，直到所有网格节点模拟完成。

3 方法检验

作为新方法设计的初衷，再现非平稳沉积储层特征是其最终目的。以鄱阳湖现代沉积非平稳性地层为例，通过一个合成的三维训练图像，对方法进行了检验。

鄱阳湖发育较为典型的现代浅水分流砂坝型沉积地层（张昌民等，2010）。在河流向湖心方向上，河流受地形、水流动力等影响，河流携带砂体堆积在河口形成分流砂坝，河道在分流砂坝的作用下产生分叉，并在前方继续沉积分流砂坝，形成喇叭形分流砂坝型沉积地层（图4）。自入湖口向湖心方向，河道能量逐渐减弱，河道沉积厚度变薄，宽厚比增加，河道密度增加，河道流向变化范围大；分流砂坝则逐渐增多，其走向与河道一致，变化性大。表现为典型的非平稳地质特征。

图4 现代鄱阳湖沉积模式（据张昌民等，2010）Fig.4 The sedimentary pattern of Poyang Lake，China（after Zhang changmin et al.，2010）

采用Petrel数字化功能，将鄱阳湖部分区域数字化作为训练图像。并根据沉积机理赋予了其三维地质意义，建立了一个合成的三维训练图像（图5）。训练图像网格密度为199×199×10。以此训练图像作为参考，开展算法的检验。

图5合成的鄱阳湖三维训练图像Fig.5 A synthesized 3-D training image of Poyang Lake

图6 是利用Petrel软件自带的多点地质统计学方法进行的建模。数据样板规模是10×10×3，采用二重网格策略。从建立的地质模型看，分流河道分叉性以及流向的变化性在模型中没有得到反映，分流砂坝与分流河道空间配置关系也不太明显。所建立的模型没有反应分流砂坝型三角洲特有的沉积模式。为了保证算法检验对比的一致性，在新设计方法中也采用相同的数据样板和网格策略。

图7是利用新设计方法建立的地质模型。从图7可以看出，三角洲前缘沉积储层整体呈扇形分布特征。在分流砂坝影响下，分流河道分叉性得到了很好再现。自河口向湖心方向，河道分叉增多，分流砂坝比例增加。分流河道与分流砂坝空间配置也得到了准确反映。此外，三角洲前缘与前三角洲的分界特征也得到非常准确的反应。所建立的地质模型与现代鄱阳湖沉积非常接近。表明新设计的方法能够再现储层非平稳地质特征，精细刻画了三角洲前缘储层沉积模式。

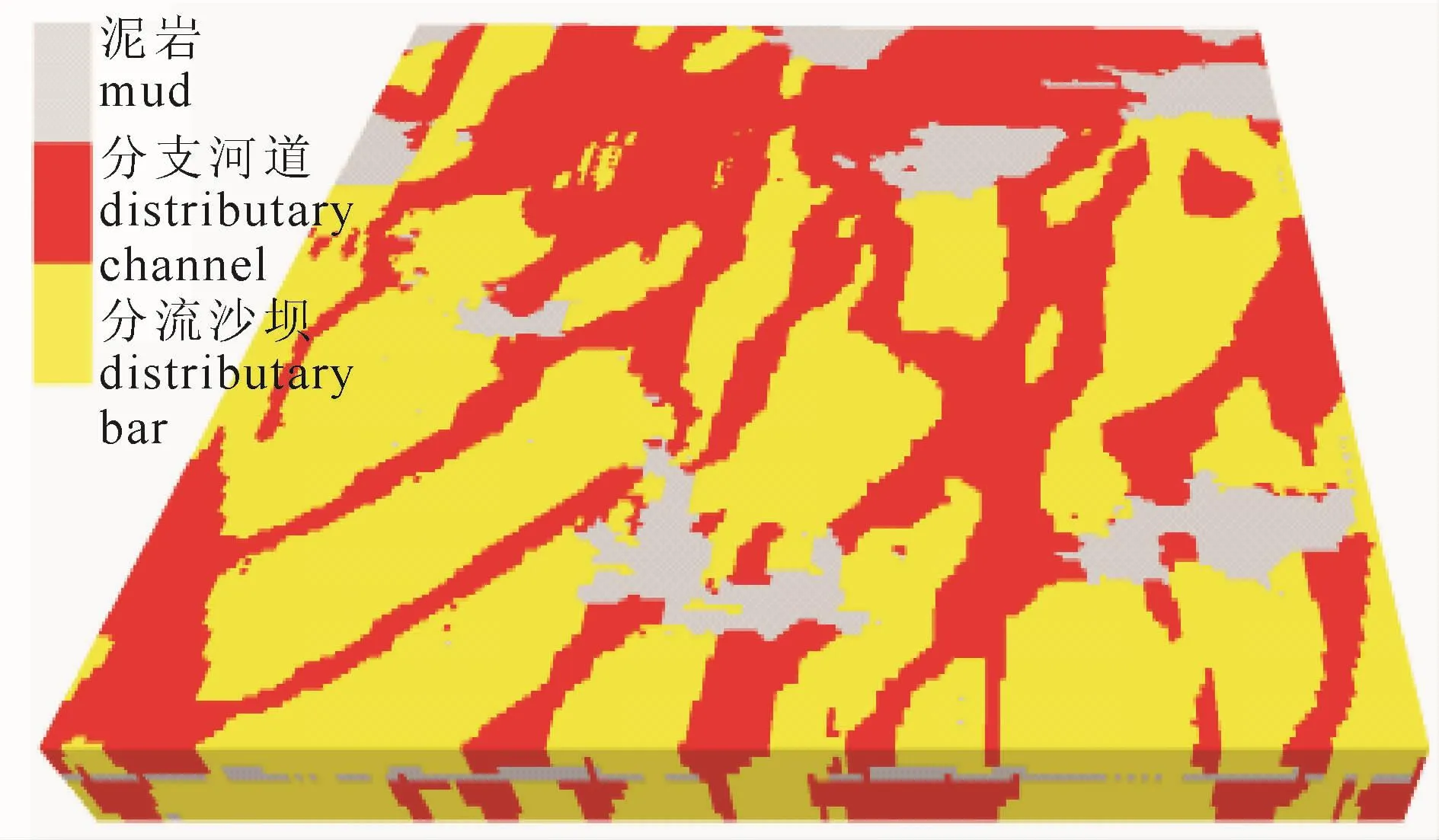
图6 Petrel软件中多点模块建立的鄱阳湖储层地质模型Fig.6 The model of Poyang Lake constructed by multiple point geostatistics in Petrel software

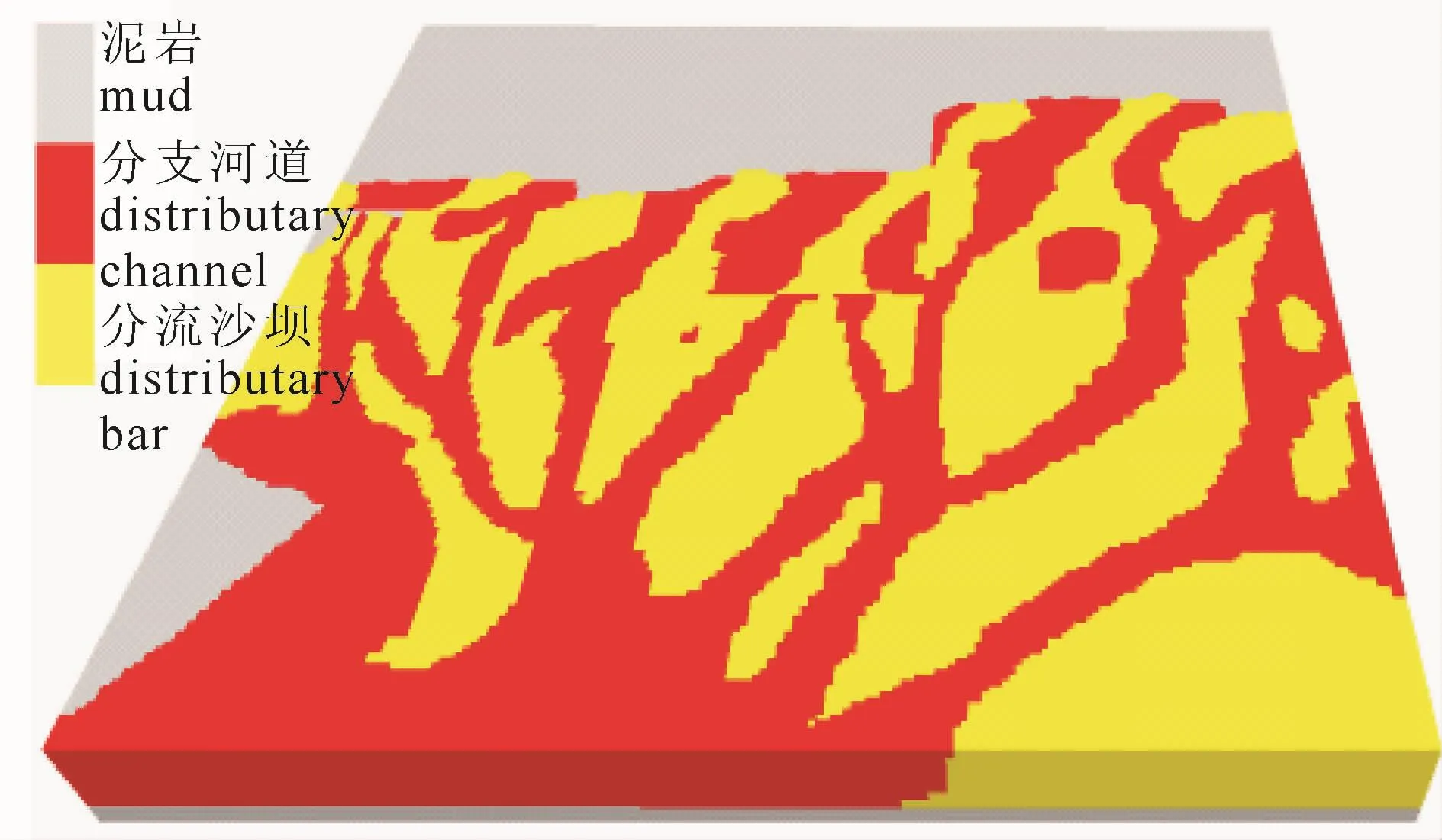
图7 新设计基于距离的方法建立的鄱阳湖储层地质模型Fig.7 the model of Poyang Lake constructed by the new designed method

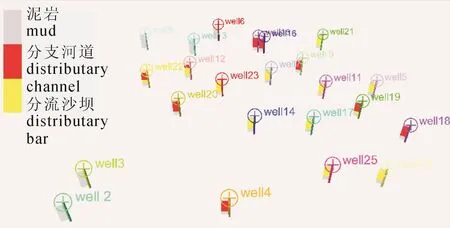
图8 合成的鄱阳湖井条件数据Fig.8 Synthesized well logs with facies of Poyang Lake

进一步的，设计了25口虚拟井，并根据其钻遇训练图像的情况给予了其相应的沉积相数据（图8），作为条件数据检验新设计方法在有井约束条件下再现沉积储层的能力。图9是新方法建立的地质模型。从建立的储层模型看，新方法建立的模型仍然反映了分流砂坝型三角洲的沉积特点和模式。由此表明新设计方法可以推广到实际地下三角洲储层建模中。

4 结论

（1）设计了一种的新的基于沉积模式的多点地质统计学方法。通过引入距离函数，建立沉积储层模式与位置关联性，再现具有空间变化性的非平稳性沉积储层空间分布，解决了传统基于平稳统计的储层建模方法难以预测非平稳储层特征的问题。

（2）基于现代鄱阳湖沉积所建立的合成非平稳性三角洲前缘沉积储层建模表明，新设计的方法较传统的建模更好地反映了三角洲相沉积储层非平稳沉积模式。新设计的方法有更好的地质适用性。