弹性液舱液体晃荡数值模拟

周上然，朱仁庆

(江苏科技大学船舶与海洋工程学院，江苏 镇江 212003)

弹性液舱液体晃荡数值模拟

周上然，朱仁庆

(江苏科技大学船舶与海洋工程学院，江苏 镇江 212003)

以流体的连续方程、N-S方程与结构动力学方程为控制方程，利用动力学软件ANSYS14.0，模拟二维矩形液舱与三维棱形液舱液体晃荡现象，用VC++语言编写矩形舱壁变形运动的响应程序，分析二维矩形液舱舱壁变形对晃荡压强的影响；利用System Coupling 模块实现三维棱形弹性液舱晃荡的双向耦合；通过提取监测点处压强，对比压强的时间历程，分析了不同板厚、不同材质对晃荡载荷的影响及不同监测点处压强变化特点。

液体晃荡；双向耦合；晃荡载荷

大型载液船舶在航行时容易引起液舱晃荡。液舱晃荡引起的晃荡载荷、结构响应以及两者之间的耦合效应，一直是大家研究和关注的焦点。研究液舱晃荡耦合效应有3种途径：理论分析、数值和实验模拟。目前，数值模拟方法运用最为广泛。李青[1](2004年)基于ALE方法，对粘性流体与弹塑性薄壁结构流固耦合问题进行求解。方智勇[2]等(2006年)将Level-set方法与通度系数方法结合，模拟了二维矩形液箱受迫晃荡运动。祁江涛[3](2007年)利用VOF法描述晃荡流场的自由液面运动，设定动网格参数，对不同几何形状的液舱晃荡进行仿真计算。端木玉[4](2007年)采用改进的Youngs 法，计算了不同液舱结构形式液舱晃荡效应。沈猛[5](2008年)采用部分单元参数法对传统VOF数值方法进行改进，对棱形液舱模型在不同装载水平于不同横摇激励频率条件下进行仿真计算。侯玲[6](2009年)基于VOF模型模拟了三维液舱晃荡，用Fluent软件的自定义函数编写程序，模拟了流体与结构之间的相互作用。本文以流体的连续方程、N-S方程与结构动力学方程为控制方程，利用动力学软件ANSYS14.0，模拟二维矩形液舱与三维棱形液舱晃荡现象，用VC++语言编写舱壁变形运动的响应程序，分析二维矩形液舱舱壁变形对晃荡压强的影响；通过对比监测点压强时间历程，分析参数变化对晃荡载荷的影响及不同监测点处压强变化特点。

1 数值方程

1.1流体运动方程

若假设流体为不可压缩粘性流，则在直角坐标系下流体的连续方程和动量守恒方程分别为：

连续方程：div(v)=0

(1)

(2)

式中：v为流场中任意一点的速度矢量；ρ为流体密度；μ为流体的粘性系数；Fb为作用在单位体积流体上质量力；P为流场压强。

1.2结构运动的微分方程

(3)

1.3流体与结构交界面条件

流固耦合交界面应满足运动学连续条件、动力学连续条件、能量守恒原理。运动学条件指在流固界面上，位移与速度一致，即：

ds=dfus=uf

(4)

动力学连续条件指在流固界面上，任意一点力的平衡，即：

σs·ns=σf·nf

(5)

能量守恒指耦合作用过程中，耦合界面上流体载荷与固体力在界面位移上所做虚功相等，即：

δus·fs=δuf·ff

(6)

式(1)～式(6)中：ds、df分别为结构、流体在耦合界面上的位移；us、uf分别为结构、流体在耦合界面上的速度；σs、σf分别为结构、流体在耦合界面上的应力；ns、nf分别为结构、流体在耦合界面上外法线方向矢量；fs、ff分别为耦合界面上固体、流体表面力；δus、δuf分别为耦合界面上固体、流体的虚位移。

2 二维液舱晃荡耦合数值模拟

考虑舱壁变形对晃荡压力的影响，以二维舱室作为研究对象，为了便于对舱壁变形运动进行编程，将舱室的侧壁简化为梁结构，结构运动的微分方程(3)可以写成以下形式：

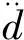
(7)

利用ANSYS14.0建立二维矩形液舱模型，模型尺寸：长度0.7 m，高度0.5 m，装载深度0.35 m，如图1。流体介质选用水。模拟高装载状态下的横荡运动，设定液舱右舱壁为柔性舱壁，可以变形，左舱壁为刚性壁；将右舱壁变形运动简化为单质点运动，运用Newmark-β法，忽略金属的阻尼，采用C语言编写质点运动的响应程序，选取适当的形函数，得出舱壁各点的运动响应，修正右舱壁网格位置，以UDF(自定义函数)为平台，结合动网格技术，采用扩散光顺方法，数值模拟液舱横荡。运动工况见表1；提取左右舱壁中间点处的压强进行对比，如图2所示。

图1 二维矩形液舱模型

表1 模型的运动工况

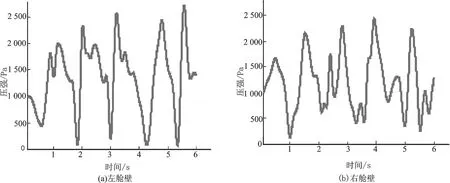
图2 左舱壁与右舱壁监测点处压强时间历程

从图2可以看出，右舱壁监测点处的压强峰值低于左舱壁监测点处，舱壁的运动变形吸收了冲击能量，降低了晃荡压强峰值；右舱壁监测点处的压强峰值之间的过渡呈现一定的“振荡”，因为作用在右舱壁上的液动压力引起了舱壁的动态响应，冲击压力的峰值衰减之后，舱壁运动产生的惯性载荷为主要作用载荷。在相同外激频率，舱壁的几何尺寸相同的情况下，刚性结构不吸收冲击能量，不发生运动变形；而弹性结构吸收了液体的部分冲击能量，会发生运动和变形，转化为结构的动能与弯曲应变能，体现了一定的动态效应。动态效应可以用动力放大系数Rd[7]来表示，计算方法如式(8)：

(8)

式中：ωn为结构的固有频率；ω为液动压力的变化频率；ξ为结构的阻尼系数，一般情况下，金属材料的取值较小，可以忽略。

ω越接近ωn，动态效应越显著。计算ωn时，要考虑附加质量的影响，通常附加质量会降低结构的固有频率。

3 三维棱形液舱晃荡耦合模拟

3.1棱形液舱模型的建立

计算模型为按照实尺度1：55进行缩比的液舱模型,如图3所示。图中,l、b、h为液舱模型长度、宽度、高度，分别为0.8、0.7、0.5 m;ru、rl为斜板上倾角与下倾角，大小取135°；hu、hl为斜顶板与斜底板的高度，大小分别为0.13、0.09 m。模型的材质选用船用钢与铝2种材质。利用ANSYS14.0 System Coupling模块实现液舱与晃荡的双向耦合。动网格光顺方法采用扩散光顺，液舱网格单元采用四边形单元，流体介质选用水。流体网格采用六面体单元。运动工况见表2。液舱模型设立5个监测点，位置见表3。

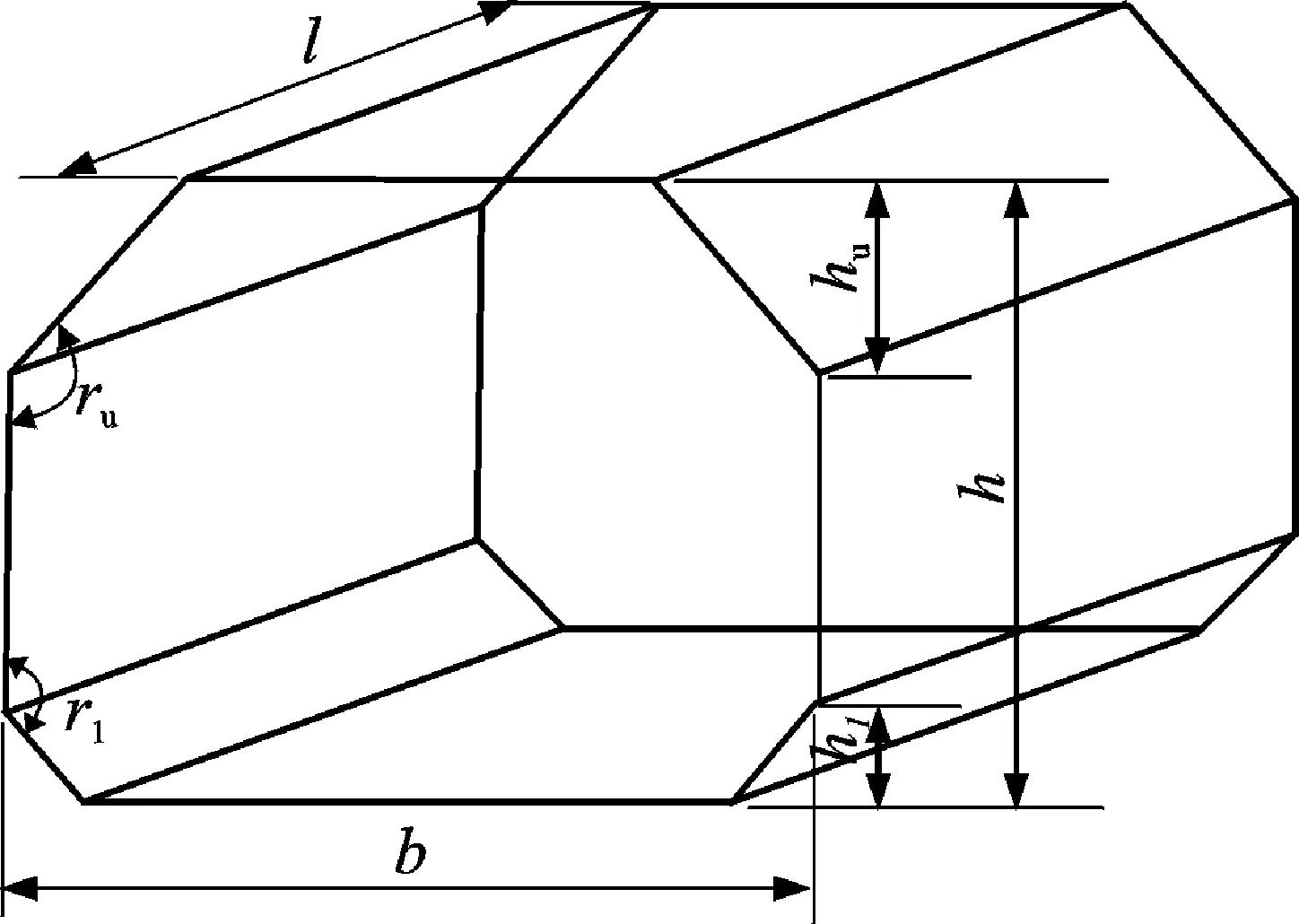
图3 液舱简化模型

3.2不同模型材质对晃荡压强的影响

取表2中工况1、工况2进行数值模拟，计算时间取5个周期：6 s。自由液面波形图见图4。分别提取钢质模型与铝质模型监测点压强时间历程，如图5与图6所示；对比监测点压强峰值，见表4。

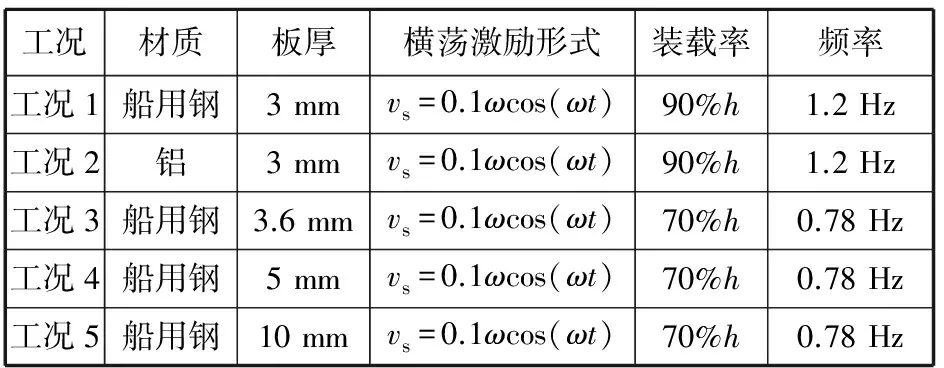
表2 模型的运动工况

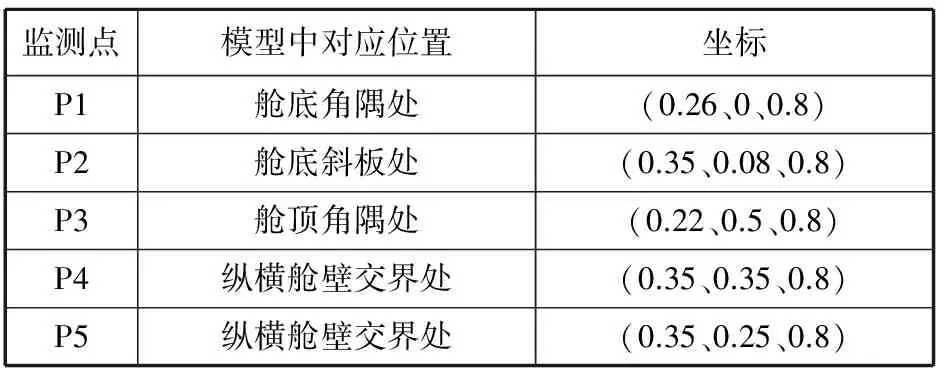
表3 监测点在模型中位置

图4 模型自由液面波形图

表4监测点P1至P4压强结果比较

材质P1点的压强幅值P2点的压强幅值P3点的压强幅值P4点的压强幅值铝5600Pa4100Pa3950Pa3150Pa船用钢6250Pa4750Pa4800Pa3900Pa

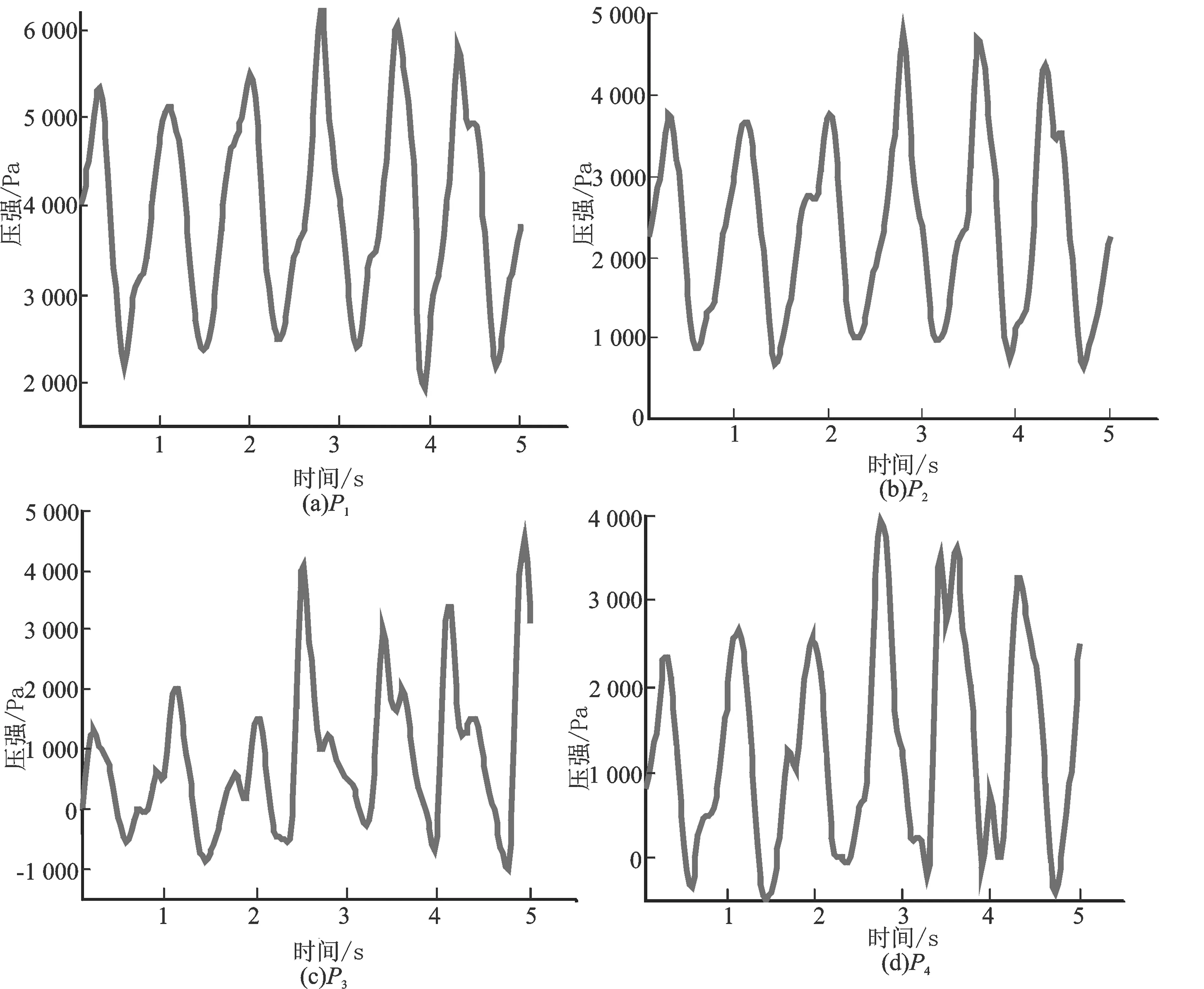
图5 钢质模型监测点(P1至P4)的压强时间历程

从图4可以看出，在高装载的液舱晃荡过程中，超过一定深度以后，在较深处的液体随着舱室一起运动；随着深度的增加，波能不断衰减。

从图5与图6可以看出，底部区域监测点的压强变化周期性特征明显，基本上与外激频率接近。自由液面附近的监测点压强变化频率较大，与舱壁的作用时间短，压强双峰特征明显，第1个峰值为液体冲击力，第2个峰值为冲击之后。因为结构的运动惯性产生的作用力，与结构的刚度、液体的冲击速度、结构的动态响应相关；压强周期性变化以振荡形式过渡；铝材质舱壁的受力明显低于钢材质舱壁，底部区域监测点的压强相差值比例低于自由液面附近的监测点的差值比例。因为随着深度的增加，舱壁对液体运动的“限制”明显增加，液体运动受限，运动没有被完全激发，所以压力以静压为主；在自由液面处，液体运动激烈，压力主要成分为冲击压强。

从表4中可以看出，2种不同的材质，相同的板厚，铝材质模型监测点的压强幅值要低于钢材质模型监测点的压强幅值。相同尺寸的相况下，2种材质的屈曲强度相差在一定的范围，弹性模量较小的材质能够体现出一定弹性效应。刚性结构的固有频率大于弹性结构的固有频率；越接近结构的固有频率，则结构的动态效应越显著，所以在同等情况下，弹性结构动态效应较大，吸收能量较多。

3.3不同板厚对舱室结构应力的影响

取表2中工况3、工况4、工况5进行模拟。计算时间取3个周期：3.6 s。自由液面波形图如图7所示。提取1.2 s时刻3种工况下模型应力云图与P5点一个周期内时间历程，如图8、图9所示。对比监测点P1、P3压强峰值与P5一个周期内的应力峰值，见表5。

表5 监测点P1、P3、P5的结果比较

图6 铝质模型监测点(P1至P4)的压强时间历程

图7 模型自由液面波形图

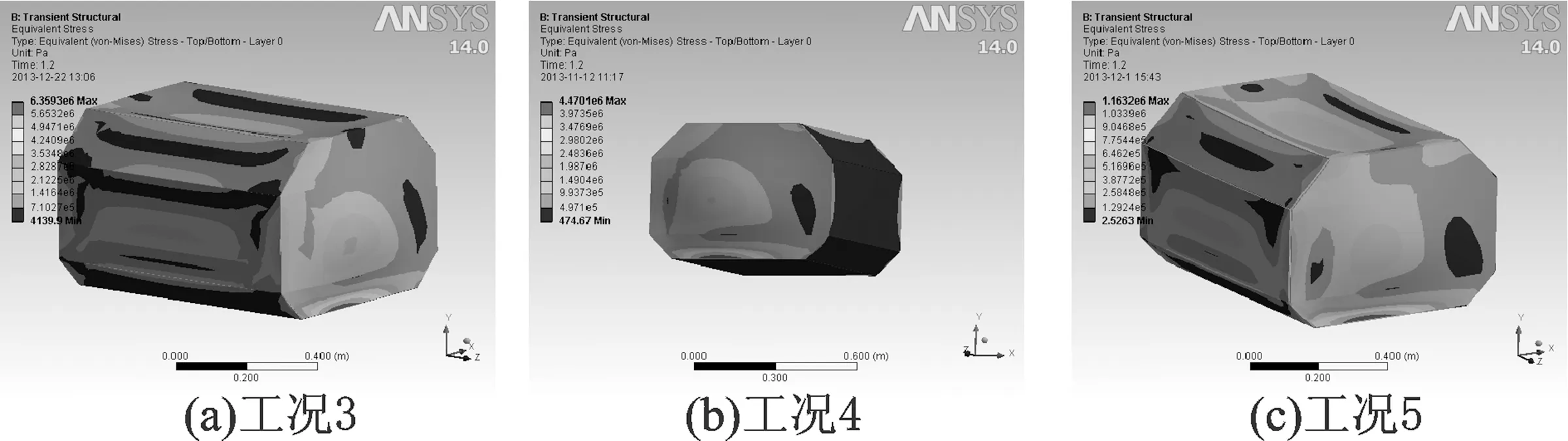
图8 1.2 s时工况3、工况4、工况5模型应力图

从图7可以看出，在高装载深度的情况下，液体晃荡极易表现出大幅驻波现象，液体冲顶现象明显。从图8可以看出，对棱型液舱来说，处于同一水平位置上的内应力越是靠近横纵舱壁交界处，其值越大。因为板交界处与角隅处受到的约束较多，所以相比模型其他部位应力较大；其次，液体晃荡冲击压力作用于舱顶，舱顶受到的冲击压力作用要显著，所以舱顶及各舱壁的交界处的应力明显大于其他部位。随着厚度的增加，模型的内应力随之降低。因此，在设计制造棱型液舱时，要对舱室的舷侧结构进行加强，重点关注角隅处及纵横舱壁交界处。矩形板条梁的内应力近似计算：

(9)

式中：Mw为矩形板内弯矩；I为截面惯性矩；Z为截面上点距中性轴的距离。

整理式(9)，得到应力近似计算公式：

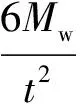
(10)

根据监测点压强图可以看出，随着板厚的增加，监测点的压强峰值略微增大。模型中舷侧板的长宽之比大于2.5，可以按照板条梁模型计算板的柔度与应力。3块板的模型的柔度均大于100，在柔性范围之内。对于矩形板，相同的外部激励，相同的长度与宽度材料属性不变，板厚超过一定的范围，板体现出刚性效应，板厚对冲击压强的影响不大，见表5。因为随着板厚的增加，板的固有频率不断增大，固有周期不断减小，动力放大系数减小；当液动压力的增长时间超过结构的固有周期时，冲击载荷对结构的作用表现为准静态加载,此时结构响应与静力分析结果相似。这种情况下，舷侧板在失稳之前，内应力σ可以按照式(10)计算，且与厚度的平方t2成反比；如果板的厚度过小，部分区域承受的内应力达到失稳应力，变成塑性板，则丧失了弹性效应。

图9 工况3、工况4、工况5模型P5点应力时间历程

4 结语

(1)在相同外激频率，舱壁的几何尺寸相同的情况下，刚性结构的固有频率大于弹性结构的固有频率；越接近结构的固有频率，则结构的动态效应越显著，所以在同样的液动压力的变化频率的情况下，弹性结构的动态效应较大，吸收了液体的部分冲击能量，会发生运动和变形，转化为结构的动能与弯曲应变能，降低了冲击作用力；冲击压力的峰值衰减之后，舱壁运动产生的惯性载荷为主要作用载荷。

(2)对比各监测点压强历程，距离自由液面较深的点压强变化相对平缓，静压起主要作用，压强增长时间较长，变化周期与液舱的运动周期接近；舱室顶点主要承受冲击压强作用，具有脉冲性特点，压强的增长时间短，能够引起结构动态响应，冲击压强的幅值具有随机性的特点；对于棱形舱室，处于同一水平位置上的晃荡压力越是靠近横纵舱壁交界处其值越大，因此要对交界处加强结构强度。高载液深度下，液体晃荡冲击压力作用于舱顶，舱顶受到的冲击压力作用要显著。

(3)对于矩形板，一定柔度范围内，相同的外部激励，相同的长度与宽度材料属性不变，板厚超过一定的范围，则板厚对冲击压强的影响不大。因为随着板厚的增加，板的固有频率不断增大，固有周期不断减小，则结构的动态效应不显著，不能吸收液体的冲击能；当晃荡载荷的作用时间超过结构固有周期，晃荡载荷对结构的作用可以等效为静载荷作用，这种情况下，舷侧板在失稳之前，内应力σ与厚度的平方t2成反比。铝材质模型监测点的压强幅值要低于钢材质模型监测点的压强幅值。相同尺寸的情况下，2种材质的屈曲强度相差在一定的范围，弹性模量较小的材质能够体现出一定的弹性效应。

[1]李青.大晃动粘性流体与储液容器的相互作用数值分析[D]. 北京：清华大学，2004.

[2]方智勇.基于Level-set法的液体晃荡与弹性结构耦合作用研究[D].镇江：江苏科技大学，2006.

[3]祁江涛,顾民. LNG船液舱晃荡的数值模拟[J].中国造船, 2007，48 (B11): 541-548.

[4]端木玉.液舱内三维液体非线性晃荡的数值模拟[D]. 镇江: 江苏科技大学, 2007.

[5]沈猛,王刚,唐文勇. 基于改进VOF法的棱形液舱液体晃荡分析[J]. 中国造船, 2009，50(1): 1-8.

[6]侯玲.液舱晃荡与弹性防晃结构的相互耦合作用的研究[D]. 镇江: 江苏科技大学, 2009.

[7]韩芳,钟冬望,蔡路军.考虑瞬态反应影响的结构动力放大系数研究[J].力学与实践,2013，35，(4):64-65.

2014-05-26

国家自然科学基金(10472032，50879030，51179077)江苏高校优势学科建设工程资助项目。

周上然(1987-)，男，硕士研究生，主要从事船舶力学研究；朱仁庆(1965-)，男，博士，教授，主要从事船舶与海洋工程载荷与响应研究。

U661.1

A