考虑几何非线性效应的大展弦比机翼气动弹性分析

杨智春，张 惠，谷迎松，宋 淼

(西北工业大学 航空学院结构动力学与控制研究所，西安 710072)

无人机机翼通常采用大展弦比构型，具有重量轻、柔性大特点；但其在气动载荷作用下会产生较大结构变形，致基于结构小变形假设的常规线性气动弹性分析方法不再适用。大展弦比机翼气动弹性分析须考虑结构大变形导致的几何非线性效应。Kim等[1]通过采用跨音速小扰动理论与大变形梁理论耦合分析大展弦比机翼几何非线性颤振特性，较好预测颤振边界。Dowell[2]对阵风响应下大展弦比机翼气动弹性特性进行理论分析与风洞实验研究，认为阵风载荷较小时几何非线性对垂向、扭转响应影响较小。Patil等[3]通过研究大展弦比机翼静/动气动弹性特性，认为大变形几何非线性对大展弦比机翼静/动气动弹性特性有重要影响。Choi等[4]采用MSC.Nastran与CFD软件耦合分析翼型(不同根梢比及后掠角)对机翼气动弹性特性影响，认为弦长不变具有锥形外截面翼型的升力系数更高、气动弹性特性更优。安效民等[5]用近似能量守恒几何大变形下壳体结构非线性动态响应算法结合求解雷诺平均N-S方程的CFD求解器发展的高效耦合格式，模拟流场非线性及结构非线性气动弹性响应。谢长川等[6]用线性化方法计算大展弦比机翼飞机在平飞设计载荷及阵风载荷作用下非线性静变形，分析结构几何非线性对大展弦比机翼固有振动特性及颤振特性影响。刘湘宁等[7]研究结构非线性对复合材料大展弦比机翼颤振特性影响结果表明，用非线性模型计算所得颤振速度小于线性模型所得颤振速度。

由以上研究知，大展弦比机翼几何非线性颤振由机翼在定常气动载荷作用下大变形所致。求解机翼非线性颤振特性前须先求解机翼在定常气动载荷作用下的静变形。为此，本文提出考虑静气动弹性效应及大变形几何非线性的大展弦比机翼气动弹性分析方法。即在给定飞行状态及机翼初始构型下求解机翼结构的定常气动载荷；采用考虑静气动弹性效应迭代方法求解大展弦比机翼结构非线性静变形，在收敛的大变形构型下获得考虑机翼结构几何非线性效应的刚度矩阵；再进行机翼的准线性模态及颤振特性分析。本文用MATALAB软件平台对MSC.Nastran软件二次开发，实现计算流程，并对大展弦比机翼模型[3]进行分析，计算该机翼非线性气动弹性特性，所得结果与文献[3]一致，验证本文所建分析方法及平台的正确性。

1 大展弦比机翼非线性气动弹性特性分析

1.1 考虑大变形几何非线性结构刚度矩阵

结构几何非线性对大展弦比机翼气动弹性特性影响主要体现于结构刚度特性随载荷工况改变及机翼非线性变形会影响机翼的气动力分布。机翼几何非线性大变形中结构应变仍为小量,因此用有限元法对大展弦比机翼结构进行几何非线性大变形分析时材料应力应变关系仍为线性，其平衡方程由变形后几何关系描述，但结构刚度特性需用切线刚度矩阵描述[8],即

K=K0+Kσ+KL

(1)

式中：K0为小位移(弹性)刚度矩阵，与单元节点位移无关；KL为大位移刚度矩阵，与单元节点位移有关；Kσ为初应力刚度矩阵。

1.2 机翼结构准线性模态分析

机翼在大变形平衡位置附近作微幅振动时可认为振动仍为线性，其振动方程为

(2)

式中：x为机翼结构偏离大变形平衡位置位移列阵；M为机翼结构质量矩阵；K为机翼结构在大变形平衡位置处切线刚度矩阵。

设机翼微振动为简谐振动：

x=Xeiωt

(3)

代入式(1)得：

KX=ω2MX

(4)

式中：ω2为特征值；X为特征向量。分别对应机翼在大变形平衡位置处的准线性模态频率及模态振型。

1.3 机翼气动载荷

对大展弦比机翼分析时可采用亚音速偶极子格网法计算其气动载荷，在各升力面网格1/4弦线处布置一马蹄涡，用加速度势偶极子模拟机翼气动力非定常项。每一气动网格单元的非定常压差为

(5)

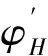
1.4 非线性静气动弹性变形分析

静气动弹性变形分析基本方程[9]为

(6)

分析单独机翼静气动弹性变形时用根部固支边界条件约束机翼结构刚体自由度。气动面定常气动力为

(7)

本文通过Matlab编程由MSC.Nastran软件的静气动弹性计算结果中提取。

进行机翼非线性静变形分析时需将空气动力通过样条插值矩阵变换为作用在结构网格节点等效力完成。样条矩阵Gkg为由结构网格点位移ug到气动力网格点位移uk的变换，可表示为

uk=Gkgug

(8)

据虚功原理，空气动力Fk及作用在结构网格节点的等效力Fg在相应虚位移上做功相等，得：

(9)

式中：δuk，δug为虚位移。

将式(8)代入式(9)得：

(10)

据虚位移任意性，得：

(11)

1.5 颤振特性分析

在机翼结构大变形平衡位置处准模态分析基础上可得机翼在模态坐标系下的颤振运动方程为

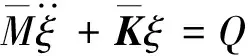
(12)

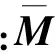
方程(12)的解可表示为

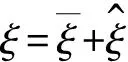
(13)

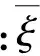
(14)

在颤振临界点，机翼小扰动振动为简谐运动,即

(15)

由式(14)可得颤振行列式为

(16)

采用p-k法求解广义特征值可得考虑机翼大变形几何非线性的颤振临界速度及颤振频率。

2 考虑结构几何非线性气动弹性特性分析

为使分析过程自动化便于工程应用，本文在Matlab软件平台上对MSC.Nastran软件进行二次开发，实现大展弦比机翼大变形几何非线性气动弹性分析方法计算流程。分析过程有三步，即考虑大变形几何非线性气动弹性静变形分析、大变形静平衡位置处准模态分析及大变形静平衡位置处颤振分析。分析流程见图1。计算过程为：① 在MSC.Patran软件中建立大展弦比机翼结构模型及气动力模型；设定机翼初始飞行状态(来流速度、飞行高度、马赫数等)，调用MSC.Nastran软件进行静气动弹性变形分析与气动载荷分析。② 用DAMP语言编程，将气动面的定常气动力转化为每个结构节点的气动载荷，将气动载荷与惯性载荷输出为各节点的外力载荷。③ 据所得节点外力载荷，用MSC.Nastran软件对结构进行大变形几何非线性分析，获得节点静变形。④ 判断变形是否收敛，若此次非线性计算所得节点静变形与前次计算结果相差达到预设精度，迭代收敛；否则，对变形机翼更新气动面计算网格，转到步骤①继续迭代。⑤ 变形收敛后提取非线性静平衡位置处切线刚度矩阵、质量矩阵，对机翼进行静平衡位置处准模态分析。⑥据图1颤振分析模块计算获得考虑大变形几何非线性的机翼颤振速度。若颤振速度与静气动弹性计算时来流速度不匹配，则更新静气动弹性分析中速度进行迭代计算，颤振速度与静气动弹性变形计算时速度一致时，该速度即为给定初速度攻角的匹配颤振速度。

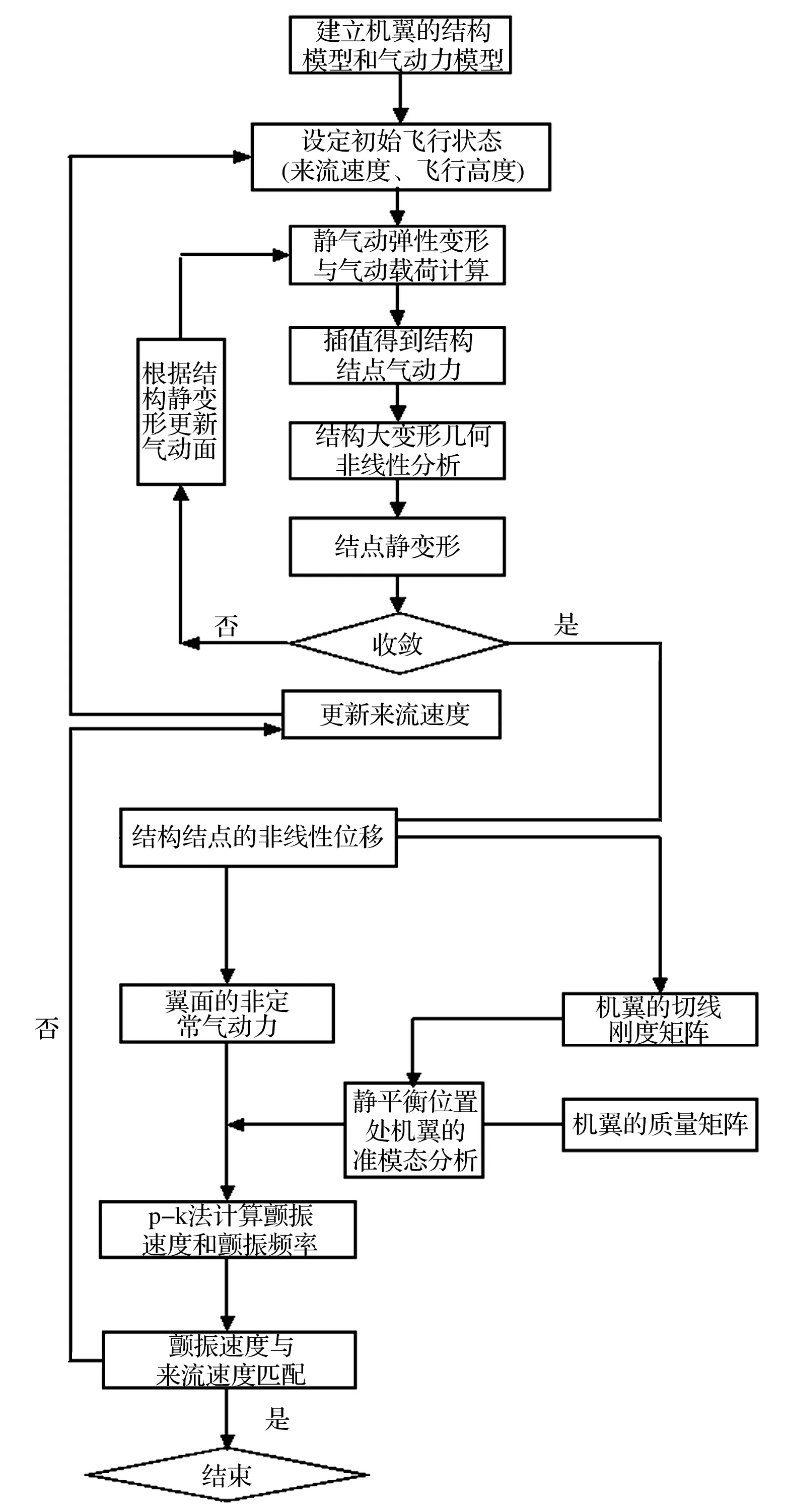
图1 考虑几何非线性效应的机翼气动弹性特性分析流程

3 考虑结构几何非线性的气动弹性特性分析算例

3.1 机翼的线性颤振分析

为对比说明大变形几何非线性对大展弦比机翼临界颤振特性影响、验证气动网格的准确性，对大展弦比机翼模型[3]的线性模态特性及颤振特性进行研究。模型数据见表1。机翼有限元模型用20个梁单元，机翼质量用分布质量。不考虑机翼大变形几何非线性因素，直接用线性振动分析所得机翼振动频率与文献[3]结果比较见表2，两者吻合较好。

表1 机翼模型数据[3]

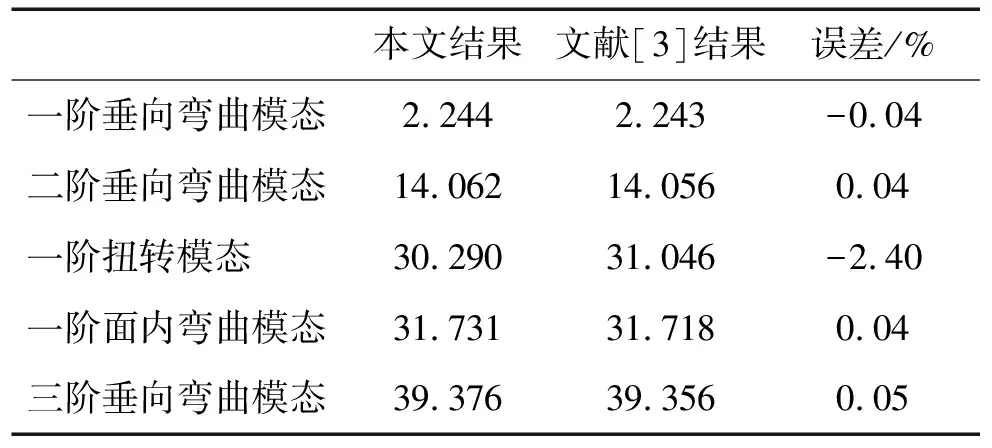
表2 线性振动分析模态频率(rad/s)

机翼线性颤振特性见表3，与文献[3]结果比较看出，颤振频率基本相同，颤振速度相对误差5.7%。分析认为该误差由本文计算非定常气动力时用亚音速偶极子网格法而文献[3]用简化片条气动力理论所致。

表3 线性颤振特性比较

3.2 机翼气动弹性特性分析

利用文献[3]算例模型,考虑大变形几何非线性因素,采用本文方法进行分析。机翼颤振速度、颤振频率随攻角变化曲线见图2(a)、(b)。文献[3]认为根部攻角在0.61°附近时颤振速度有一个跳跃，跳跃点后机翼颤振速度随攻角变大而平稳降低。本文所得翼梢变形随攻角变化规律见图2(c)。分析结果与文献[3]变化趋势一致。数值上所存差异原因同前分析。

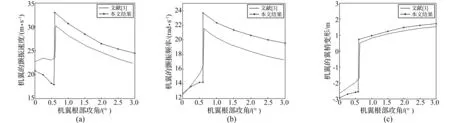
图2 机翼根部攻角对非线性气动弹性特性影响

由算例结果表明，采用本文的基于MSC.Nastran软件平台、考虑结构大变形几何非线性效应大展弦比机翼气动弹性特性分析方法求解大展弦比柔性机翼的几何非线性颤振可行，亦为工程提供简便有效手段。

4 结 论

本文通过建立考虑大变形几何非线性效应的大展弦比机翼气动弹性特性分析方法，研究大变形几何非线性效应对机翼颤振特性影响，结论如下：

(1) 颤振特性随根部攻角稳定变化后，大展弦比柔性机翼大变形所致几何非线性效应会使机翼颤振临界速度显著降低；

(2) 翼梢变形随攻角增大而增大，机翼扭转频率随翼梢变形增大而降低，机翼几何非线性颤振临界速度随攻角增大而降低。

[1] Kim K S, Lee I, Lee H K. Efficient numerical aeroelastic analysis of a high-aspect-ratio wing considering geometric nonlinearity[J]. Journal of Aircraft, 2010, 47(1):338-342.

[2] Dowell E H. Gust response for flexibly suspended high-aspect ratio wings [J]. AIAA, 2010, 48(10):2430-2444.

[3] Patil M J, Hodges D H. Nonlinear aeroelasticity and flight dynamics of high-altitude long-endurance aircraft [J]. Journal of Aircraft, 2001,38(1):88-94.

[4] Choi S, Park K,Kim J,et al. Aeroelastic characteristics of high-aspect-ratio wing according to wing shape[J]. AIAA, 2013,143:1-8.

[5] 安效民,徐敏. 一种几何大变形下的非线性气动弹性求解方法[J].力学学报,2011,43(1):98-104.

AN Xiao-min, XU Min. An improved geometrical nonlinear algorithm and its application for nonlinear aeroelasticity [J].Chinese Journal of Theoretical and Applied Mechanics, 2011,43(1):98-104.

[6] 谢长川,杨超. 大展弦比飞机几何非线性气动弹性稳定性的线性化方法[J]. 中国科学:技术科学,2011,41(3):385-393.

XIE Chang-chuan, YANG Chao. A linearization method to analyze geometrical nonlinear aeroelastic stability of the high-aspect-ratio aircraft[J]. Science China,2011,41(3):385-393.

[7] 刘湘宁, 向锦武.大展弦比复合材料机翼的非线性颤振分析[J]. 航空学报, 2006, 27(2):214-218.

LIU Xiang-ning, XIANG Jin-wu. Study of nonlinear flutter of the high-aspect-ratio composite wing[J].Chinese Journal of Aeronautics, 2006, 27(2):214-218.

[8] 吕和祥,蒋和洋. 非线性有限元[M]. 大连：化学工业出版社, 1991.

[9] Rodden W P, Johnson E H. MSC/NASTRAN version 68 aeroelastic analysis users guide[M]. New York: The MacNeal-Schwendler Corporation, 1994.

[10] Dowell E H,Traybar J,Hodges D H. An experimental-theoretical correlation study of non-linear bending and torsion deformations of a cantilever beam[J].Journal of Sound and Vibration, 1977, 50(4):533-544.