网络化控制系统鲁棒H∞保性能控制研究

刘 于 之, 李 木 国, 杜 海

( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024；2.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )



网络化控制系统鲁棒H∞保性能控制研究

刘 于 之1,2, 李 木 国*2, 杜 海2

( 1.大连理工大学 电子信息与电气工程学部, 辽宁 大连 116024；2.大连理工大学 海岸和近海工程国家重点实验室, 辽宁 大连 116024 )

针对一类含有不确定参数被控对象的网络化控制系统(NCS),研究了网络中存在时延与丢包情况下的鲁棒H∞保性能控制问题．通过Lyapunov-Krasovskii泛函和Jensen不等式,推导出闭环NCS鲁棒渐近稳定的充分条件．与已有文献相比,该充分条件可以转换为具有较少决策变量的LMI形式．给出了NCS鲁棒H∞保性能控制律的优化设计算法．最后通过数值实例验证了算法的有效性．

网络化控制系统；H∞保性能控制；线性矩阵不等式；时延；数据包丢失

0 引 言

网络化控制系统(NCS)中,不同组件之间通过共享通信介质进行信息交换,因而使系统具有布线简单、结构灵活、易于维护等众多优点,但网络的引入同时也带来诸如网络诱导延时、数据丢包、抖动以及多包传输等问题,导致控制系统的性能下降甚至不稳定,给网络控制系统的分析与设计带来了严重的困难和挑战[1]．

网络化控制系统的研究近十几年来已经得到众多国内外学者的关注．文献[2-5]中分析了 NCS的稳定性；文献[6-9]考虑了外部干扰情况下,如何设计H∞控制器的问题；文献[10-12]给出了NCS保性能控制器实现的充分条件．注意到以上文献中,NCS均被建模成具有时变时滞的连续时间系统,通过时滞系统相关理论得到系统稳定的充分条件,这些充分条件通常可转换为线性矩阵不等式(LMI)的形式．此类方法的研究重点在于如何选取合适的Lyapunov-Krasovskii泛函,以及怎样处理泛函求导过程中出现的交叉项,从而得到保守性更小的充分条件．文献[2]首先利用该方法对NCS建模,将网络诱导时延和数据丢包的影响统一建模成有界分段连续的时变输入时滞,并得到了NCS的最大允许传输延迟(MADB)．文献[9]采用与文献[2]中相同的Lyapunov-Krasovskii泛函,在求导过程中对交叉项作了更紧的界定,并利用自由权矩阵方法得到保守性更小的结果．然而以上文献均未考虑时变时滞下限的影响．文献[7]中构造了新的Lyapunov-Krasovskii泛函,由于构造的泛函中利用时滞下限的信息,降低了保守性．文献[3,6,8,12]通过构造不同Lyapunov-Krasovskii泛函,在不同程度上获得了比文献[7]保守性更小的结果．注意到以上文献中,为减小保守性,需要构造更为复杂的Lyapunov-Krasovskii泛函,或是引入额外的矩阵变量(自由权矩阵),因此导致了所得LMI决策变量的增加．本文在文献[3,6,8,12]的基础上,构造一个形式更为简洁的Lyapunov- Krasovskii泛函,通过Jensen不等式获得具有较少决策变量的LMI,进一步给出NCS的H∞保性能控制器存在的充分条件,并利用线性锥补算法实现控制器的优化求解．最后通过数值算例仿真验证该方法的有效性．

1 问题描述

考虑以下线性不确定系统:

x(t0)=x0；

z(t)=Cx(t)+Du(t)

(1)

式中:x(t)∈Rn,是系统的状态向量；u(t)∈Rm,是控制输入；w(t)∈L2[0,+∞),是外部扰动输入；z(t)∈Rq,是控制输出；x(t0)∈Rn,为系统初始状态；A、B、C、D为适维常数矩阵；ΔA(t)和ΔB(t)是反映系统模型中参数不确定性的未知矩阵,且具有以下形式:

(ΔA(t) ΔB(t))=MF(t)(EaEb)

(2)

其中F(t)是一个满足

FT(t)F(t)≤I

(3)

的不确定矩阵；M、Ea和Eb是已知的常数矩阵,它们反映了不确定参数的结构信息．

给定对称正定矩阵Q和R,定义性能函数

(4)

定义1对于不确定系统(1),若存在控制律u*(t),标量γ>0,J*>0,使得对所有允许的参数不确定性,闭环系统(1)满足如下设计指标:

(1)当w(t)≡0时,系统渐近稳定；

(2)当w(t)≡0时,系统对应的性能指标(4)具有上界J*,满足J≤J*；

(3)在零初始条件下(x(t0)=0),干扰输入w(t)和控制输出z(t)满足H∞范数约束条件:

则称u*(t)为系统(1)的一个H∞保性能控制律．

2 网络化控制系统建模

建立被控对象由式(1)描述的NCS模型,首先可做如下合理假设:

(1)网络数据传输采用单包传送,存在有界时延与数据丢包,控制器采用线性状态反馈控制律；

(2)传感器节点为时间驱动,采样周期为h；

(3)控制器节点和执行器节点采用事件驱动,当没有新数据到来时输出维持不变；

(4)系统完全可控,且所有状态可测．

注1假设(3)中包含了控制器与执行器均采用零阶保持器这一条件．

由以上假设,当考虑网络延时与丢包时,可建立如下控制系统模型[10]:

z(t)=Cx(t)+Du(t);t∈[ikh+τik,ik+1h+τik+1)

u(t+)=Kx(t-τik);t∈{ikh+τik,k=1,2,3,…}

(5)

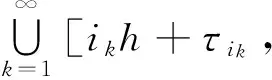
定义τ(t)=t-ikh,t∈[ikh+τik,ik+1h+τik+1),k=1,2,3,…．则系统(5)可描述为

(6)

注2在式(5)中,{i1,i2,i3,…}为{1,2,3,…}的一个子集．若ik+1=ik,说明网络传输过程中没有丢包；若ik+1>ik,说明网络传输过程中出现数据包丢失现象,且连续丢包个数为ik+1-ik-1；若ik+1ik．

为定理证明需要,给出如下引理:

引理1(Jensen不等式) 设向量函数x(t)在[a,b]上具有连续一阶导数,则对于任意给定正定对称矩阵W,有以下不等式成立:

引理2设Y、M、F、E为适当维数的实矩阵,其中F(t)满足FT(t)F(t)≤I,Y为对称矩阵,则

Y+MF(t)E+ETFT(t)MT<0

当且仅当存在一个标量ε>0,使得

Y+ε-1ETE+εMMT<0

3 主要结果

(7)

其中

Σ1=diag{-Q-1,-R-1},

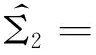
Σ3=diag{ -ε1I,-ε2I,-ε3I},

(8)

证明构造Lyapunov-Krasovskii泛函如下:

V(t)=V0(t)+V1(t)+V2(t)+V3(t)

(9)

其中

注意到τm≤τ(t)≤τM,因此由引理1可得以下不等式成立:

(10)

(11)

(12)

其中

ξ1(t)=(xT(t-τ(t)) xT(t-τM))T

ξ2(t)=(xT(t) xT(t-τ(t)))T

ξ3(t)=(xT(t-τm) xT(t-τ(t)))T

在t∈[ikh+τik,ik+1h+τik+1)上,对V(t)沿系统(6)的轨线求导并结合式(10)～(12),得

(13)

其中

ξ(t)=(xT(t) xT(t-τm) xT(t-τ(t)) xT(t-τM))T

Π22=-W2/δ, Π23=W2/δ,

Π34=W1/δ+W2/δ,

Π44=-Z-W1/δ-W2/δ,

Θ=τMW1+δW2,δ=τM-τm

若Ψ<0,则

(14)

利用Schur补定理和引理2可以得到,Ψ<0等价于

(15)

其中

Σ3=diag{-ε1I, -ε2I, -ε3I},

Γ11=(I000), Γ12=(00K0),

Γ2=(A0BK0), Γ3=(Ea0EbK0)

推论1对于系统(6),给定矩阵K,标量τm、τM满足0≤τm<τM,若存在对称正定矩阵P、Z、W1、W2,使得矩阵不等式

(16)

成立,则系统(6)鲁棒渐近稳定．

(17)

成立,其中

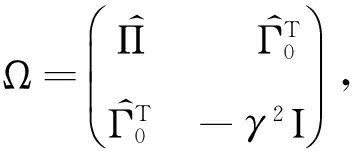
证明构造Lyapunov-Krasovskii泛函(8),由定理1的证明过程可知

(18)

其中

利用与定理1中证明类似的方法,可以证明若式(17)成立,则Λ<0成立．由此可得

(19)

(20)

推论2对于系统(6),给定矩阵K,标量γ>0,τm、τM满足0≤τm<τM,若存在对称正定矩阵P、Z、W1、W2,使得Λ<0成立,则系统是鲁棒渐近稳定的,且满足H∞扰动衰减指标γ．

(21)

成立,其中

证明略．

；i=1,2

(22)

根据Schur补定理,式(22)等价于

；i=1,2

(23)

(24)

引入新的变量Pn、W1n、W2n、L1n、L2n,式(24)可改写为

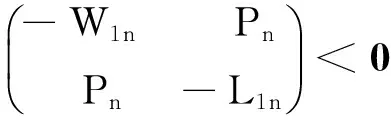
(25)

(26)

为进一步获取满足最小保性能值的控制器增益,可考虑构造以下优化问题:

minJ*

(27)

其中J*定义于式(8)．根据矩阵迹的性质,可以得到

(28)

其中

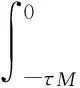
假设存在对称矩阵T、X1、X2、F满足

(29)

引入新的变量Zn使得

(30)

则根据Schur补定理,式(29)等价于

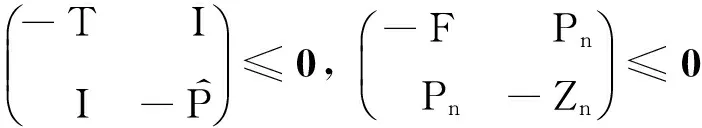
(31)

由式(28)、(29)可知,存在常数J0使得

J*≤tr(Φ0T)+tr(Φ1F)+ tr(Φ2X1)+tr(Φ3X2)≤J0

(32)

由此可以将定理3中的条件转换成如下非线性优化问题的求解:

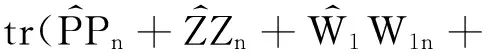
(33)

其中

若上述优化问题的解为6n,即

则式(33)中的条件有解．根据线性锥补原理(CCL),可以得到次优鲁棒H∞保性能控制器求解算法如下:

算法1

步骤1设k=0, 选择一个充分大的初始值J0>0,使得式(33)中的LMIs有可行解．

步骤2设k=1,寻找满足式(33)中LMIs的可行解:

步骤3求解下面的优化问题

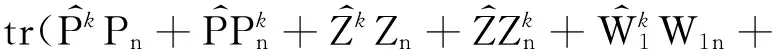
设

步骤4若步骤3中所求解满足式(22)、(29), 则减小J0然后返回步骤2； 若所求解不满足式(22)、(29)且k

注4在数值上获取式(33)的最小解6n非常困难, 因此选择式(22)、(29)作为算法终止条件．

注5算法1可以求出给定H∞干扰抑制水平γ条件下,系统的优化保性能指标J0．通过求解优化问题(33),还可以得到在给定条件下系统对外界干扰的最小抑制能力γmin．然而由于CCL算法不能保证总是找到全局最优解,通过算法1只能获得次优解．

注6定理1和定理2中控制器的求解均可采用类似算法1的步骤实现．

4 算 例

例1考虑NCS中如下被控对象:

(34)

控制器增益K=(-3.75 -11.5). 设η=0, 通过求解推论1中的矩阵不等式, 可得τm=0时,最大允许传输延迟τM=1.008 1,所得结果与文献[3,6,8]中相同,但是推论1中LMI所用决策变量个数为2(n2+n),而文献[3,6,8]中LMI所用决策变量个数分别为2.5(n2+n)、3(n2+n)、9.5(n2+n)．进一步考虑系统中存在外部干扰的情形,式(34)可表示为

z(t)=(0 1)x(t)+0.1u(t)

(35)

设τm=0,τM=0.869 5,通过求解推论2中的矩阵不等式,可得最小H∞抑制指标γmin=1.000 5,其结果与文献[6]中相同,而略大于文献[8]中的结果γmin=1.00．

例2考虑NCS中如下被控对象:

(36)

设Q=diag{0.05,0.05},R=0.1,τm=0.1,τM=1.2,利用算法1可得次优保性能指标J0=0.157 6,对应的K=(-0.713 8 -2.972 8),而文献[12]中J0=3.527 9,K=(-0.656 8 -2.411 9)．由此可见,通过算法1能得到比文献[12]中保守性更小的结果．

例3考虑系统(35)为不确定系统的情形,其中不确定参数

系统初始状态为x1(t)=0.3et+1,x2(t)=0,t∈[-0.8,0]．设Q=diag{0.1,0.1},R=0.5,τm=0.1,τM=0.8,γ=1,根据算法1可得H∞次优保性能指标J0=1.187 1,对应的K=(-1.023 3 -6.307 7)．

5 结 语

针对一类含有不确定参数被控对象的网络控制系统(NCS),研究了网络中同时存在延时与丢包情况下的鲁棒H∞保性能控制问题．构造了一个形式更为简洁的Lyapunov-Krasovskii泛函,通过Jensen不等式得到系统鲁棒渐近稳定的充分条件．分别给出了NCS保性能控制器、H∞控制器以及H∞保性能控制器存在的充分条件,并利用线性锥补算法实现了H∞保性能控制器的求解．本文方法对于NCS稳定性分析及H∞控制问题,在不影响保守性的前提下,可以得到具有较少决策变量的LMI；对于NCS保性能控制问题,能获得比已有文献保守性更小的结果．最后通过数值算例验证了本文方法的有效性

[1]Hespanha J P, Naghshtabrizi P, XU Yong-gang. A survey of recent results in networked control systems [J]. Proceedings of the IEEE, 2007,95(1):138-162.

[2]YUE Deng, HAN Qing-long, PENG Chen. State feedback controller design of networked control systems [J]. IEEE Transactions on Circuits and Systems II-Express Briefs, 2004,51(11):640-644.

[3]LI Bing, WU Jun-feng. Stability criteria of uncertain networked control systems [C] //2012International Conference on Measurement, Information and Control. Piscataway:IEEE, 2012:769-772.

[4]SUN Jian-dong, JIANG Jing-ping. Stability of uncertain networked control systems [J]. Procedia Engineering, 2011,24:551-557.

[5]ZHU Xun-lin, YANG Guang-hong. New results on stability analysis of networked control systems [C] //2008American Control Conference. Seattle:IEEE, 2008:3792-3797.

[6]JIANG X F, HAN Q L, LIU S,etal. A newH-infinity stabilization criterion for networked control systems [J]. IEEE Transactions on Automatic Control, 2008,53(4):1025-1032.

[7]YUE Deng, HAN Qing-long, Lam J. Network-based robustH∞control of systems with uncertainty [J]. Automatica, 2005,41(6):999-1007.

[8]ZHU Xun-lin, YANG Guang-hong. Network-based robustH∞control of continuous-time systems with uncertainty [J]. Asian Journal of Control, 2009,11(1):21-30.

[9]郭亚锋,李少远. 网络控制系统的H∞状态反馈控制器设计[J]. 控制理论与应用, 2008,25(3):414-420.

GUO Ya-feng, LI Shao-yuan.H∞state-feedback controller design for networked control systems [J]. Control Theory and Application, 2008,25(3):414-420. (in Chinese)

[10]PENG Chen. Networked, guaranteed cost control for a class of industrial processes with state delay [J]. Asia-Pacific Journal of Chemical Engineering, 2007,2(6):650-658.

[11]XIE Jin-song, FAN Bing-quan, Lee Young-sam,etal. Guaranteed cost controller design of networked control systems with state delay [J]. Acta Automatica Sinica, 2007,33(2):170-174.

[12]ZHOU Gu, WANG Dao-bo, CHEN Peng,etal. Guaranteed cost control for networked control system with interval time-varying delay [C] //21st Chinese Control and Decision Conference. Guilin:IEEE, 2009:538-543.

ResearchonrobustH∞guaranteedcostcontrolfornetworkedcontrolsystems

LIU Yu-zhi1,2, LI Mu-guo*2, DU Hai2

( 1.Faculty of Electronic Information and Electrical Engineering, Dalian University of Technology, Dalian 116024, China；2.State Key Laboratory of Coastal and Offshore Engineering, Dalian University of Technology, Dalian 116024, China )

RobustH∞guaranteed cost control problem for a class of uncertain networked control systems (NCS) with network-induced delay and packet dropout is investigated. A sufficient condition for robust asymptotic stability of the closed-loop NCS is derived by using Lyapunov-Krasovskii functional and Jensen′s inequality, which can be expressed as a linear matrix inequality (LMI) with fewer decision variables than those in existing literatures．An algorithm for optimization design of the robustH∞guaranteed cost control law is also presented. Numerical examples are given finally to illustrate the effectiveness of the algorithm.

networked control systems;H∞guaranteed cost control; linear matrix inequality (LMI); time delay; data packet dropout

1000-8608(2014)01-0131-08

2013-01-12；

: 2013-11-28．

国家自然科学基金资助项目(61202253).

刘于之(1986-),男,博士生,E-mail:liuyuzhi_1@163.com；李木国*(1953-),男,教授,博士生导师,E-mail:lmguo@dlut.edu.cn.

TP273

：A

10.7511/dllgxb201401020