具非线性阻尼项和源函数项双曲方程解爆破时间的下界估计
2014-09-06孙爱慧曹春玲
孙爱慧, 曹春玲
(1.吉林师范大学 数学学院, 吉林 四平 136000; 2.吉林大学 数学学院, 长春 130012)
研究简报
具非线性阻尼项和源函数项双曲方程解爆破时间的下界估计
孙爱慧1, 曹春玲2
(1.吉林师范大学 数学学院, 吉林 四平 136000; 2.吉林大学 数学学院, 长春 130012)
考虑双曲方程初边值问题解的性质.利用能量估计方法和Sobolev嵌入不等式, 给出一个具非线性阻尼项和源函数项双曲方程解爆破时间的下界估计.
阻尼项; 非线性源; 双曲方程; 爆破时间; 下界估计
考虑如下半线性双曲方程的初边值问题:
其中:Ω⊂N(N≥3)是有界区域, 且边界∂Ω滑;p>2;m>2;g≥0.许多实际问题都可以用模型(1)刻画, 例如通过渗流介质的流体过程、与温度相关的黏弹性流问题等, 文献[1-3]给出了这类问题的研究结果.当黏弹性项g=0时, 问题(1)为具有非线性阻尼项波的方程
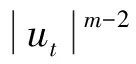
先引进如下能量泛函:
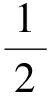
其中(g∘u)(t)=g(t-τ)‖v(t)τ.根据参考文献[10]中引理2.1, 有:
引理1如果下列条件成立, 则E′(t)≤0,t≥0且E(t)≤E1:


(H3)α=(C/k1/2)-p/(p-2),E1=(1/2-1/p)α2, 其中C为最优嵌入常数.

下面分两种情形讨论.
1) 当2 由于p>N(p-2)=μ, 应用Hölder’s不等式, 有 结合式(7),(8)有 由2(p-μ)/(Np)=2(p-Np+2N)/(Np)及不等式aαbβ≤(a+b)α+β(a>0,b>0,α>0,β>0), 有 其中:C为最优嵌入常数;q1=3-4/p>1. 2) 当2N/(N-1) 对式(10)应用不等式aαbβ≤(a+b)α+β(a>0,b>0,α>0,β>0), 有 其中:C为最优嵌入常数;q2=[2(N-2)-(N-4)p]/[2N-p(N-2)]>1. k‖‖ (13) [1]Gerbi S, Said-Houari B.Asymptotic Stability and Blow up for a Semilinear Damped Wave Equation with Dynamics Boundary Conditions [J].Nonlinear Anal, 2011, 74(18): 7137-7150. [2]LI Ke, YANG Zhijian.Exponential Attractors for the Strongly Damped Wave Equation [J].Appl Math Comput, 2013, 220: 155-165. [3]孟繁慧, 高文杰.一类具变指数源的p-Laplace方程解的爆破时间下界 [J].吉林大学学报: 理学版, 2014, 52(3): 435-438.(MENG Fanhui, GAO Wenjie.Lower Bounds for the Blow-up Time of Solutions to a Class ofp-Laplace Equation with Variable Sources [J].Journal of Jilin University: Science Edition, 2014, 52(3): 435-438.) [4]Ball J M.Remarks on Blow-up and Nonexistence Theorems for Nonlinear Evolution Equations [J].Quart J Math Oxford, 1977, 28(112): 473-486. [5]Kalantarov V K, Ladyzhenskaya O A.The Occurrence of Collapse for Quasilinear Equations of Parabolic and Hyperbolic Type [J].J Soviet Math, 1978, 10(1): 53-70. [6]Haraux A, Zuazua E.Decay Estimates for Some Semilinear Damped Hyperbolic Problems [J].Arch Ration Mech Anal, 1988, 100(2): 191-206. [8]Levine H A.Instability and Nonexistence of Global Solutions to Nonlinear Wave Equations of the FormPutt=Au+F(u) [J].Trans Amer Math Soc, 1974, 192: 1-21. [9]Levine H A.Some Additional Remarks on the Nonexistence of Global Solutions to Nonlinear Wave Equations [J].SIAM J Math Anal, 1974, 5: 138-146. [10]Messaoudi S A.Blow-up of Positive-Initial-Energy Solutions of a Nonlinear Viscoelastic Hyperbolic Equation [J].J Math Anal Appl, 2006, 320(2): 902-915. LowerBoundEstimationfortheBlow-upTimeofSolutionstoaClassofNonlinearDampedHyperbolicEquationswithSources SUN Aihui1, CAO Chunling2 The authors studied the properties of solutions for the initial boundary value problem to a hyperbolic equation and obtained a lower bound estimation of blow-up time for a class of nonlinear damped hyperbolic equations with sources by using the method of energy estimate and Sobolev embedding inequalities. damped term; nonlinear sources; hyerbolic equations; blow-up time; lower bound estimation 2014-07-14. 孙爱慧(1978—), 女, 汉族, 硕士, 讲师, 从事偏微分方程的研究, E-mail: sunaihui2002@126.com. 吉林省自然科学基金(批准号: 20115222)、吉林省科技发展计划项目(批准号: 201201082; 201201081)和吉林省教育厅“十二五”科学技术研究项目(批准号: 吉教科合字[2013]第445号). O175.8 A 1671-5489(2014)06-1227-03 10.13413/j.cnki.jdxblxb.2014.06.24 赵立芹)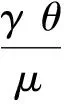
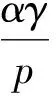

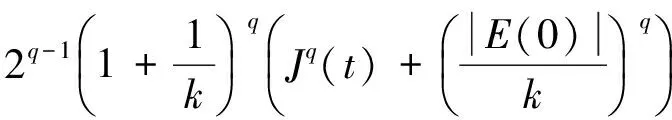
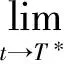
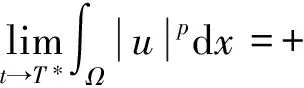
(1.CollegeofMathematics,JilinNormalUniversity,Siping136000,JilinProvince,China;
2.CollegeofMathematics,JilinUniversity,Changchun130012,China)
