一类非本原代换诱导的超空间系统

汪 威, 李 健, 朱晓刚, 廖梦兰, 李俊杰

(1.吉林农业大学 信息技术学院, 长春 130118； 2.长春工程技术学院, 长春 130117；3.吉林大学 数学研究所, 长春 130012)

研究简报

一类非本原代换诱导的超空间系统

汪 威1, 李 健1, 朱晓刚2, 廖梦兰3, 李俊杰1

(1.吉林农业大学 信息技术学院, 长春 130118； 2.长春工程技术学院, 长春 130117；
3.吉林大学 数学研究所, 长春 130012)

考虑具有两个符号等长的非本原代换诱导的超空间系统的Li-Yorke混沌性, 利用该代换系统存在Li-Yorke混沌集的条件, 进一步得出了其诱导的超空间系统存在Li-Yorke混沌集和不存在Li-Yorke混沌集的条件.

非本原代换; 超空间系统; Li-Yorke混沌

0 引 言

混沌性在农业生产中应用广泛, 如玉米产量的预测、小麦病虫害预报及灌区水资源优化等.关于代换系统的混沌性研究目前已有一些成果, 如文献[1]讨论了具有两个符号本原代换诱导的子移位的Li-Yorke混沌性态及不存在分布混沌对的性质; 文献[2]给出了一类非本原等长代换诱导的子移位的混沌性; 文献[3]探讨了非本原非等长代换的混沌性; 文献[4]给出了一类代换系统是Li-Yorke混沌的充要条件及不是分布混沌的一个充分条件.本文研究由两个符号非本原等长代换诱导的子移位的超空间系统的混沌性态.

设(X,f)为紧致系统,d是X的一个拓扑度量, 如果Y⊂X中任何不同两点x,y都满足:

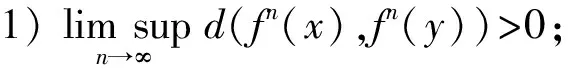
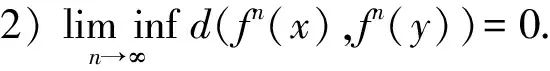
则称Y为f的Li-York混沌集.

文献[5-6]给出了一些动力性质在紧致系统及其诱导的超空间系统上的等价关系.本文涉及的有关超空间系统的定义及记号参见文献[7].

设(X,J)是一个拓扑空间,P(x)表示X的所有非空子集构成的集合,G1,G2,…,Gn是X的n个非空开集, 令

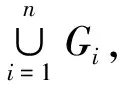
则所有形如B(G1,G2,…,Gn)的集合构成了空间P(x)某个拓扑的基, 该拓扑称为Vietoris拓扑.该拓扑空间记作(P(X),Jv), 也称为(X,J)的超空间.本文主要考察空间(X,J)的闭集类, 即K(X)={K∈P(X);K是X的非空紧子集}.

设(X,d)为紧致度量空间.对任意的A,B∈K(X), 令ρ*(A,B)=inf{ε>0:A⊂N(B,ε)}, 称为集合A,B的Hausdorff分离.其中N(B,ε)={x∈X;d(x,A)<ε}.H(A,B)=max{ρ*(A,B),ρ*(B,A)}称为K(X)上的Hausdorff度量.

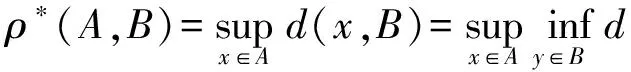
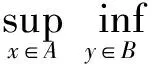
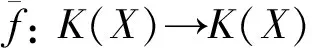
1 非本原代换

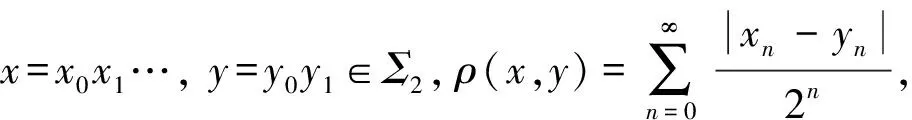
定义1设η为符号空间Σ2上的等长代换, 定义为η(0)=a=a0a1…an-1,η(1)=b=b0b1…bn-1, 且满足条件: 1)a0=0; 2) 存在i>0, 使得ai=1.则η在Σ2中有一个以0开头的不动点, 记作u.

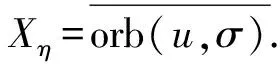
定义2如果0η(1), 即η(1)包含0, 则称η是本原的; 否则称η是非本原的.

下面假设f是由等长代换η诱导的代换子移位, 并且假设：

(H1) 存在不同的s1,s2,t∈{0,1,…,n-1}, 使得as1≠bs1,as2≠bs2, 并且at=bt.

引理1[8]设η是非本原代换, 则有如下结论:

1) 若η满足条件(H1), 则其诱导映射f有c稠密的Li-Yorke混沌集；

2) 若η不满足条件(H1), 则其诱导映射f没有Li-Yorke混沌集.

2 存在Li-Yorke混沌集的条件

证明: 由引理1中1)可知,η满足条件(H1), 则η存在Li-Yorke混沌集S⊂Xη, 使得对任意的x,y∈S, 都有

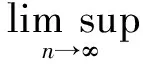
而{{x},{y}}⊂K(Xη), 则

ρ*({x},{y})=ρ(x,y),ρ*({y},{x})=ρ(y,x),

对应的Hausdorff度量为

H({x},{y})=max{ρ*({x},{y}),ρ*({y},{x})}=ρ(x,y).

于是, 对上述{x},{y}, 有

3 不存在Li-Yorke混沌集的条件

证明: 根据定义1,η满足条件a0=0.若η不满足条件(H1), 则对任意的i>0, 都有ai=1,η存在一个以0开头的不动点, 记为u=011…, 并且按照Xη的定义, 在Xη中只有两个点, 即v=111…和不动点u=011….因而, 集合K(Xη)是有限集, 即K(Xη)={{u},{v},{u,v}}.

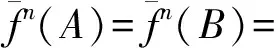
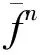
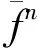
[1]廖公夫, 范钦杰, 王立冬.一类本原代换与混沌集 [J].中国科学A辑: 数学, 2008, 38(4)： 469-476.(LIAO Gongfu, FAN Qinjie, WANG Lidong.A Class of Primitive Substitutions and Chaotic Sets [J].Science China Series A: Mathematics, 2008, 38(4)： 469-476.)

[2]廖公夫, 汪威, 范钦杰.一类非本原代换与混沌 [J].数学年刊, 2009, 30A(2)： 183-188.(LIAO Gongfu, WANG Wei, FAN Qinjie.A Class of Non-primitive Substitutions and Chaos [J].Chinese Annals of Mathematics, 2009, 30A(2): 183-188.)

[3]楚振艳, 廖丽.一类非本原代换系统的拓扑熵与混沌 [J].吉林大学学报: 理学版, 2011, 49(6)： 1053-1054.(CHU Zhenyan, LIAO Li.Topological Entropy and Chaos for a Class of Non-primitive Substitution Systems [J].Journal of Jilin University: Science Edition, 2011, 49(6)： 1053-1054.)

[4]王宏仁, 廖丽, 范钦杰.一类非本原代换系统的混沌性态 [J].吉林大学学报: 理学版, 2011, 49(2): 240-242.(WANG Hongren, LIAO Li, FAN Qinjie.Chaotic Behaviors for a Class of Non-primitive Substitution Systems [J].Journal of Jilin University: Science Edition, 2011, 49(2): 240-242.)

[5]马先锋.一类超空间上的离散动力系统 [D].长春: 吉林大学, 2006.(MA Xianfeng.Discrete Dynamical Systems for Some Hyperspaces [D].Changchun: Jilin University, 2006.)

[6]MA Xianfeng, HOU Bingzhe, LIAO Gongfu.Chaos in Hyperspace System [J].Chaos Solitons Fractals, 2009, 40(2): 653-660.

[7]Klein E, Thompson A.Theory of Correspondences [M].New York: Wiley-Inter-Science, 1984.

[8]廖公夫, 王立冬, 范钦杰.映射迭代与混沌动力系统 [M].北京： 科学出版社, 2013.(LIAO Gongfu, WANG Lidong, FAN Qinjie.Mapping Iteration and Chaotic Dynamical System [M].Beijing: Science Press, 2013.)

HyperspaceSystemInducedbyaClassofNon-primitiveSubstitution

WANG Wei1, LI Jian1, ZHU Xiaogang2, LIAO Menglan3, LI Junjie1
(1.CollegeofInformationTechnology,JilinAgriculturalUniversity,Changchun130118,China;
2.InstituteofChangchunEngineeringTechnology,Changchun130117,China;
3.InstituteofMathematics,JilinUniversity,Changchun130012,China)

We discussed Li-Yorke chaotic properties for hyperspace systems induced by non-primitive substitutions on two symbols.With the help of the conditions of containing Li-Yorke chaotic sets in the substitution system, we obtained the conditions for the hyperspace systems to contain Li-Yorke chaotic sets and not to contain Li-Yorke chaotic sets.

non-primitive substitution; hyperspace system; Li-Yorke chaos

2014-07-02.

汪 威(1981—), 女, 汉族, 博士, 讲师, 从事拓扑动力系统的研究, E-mail: maggie0403@126.com.

吉林省科技发展计划项目(批准号： 20140204045NY; 20130522110JH)、吉林省教育厅“十二五”科学技术研究项目(批准号： 吉教科合字[2014]第468号)和吉林农业大学科研启动基金(批准号： 201310).

O189

A

1671-5489(2014)06-1219-03

10.13413/j.cnki.jdxblxb.2014.06.22

赵立芹)