一类反周期分数阶q-差分边值问题解的存在性
2014-09-06孙明哲侯成敏
孙明哲, 侯成敏
(延边大学 理学院数学系, 吉林 延吉 133002)
(f)(x)=(x-qt)(α-1)f(t)dqt, α>0, x∈[0,1],
研究简报
一类反周期分数阶q-差分边值问题解的存在性
孙明哲, 侯成敏
(延边大学 理学院数学系, 吉林 延吉 133002)
利用基本的不动点定理研究一类带有反周期非线性分数阶q-差分方程边值问题, 得到了边值问题解的存在与唯一的充分条件, 并通过具体方程验证了所得结论.
分数阶q-差分; 边值问题; 不动点定理
q-微积分在量子力学、核及高能物理等研究领域应用广泛.文献[1-3]给出了分数阶q-微积分的基本概念和性质; 文献[4-9]给出了分数阶q-差分边值问题的研究成果.但对于含有分数阶边值条件的边值问题目前报道很少, 本文讨论带有分数阶边值条件的q-差分边值问题:
解的存在性和唯一性, 其中: 1<α<2, 0<ν<1为常数;f(t,u(t)): [0,1]×[0,+∞)→为连续函数是Caputo分数阶q-导数.
定义1[8]分数阶q-积分定义为
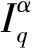
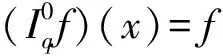

引理1[10]设X是一个Banach空间,T:X→X是一个完全连续算子, 集合V={u∈X|u=μTu, 0<μ<1}有界, 则算子T在X上有不动点.
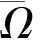
定理1设1<α<2, 0<ν<1, 则u(t)是问题(1)解的充要条件是u(t)有如下形式:
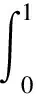
其中
证明: 假设u(t)是问题(1)的解, 则有
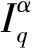
利用边值条件(2)解得
将C1,C2代入式(4)得式(3).反之, 如果u(t)满足式(3), 则易推出u(t)是问题(1)-(2)的解.证毕.
记Banach空间C=C([0,1],), 赋范数‖u‖|u(t)|.定义算子T:C→C, 且
由定理1知问题(5)有解当且仅当算子T有不动点.
定理2假设对于t∈[0,1],u∈C, 存在常数M>0, 满足|f(t,u)|≤M, 则问题(1)-(2)至少存在一个解.
证明: 首先, 考虑算子T是完全连续的.由f的连续性易知T是连续的.令Ω⊂C有界, 则由u∈Ω, |f(t,u)|≤M, 得
表明‖Tu(t)‖≤M2, 此外
因此对于t1,t2∈[0,1],t1 故T在[0,1]上是等度连续的, 由Arzela-Ascoli定理知, 算子T:C→C是完全连续的. 其次, 考虑集合V={u∈C|u=μTu, 0<μ<1}有界.若u∈V,u=μTu, 0<μ<1, 对于任意的t∈[0,1], 有|u(t)|≤μ|Tu(t)|≤|Tu(t)|≤M2, 从而对于任意的t∈[0,1], 有‖u(t)‖≤M2, 即V有界. 由引理1知,T至少有一个不动点, 即问题(1)-(2)至少存在一个解.证毕. 定义Ω={u∈C|‖u‖ 由引理2知,T至少有一个不动点, 即问题(1)-(2)至少存在一个解. 定理4假设f: [0,1]×→为连续函数, 满足|f(t,u)-f(t,v)|≤L|u-v|, ∀t∈[0,1],u,v∈且L<, 则问题(1)-(2)存在唯一解. 因此‖(Tu)(t)‖≤r. 对于u,v∈C,t∈[0,1], 有 例1考虑边值问题 易知 满足定理2的假设条件, 因此问题(6)至少有一个解. 例2考虑边值问题 例3考虑边值问题 满足定理4的假设条件, 故问题(8)有唯一解. [1]Jackson F H.q-Difference Equations [J].Amer J Math, 1910, 32(4): 305-314. [2]Al-Salam W A.Some Fractionalq-Integrals andq-Derivatives [J].Proc Edinb Math Soc, 1966/1967, 15(2): 135-140. [3]Agarwal R P.Certain Fractionalq-Integrals andq-Derivatives [J].Proc Cambridge Philos Soc, 1969, 66: 365-370. [4]YANG Wengui.Positive Solutions for Boundary Value Problems Involving Nonlinear Frationalq-Difference Equations [J].Differ Equ Appl, 2013, 5(2): 205-219. [5]ZHAO Yulin, CHEN Haibo, ZHANG Qiming.Existence and Multiplicity of Positive Solutions for Nonhomogeneous Boundary Value Problems with Fractionalq-Derivative [J].Bound Value Probl, 2013, 2013: 103. [6]ZHAO Yulin, YE Guobing, CHEN Haibo.Multiple Positive Solutions of a Singular Semipositone Integral Boundary Value Problem for Fractionalq-Derivatives Equation [J/OL].Abstr Appl Anal, 2013.http: dx.doi.org/10.1155/2013/643571. [7]Ferreira R A C.Nontrivial Solutions for Fractionalq-Difference Boundary Value Problems [J].Electron J Qual Theory Differ Equ, 2010, 70(10): 1-10. [8]Ahmad B, Nieto J J.Anti-periodic Fractional Boundary Value Problems with Nonlinear Term Depending on Low Order Derivative [J].Fractional Calculus and Applied Analysis, 2012, 15(3): 451-462. [9]WANG Fang, LIU Zhenhai.Anti-periodic Fractional Boundary Value Problems for Nonlinear Differential Equations of Fractional Order [J].Adv Differ Equ, 2012, 2012: 116. [10]Smart D R.Fixed Point Theorems [M].Cambridge: Cambridge University Press, 1980. ExistenceofSolutionsforaClassofAnti-periodicBoundaryValueProblemswithFractionalq-DifferenceEquations SUN Mingzhe, HOU Chengmin We studied a class of the fractionalq-differences boundary value problem with the fractionalq-differences boundary conditions with the aid of some standard fixed point theorems, obtaining sufficient conditions for the existence and uniqueness results of solutions.As the application, some equations were presented to illustrate the main results. fractionalq-difference; boundary value problem; fixed point theorem 2014-01-23. 孙明哲(1979—), 女, 汉族, 硕士, 讲师, 从事微分方程理论及应用的研究, E-mail: mzsun@ybu.edu.cn.通信作者: 侯成敏(1964—), 女, 汉族, 硕士, 教授, 从事微分方程理论及应用的研究, E-mail: cmhou@foxmail.com. 国家自然科学基金(批准号: 11161049)和吉林省教育厅“十二五”科学技术研究项目(批准号: 吉教科合字[2014]第20号). O175.8 A 1671-5489(2014)06-1215-04 10.13413/j.cnki.jdxblxb.2014.06.21 赵立芹)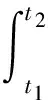
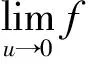
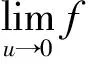
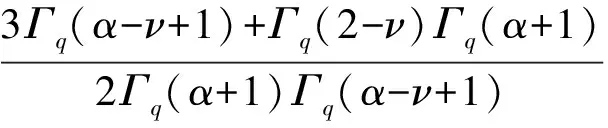

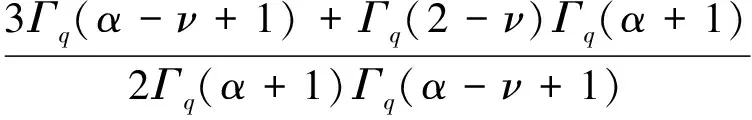
(DepartmentofMathematics,CollegeofScience,YanbianUniversity,Yanji133002,JilinProvince,China)
