KdV-Burgers方程的重正化群方法

黄开银, 田 华, 杨双羚

(1.吉林大学 数学学院, 长春 130012； 2.东北师范大学 数学与统计学院, 长春 130024)

研究快报

KdV-Burgers方程的重正化群方法

黄开银1, 田 华1, 杨双羚2

(1.吉林大学 数学学院, 长春 130012； 2.东北师范大学 数学与统计学院, 长春 130024)

利用重正化群方法研究一类KdV-Burgers方程的奇异摄动问题, 得到了该方程的一致有效渐近展开式.

重正化群方法； 奇异摄动； KdV-Burgers方程

考虑如下KdV-Burgers方程：

它是一类较普遍的具有物理特性的非线性演化方程, 应用广泛, 目前已取得了许多研究结果, 如Cavalcanti等[1]研究了带有不定阻尼项KdV-Burgers方程Cauchy问题的指数稳定性; Yang等[2]研究了耦合KdV-Burgers方程的精确解; Molabahrami等[3]求得了一类KdV-Burgers方程的数值解; Jun等[4]运用改进三角函数法求得了组合KdV-Burgers方程的显式精确解.本文主要利用重正化群方法[5-11]研究KdV-Burgers方程的奇异摄动问题.

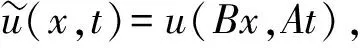
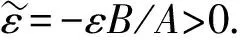
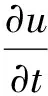
（2）

为讨论方便, 本文考虑方程(2)在2π周期边值条件下的解, 对于更一般周期条件的讨论完全一致.

令Ω=(0,2π), 并记

H(Ω)={u(x)|u(x)∈C3(),u(x+2π)=u(x),x∈},

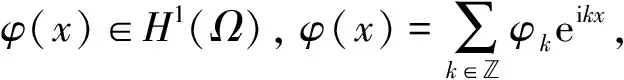
是方程(2)满足初边值条件

证明: 为方便, 记算子L=-∂xx+∂xxx,F(u)=uux, 则初边值问题(2)-(4)可改写为

假设初边值问题(5)的解u(x,t)有如下渐近展开式:

将式(6)代入式(5), 并对比等式两端ε的同次幂系数得

将式(9)代入式(8)得

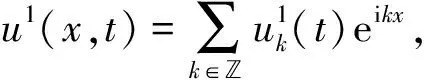
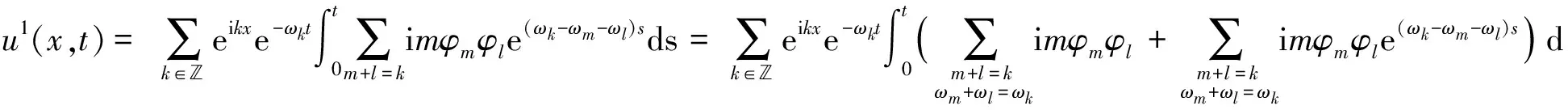
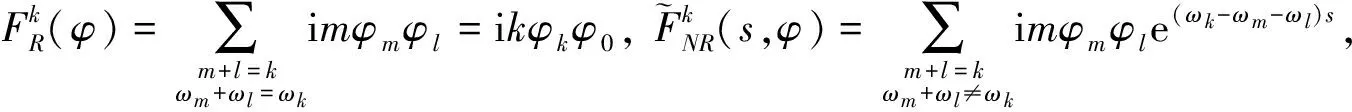
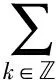
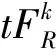
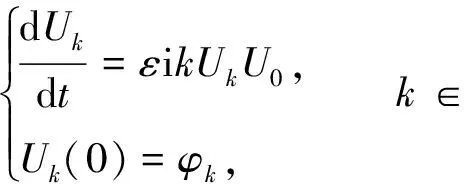
（12）

式(12)称为重正化群方程, 解得

Uk(t)=φkeiεkφ0t.

（13）

因此, 问题(2)-(4)的一致有效渐近展开式为

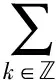
其中Uk(t)由式(13)给出.证毕.

[1]Cavalcanti M M, Domingos Cavalcanti V N, Komornik V, et al.Global Well-Posedness and Exponential Decay Rates for a KdV-Burgers Equation with Indefinite Damping [J].Ann Inst H Poincaré Anal Non Linéaire, 2014, 31(5): 1079-1100.

[2]YANG Shaojie, HUA Cuncai.Lie Symmetry Reductions and Exact Solutions of a Coupled KdV-Burgers Equation [J].Appl Math Comput, 2014, 234: 579-583.

[3]Molabahrami A, Khani F, Hamedi-Nezhad S.Soliton Solutions of the Two-Dimensional KdV-Burgers Equation by Homotopy Perturbation Method [J].Physics Letters A, 2007, 370(5/6): 433-436.

[4]JUN Yu, KE Yunquan, ZHANG Weijun.New Traveling Wave Solutions to Compound KdV-Burgers Equation [J].Communi Theor Phys, 2004, 41(4): 493-496.

[5]Kunihiro T.The Renormalization-Group Method Applied to Asymptotic Analysis of Vertor Fields [J].Progr Theor Phys, 1997, 97(2): 179-200.

[6]Chiba H.Simplified Renormalization Group Method for Ordinary Differential Equations [J].J Differ Equ, 2009, 246(5): 1991-2019.

[7]Ziane M.On a Certain Renormalization Group Method [J].J Math Phys, 2000, 41(5): 3290-3299.

[8]吴克义, 付苗苗, 吕显瑞.重正化群方法在一类奇异摄动边值问题中的应用 [J].吉林大学学报： 理学版, 2005, 43(5): 599-602.(WU Keyi, FU Miaomiao, LÜ Xianrui.Renormalization Group Method Applied in a Class of Singular Perturbation Boundary Value Problems [J].Journal of Jilin University: Science Edition, 2005, 43(5): 599-602.)

[9]Moise I, Ziane M.Renormalization Group Method.Application to Partial Differential Equations [J].J Dynam Differ Equ, 2001, 13(2): 275-321.

[10]CHEN Linyuan, Goldenfeld N, Oono Y.Renormalization Group and Singular Perturbations: Multiple Scales, Boundary Layers, and Reductive Perturbation Theory [J].Phys Rev E, 1996, 54(1): 376-394.

[11]Kunihiro T.A Geometrical Formulation of the Renormalization Group Method for Global Analysis [J].Progr Theor Phys, 1995, 94(4): 503-514.

RenormalizationGroupMethodfortheKdV-BurgersEquation

HUANG Kaiyin1, TIAN Hua1, YANG Shuangling2
(1.CollegeofMathematics,JilinUniversity,Changchun130012,China;
2.SchoolofMathematicsandStatistics,NortheastNormalUniversity,Changchun130024,China)

The singular perturbation initial-boundary value problem of the KdV-Burgers equation was discussed.Using the renormalization group (RG) method, we gave the uniformly valid asymptotic expansion for the problem.

renormalization group method; singular perturbation; KdV-Burgers equation

2014-09-22.

黄开银(1990—), 男, 汉族, 硕士研究生, 从事常微分方程理论及应用的研究, E-mail: huangky1010@163.com.通信作者： 田 华(1968—), 女, 汉族, 高级工程师, 从事常微分方程理论及应用的研究, E-mail: thua@jlu.edu.cn.

国家自然科学基金青年基金(批准号： 11301210).

O175.12

A

1671-5489(2014)06-1207-03

10.13413/j.cnki.jdxblxb.2014.06.19

赵立芹)