长程相依过程精确渐近性的一般结果
2014-09-06关丽红赵亚男
关丽红, 赵亚男
(长春大学 理学院, 长春 130022)
长程相依过程精确渐近性的一般结果
关丽红, 赵亚男
(长春大学 理学院, 长春 130022)
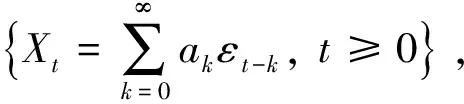
长程相依过程; 矩完全收敛性; 精确渐近性; 一般结果; 分数积分过程
0 引言及主要结果
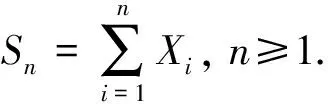
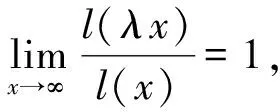
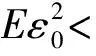
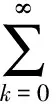
(H1) {ak,k≥0}为满足条件ak~k-αl(k)的实数序列, 1/2<α<1;
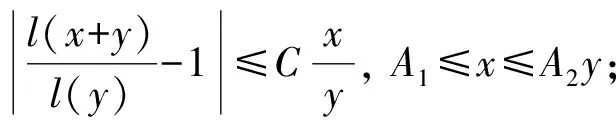
(H3)g(x)为[n0,∞)上具有非负导数g′(x)的正值可导函数, 且g(x)↑∞,x→∞;
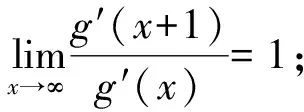
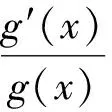
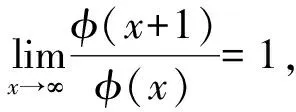
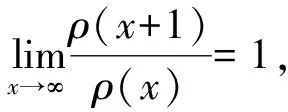
本文的主要结果如下.
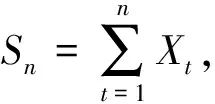
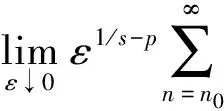
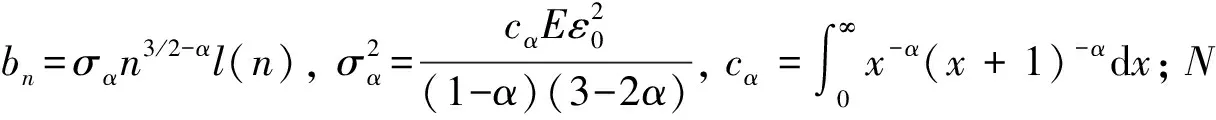
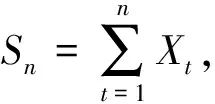
其中bn,N定义如定理1.
注1满足假设条件(H2)的缓变函数有很多[16], 如l(x)=(logx)β, (loglogx)γ, elogδx, 其中:β,γ为实数; 0<δ<1.
注2满足假设条件(H3)~(H7)的g(x)有很多, 如g(x)=xα, (logx)β, (loglogx)γ, 其中α>0,β>0,γ>0为某些适当的参数.
注3在定理1中, 令s=1/2, 0≤p<2,g(x)=x, 则可得文献[13]中的定理1.2; 令1/s=β(δ+1),p=2,g(x)=(logx)δ+1, 其中β≥2,δ>2/β-1, 则可得文献[13]中的定理1.3.在定理2中,令p=2,s=1/2,g(x)=x, 则可得文献[13]中的定理1.1, 因此本文推广了长程相依过程的已有结果.
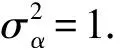
1 定理的证明
引理1[15]假设{Xt}为式(1)定义的满足条件(H1)和(H2)的长程相依过程, 则
其中:bn如定理1所定义;W(s)为分数布朗运动.
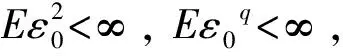
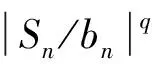
其中bn如定理1所定义.
令A(ε)=[g-1(Mε-1/s)], 其中:g-1(x)为g(x)的反函数;M≥1.
命题1在定理1的假设条件下, 有
证明: 利用引理1和引理2, 类似文献[12]中命题1的证明可得.
命题2在定理1的假设条件下, 对于p>0, 有
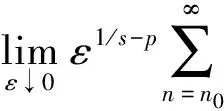
证明: 类似文献[8]中命题5.1的证明可得.
命题3在定理1的假设条件下, 对于p>0, 有
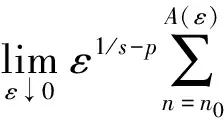
证明: 显然
其中:
先估计Δn1.注意到n≤A(ε)即εgs(n)≤Ms, 则有
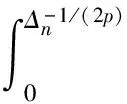
其次估计Δn3.注意到正态分布的任意阶矩都存在, 则由Markov不等式, 有
最后估计Δn2.由Markov不等式和引理2, 并注意到q>1/s>p>0, 有
根据引理1, 当n→∞时,Δn→0, 因此由式(6)~(9), 可得
Δn1+Δn2+Δn3→0,n→∞.(10)
再由式(10)、φ(x)的单调性以及Toeplitz引理[24], 可知式(5)成立.证毕.
命题4在定理1的条件下, 对于p>0, 有
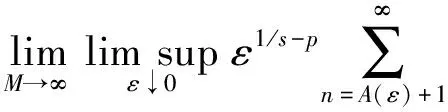
证明: 类似文献[8]中命题5.3的证明可得.
命题5在定理1的条件下, 对于p>0, 有
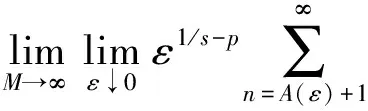
证明: 注意到q>1/s>p>0, 由Markov不等式及引理2, 有
下面证明定理1.当p=0时, 由于
则由命题1可知定理1成立.当1/s>p>0, 注意到
故要证明式(2), 只需证明下列两式成立即可:
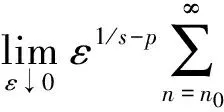
由命题1可知式(13)成立, 由命题2~命题5以及三角不等式可知式(14)成立, 从而式(2)成立.
定理2的证明与定理1的证明类似.
[1]Hsu P L, Robbins H.Complete Convergence and the Strong Law of Large Numbers [J].Proc Nat Acad Sci USA, 1947, 33(2): 25-31.
[2]Heyde C C.A Supplement to the Strong Law of Large Numbers [J].J Appl Probab, 1975, 12: 173-175.
[3]Gut A, Spătaru A.Precise Asymptotics in the Baum-Katz and Davis Laws of Large Numbers [J].J Math Anal Appl, 2000, 248(1): 233-246.
[4]WANG Yuebao, YANG Yang.A General Law of Precise Asymptotics for the Counting Process of Record Times [J].J Math Anal Appl, 2003, 286(2): 753-764.
[5]LIU Weidong, LIN Zhengyan.Precise Asymptotics for a New Kind of Complete Moment Convergence [J].Statist Probab Lett, 2006, 76(16): 1787-1799.
[6]刘君, 董志山, 张勇.由强混合序列生成线性过程精确渐近性的一般形式 [J].吉林大学学报: 理学版, 2008, 46(4): 595-600.(LIU Jun, DONG Zhishan, ZHANG Yong.A General Result on Precise Asymptotics for the Linear Process Generated by Strong Mixing Sequences [J].Journal of Jilin University: Science Edition, 2008, 46(4): 595-600.)
[7]SU Zhonggen.Precise Asymptotics for Random Matrices and Random Growth Models [J].Acta Math Sin: Engl Ser, 2008, 24(6): 971-982.
[8]ZHANG Yong, YANG Xiaoyun, DONG Zhishan.A General Law of Precise Asymptotics for the Complete Moment Convergence [J].Chin Ann Math: Ser B, 2009, 30(1): 77-90.
[9]FU Ke’ang, ZHANG Lixin.Pecise Rates in the Law of the Logarithm for the Moment Convergence in Hilbert Spaces [J].Acta Math Sin: Engl Ser, 2007, 23(6): 965-972.
[10]TAN Xili, YANG Xiaoyun.The Precise Asymptotics of the Complete Convergence for Moving Average Processes ofm-DependentB-Valued Elements [J].Acta Math Sin: Engl Ser, 2009, 25(3): 467-480.
[11]ZHANG Yong, YANG Xiaoyun, DONG Zhishan.A General Law of Precise Asymptotics for Products of Sums under Dependence [J].Acta Math Sin: Engl Ser, 2010, 26(1): 107-116.
[12]吴素文, 张勇, 李喜霞, 等.均匀经验过程精确渐近性的一个注记 [J].吉林大学学报: 理学版, 2011, 49(5): 844-848.(WU Suwen, ZHANG Yong, LI Xixia, et al.A Note on the Precise Asymptotics for Uniform Empirical Processes [J].Journal of Jilin University: Science Edition, 2011, 49(5): 844-848.)
[13]李云霞.长程相依过程关于矩完全收敛的精确渐近性质 [J].高校应用数学学报: A辑, 2013, 28(1): 23-33.(LI Yunxia.Precise Asymptotics for Complete Moment Convergence of Long Memory Processes [J].Appl Math J Chinese Univ: Ser A, 2013, 28(1): 23-33.)
[14]Gut A, Steinebach J.Precise Asymptotics: A General Approach [J].Acta Math Hungar, 2013, 138(4): 365-385.
[15]WANG Qiying, LIN Yanxia, Gulati C M.Asymptotics for Moving Average Processes with Dependent Innovations [J].Statist Probab Lett, 2001, 54(4): 347-356.
[16]WANG Qiying, LIN Yanxia, Gulati C M.Strong Approximation for Long Memory Processes with Applications [J].J Theoret Probab, 2003, 16(2): 377-389.
[17]WANG Lihong.Change-in-Mean Problem for Long Memory Time Series Models with Applications [J].J Stat Comput Simul, 2008, 78(7/8): 653-668.
[18]WU Weibiao, HUANG Yinxiao, ZHENG Wei.Covariances Estimation for Long-Memory Processes [J].Adv in Appl Probab, 2010, 42(1): 137-157.
[19]LI Yunxia, XU Jianjun, ZHANG Lixin.Testing for Changes in the Mean or Variance of Long Memory Processes [J].Acta Math Sin: Engl Ser, 2010, 26(12): 2443-2460.
[20]Palma W.On the Sample Mean of Locally Stationary Long-Memory Processes [J].J Statist Plann Inference, 2010, 140(12): 3764-3774.
[21]Beran J, Das B, Schell D.On Robust Tail Index Estimation for Linear Long-Memory Processes [J].J Time Series Anal, 2012, 33(3): 406-423.
[22]Khan M A R, Poskitt D S.Moment Tests for Window Length Selection in Singular Spectrum Analysis of Short-and Long-Memory Processes [J].J Time Series Anal, 2013, 34(2): 141-155.
[23]FU Ke’ang, Ng A C Y.A Note on the Strong Approximation for Long Memory Processes and Its Application [J].Statistics, 2013, 47(3): 511-520.
[24]Hall P, Heyde C C.Martingale Limit Theory and Its Application [M].New York: Academic Press, 1980.
GeneralResultofPreciseAsymptoticsforLongMemoryProcesses
GUAN Lihong, ZHAO Yanan
(SchoolofScience,ChangchunUniversity,Changchun130022,China)
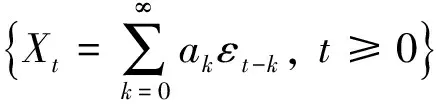
long memory process; complete moment convergence; precise asymptotics; general result; fractionally integrating process
2014-03-14.
关丽红(1976—), 女, 满族, 硕士, 讲师, 从事概率统计与应用数学的研究, E-mail: guanlihong14@163.com.
国家自然科学基金(批准号: 11371085)和吉林省教育厅“十二五”科技研究项目(批准号: 吉教科合字[2014]第526号).
O211.4
A
1671-5489(2014)06-1191-05
10.13413/j.cnki.jdxblxb.2014.06.16
赵立芹)
