α-混合序列生成的平稳线性过程矩完全收敛性的精确渐近性
2014-09-06邹广玉
邹 广 玉
(长春工程学院 理学院, 长春 130012)
α-混合序列生成的平稳线性过程矩完全收敛性的精确渐近性
邹 广 玉
(长春工程学院 理学院, 长春 130012)
利用α-混合序列的矩不等式及α-混合序列生成的平稳线性过程部分和的渐近分布, 得到α-混合序列生成的平稳线性过程部分和的矩完全收敛性的精确渐近性.
α-混合序列; 线性过程; 矩完全收敛性; 精确渐近性
0 引言及主要结果
设{εt;t∈}为定义在概率空间(Ω,F,P)的随机变量序列, 实数列{aj;j∈}满足|aj|<∞, 且定义线性过程目前, 关于线性过程的极限性质研究已取得许多结果, 如: 文献[1]得到了独立同分布序列生成线性过程二阶矩收敛的精确渐近性; 文献[2]讨论了NA序列生成线性过程的大偏差原理; 文献[3]对于一般的拟权函数和边界函数给出了PA列生成线性过程的精确渐近性; 文献[4]给出了鞅差序列生成平均移动过程的完全收敛性及Marcinwikiewcz-Zygmund强大数定律; 文献[5]讨论了φ-混合序列生成线性过程关于矩完全收敛的精确渐近性.
α-混合序列是诸多混合序列中限制条件较少的一种, 定义如下:
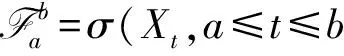
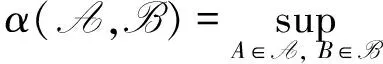
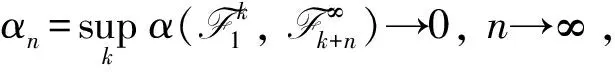
文献[6]得到了由α-混合序列生成线性过程精确渐近性的一般形式, 本文在此基础上讨论α-混合序列生成线性过程的矩完全收敛性的精确渐近性.
下面设{εj;j∈}为严平稳α-混合随机变量序列, 满足Eε1=0, 且对某个r>2,δ>0,E<∞, 混合系数满足
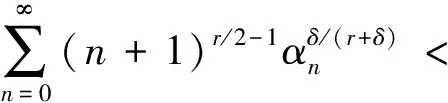
实数列{aj;j∈}满足|aj|<∞, 且线性过程设记
定理1
定理2对于0≤p<2, 有
1 引 理

证明可参见文献[7]中定理2.2.
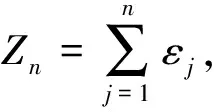
证明可参见文献[8]中推论1.
引理3在本文假设条件下, 存在不依赖于n的常数B, 使得对任意的n≥1, 有
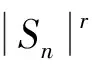
证明: 利用引理2, 类似文献[9]中引理4的证明可得结论.
2 定理的证明
不失一般性, 假设τ2=1.
2.1定理1的证明
记b(ε)=[ε-2].定理1可由以下几个命题推得.
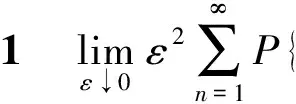
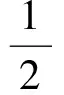
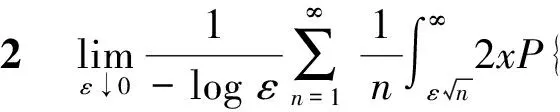
证明:
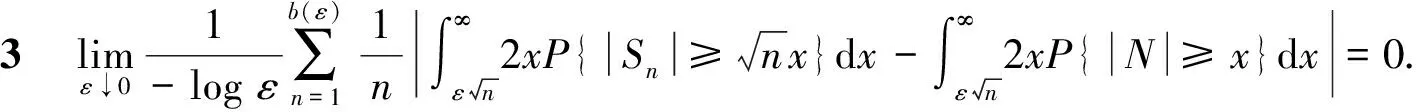
证明:
其中:
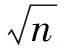
其次估计Δn2.由引理3和Markov不等式, 有
最后估计Δn3.由Markov不等式, 有
由引理1可得Δn→0(n→∞), 从而由式(3)~(5)有
再由式(6)及Toeplitz引理知命题3成立.
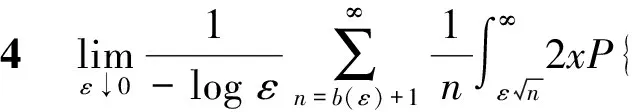
证明:
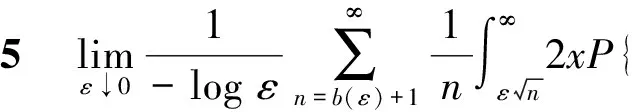
证明: 由Markov不等式及引理3, 有
下面证明定理1.由于
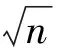
因此为了证明式(1), 只需证明下面两式成立:
由命题1可知式(7)成立, 由命题2~命题5及三角不等式可得式(8).从而定理1得证.
2.2定理2的证明
令d(ε)=[Mε-2],M≥1.定理2可由以下几个命题推得.
命题6当0 证明: 由文献[10]中命题4.1可得. 命题7当p>0时, 有 证明类似文献[5]中命题4.1的证明. 命题8当p>0时, 有 证明类似文献[5]中式(4.8)的证明. 命题9当p>0时, 有 |Sn|≥x}dx=0. 证明: 注意到r>2, 由Markov不等式及引理3, 有 下面证明定理2.由于当p=0时, 从而由命题1知此时定理2成立.因此只需验证当0 从而为了证明式(2), 只需证明下面两式成立: 由命题1可知式(9)成立, 由命题6~命题9及三角不等式可得式(10).从而定理2得证. [1]ZANG Qingpei.A Kind of Exact Rates in Complete Moment Convergence for Moving-Average Processes [J].Comm Statist: Theory and Methods, 2013, 42(13): 2464-2471. [2]杨小云, 董志山.NA及B-值随机变量序列的平均移动过程的大偏差原理 [J].应用概率统计, 2003, 19(4): 363-370.(YANG Xiaoyun, DONG Zhishan.Large Deviations for the Moving Average Processes of NA andB-Valued Random Variables [J].Chinese Journal of Applied Probability and Statistics, 2003, 19(4): 363-370.) [3]TAN Xili, YANG Xiaoyun.A General Result on Precise Asymptotics for Linear Process of Positively Associated Sequences [J].Appl Math J Chinese Univ: Ser B, 2008, 23(2): 190-196. [4]陈平炎, 李远梅.鞅差序列滑动和过程的极限结果 [J].数学物理学报, 2011, 31A(1): 179-187.(CHEN Pingyan, LI Yuanmei.Limiting Behavior of Moving Average Processes of Martingale Difference Sequences [J].Acta Mathematica Scientia, 2011, 31A(1): 179-187.) [5]LI Jie.Precise Asymptotics of Moving Average Process underφ-Mixing Assumption [J].J Korean Math Soc, 2012, 49(2): 235-249. [6]刘君, 董志山, 张勇.由强混合序列生成线性过程精确渐近性的一般形式 [J].吉林大学学报: 理学版, 2008, 46(4): 595-600.(LIU Jun, DONG Zhishan, ZHANG Yong.A General Result on Precise Asymptotics for the Linear Process Generated by Strong Mixing Sequences [J].Journal of Jilin University: Science Edition, 2008, 46(4): 595-600.) [7]Lee S Y.Random Central Limit Theorem for the Linear Process Generated by a Strong Mixing Process [J].Statist Probab Lett, 1997, 35(2): 189-196. [8]Yokoyama R.Moment Bounds for Stationary Mixing Sequences [J].Z Wahrsch Verw Gebiete, 1980, 52(1): 45-57. [9]曾艳, 王文胜.鞅差序列生成的线性过程的精确渐近性 [J].高师理科学刊, 2010, 30(4): 1-4.(ZENG Yan, WANG Wensheng.Precise Asymptotics for Linear Processes of Martingale Difference Sequences [J].Journal of Science of Teachers’ College and University, 2010, 30(4): 1-4.) [10]LIU Weidong, LIN Zhengyan.Precise Asymptotics for a New Kind of Complete Moment Convergence [J].Statist Probab Lett, 2006, 76(16): 1787-1799. PreciseAsymptoticsinCompleteMomentConvergenceforLinearProcessofα-MixingSequences ZOU Guangyu Applying the moment inequality ofα-mixing sequence and the asymptotic distribution for linear processes generated byα-mixing sequences, the author obtained some results on precise asymptotics in complete moment convergence for linear process generated byα-mixing sequences. α-mixing sequence; linear process; complete moment convergence; precise asymptotics 2014-02-28. 邹广玉(1982—), 男, 汉族, 博士, 讲师, 从事概率极限理论的研究, E-mail: jingyang999@126.com. 国家自然科学基金(批准号: 11401090)、吉林省教育厅项目(批准号: 120120113)和长春工程学院青年基金(批准号: 320130019). O211.4 A 1671-5489(2014)06-1186-05 10.13413/j.cnki.jdxblxb.2014.06.15 赵立芹)
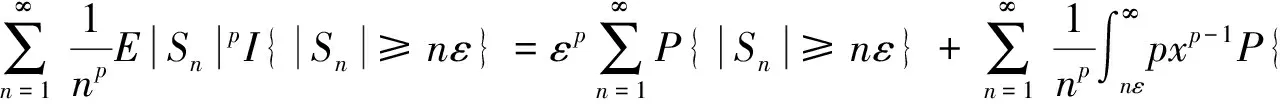
(SchoolofScience,ChangchunInstituteofTechnology,Changchun130012,China)
