赋广义Orlicz范数Orlicz函数空间的H点
2014-09-06王宏志段丽芬左明霞
王宏志, 段丽芬, 左明霞
(1.通化师范学院 数学学院, 吉林 通化 134002; 2.哈尔滨理工大学 应用科学学院, 哈尔滨 150080)
赋广义Orlicz范数Orlicz函数空间的H点
王宏志1, 段丽芬1, 左明霞2
(1.通化师范学院 数学学院, 吉林 通化 134002; 2.哈尔滨理工大学 应用科学学院, 哈尔滨 150080)
利用赋广义Orlicz范数Orlicz空间的结构特点, 借鉴经典Orlicz空间中H点的论证, 给出赋广义Orlicz范数Orlicz函数空间H点的判据, 并得到了赋广义Orlicz范数Orlicz函数空间具有H性质的一个充要条件.
广义Orlicz范数; Orlicz函数空间; H点; H性质
H点和H性质是Banach空间几何学的重要概念, 在概率论、控制论和逼近论等领域应用广泛[1-3].目前, 关于Banach空间H点和H性质的讨论已有很多结果[4-7].本文研究赋广义Orlicz范数Orlicz函数空间的H点, 得到了赋广义Orlicz范数的Orlicz函数空间H点的判据, 并获得了赋广义Orlicz范数Orlicz函数空间具有H性质的条件.
1 预备知识
设X是一个Banach空间,X′表示其共轭空间,S(X)表示X的单位球面.


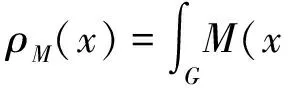
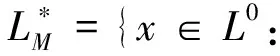
及其闭子空间
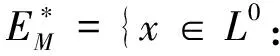
关于Orlicz范数:
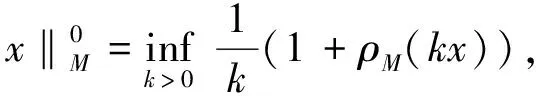
Luxemburg范数:
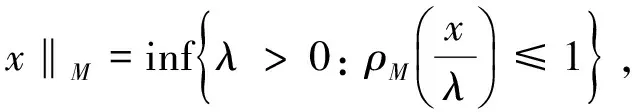
及广义Orlicz范数:
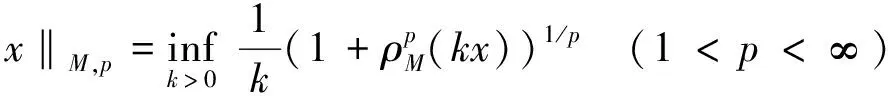
均成为Banach空间, 简记为
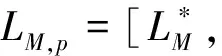
2 主要结果
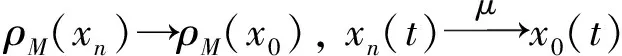
证明: 由文献[8]中定理1.41和文献[9]中定理1可得.
引理2设M是N-函数, 1 且kn→∞, 则: 证明: 1) 任给σ>0, 取Gn={t∈G: |xn(t)|≥σ}, 则 再由ε的任意性, 可得v(xn)→0(n→∞).证毕. 引理3设M是N-函数, 1 则: 证明: 1) 由引理2可知,k0=sup{kn:n=1,2,…}<∞.因为对一切正整数n,m, 都有 其中Gn(m)={t∈G: |knxn(t)|≥m}, 所以结论1)成立. 2) 若不然, 则存在δ>0及En⊂G(n=1,2,…), 使得 ρM(knxnχEn)≥δ>0,μEn<2-n(n=1,2,…). 取正整数m, 使得 矛盾. 引理4设M是严格凸的N-函数, 1 证明: 若不然, 不妨设对一切正整数n, 有 μ{t∈G: |knxn(t)-k0x0(t)|≥σ0}≥ε0, Gn={t∈G: |knxn(t)|≤D; |k0x0(t)|≤D; |knxn(t)-k0x0(t)|≥σ0} (n=1,2,…), M(αu+(1-α)v)≤(1-δ)[αM(u)+(1-α)M(v)]. 利用Minkowsky不等式即得 这与‖xn+x0‖M,p→2(n→∞)矛盾.证毕. 定理1设M是N-函数, 则对任何1 SM={u∈+: ∀ε>0, 2M(u) 证明: 必要性.由文献[10]中定理2.1、定理2.3及文献[9]中定理4可直接得到. 充分性.设M∈Δ2,x0∈S(LM,p)且μ{t∈G:k0x0(t)∈SM}=0, 需证对任何都有‖xn-x0‖M,p→0(n→∞).由引理2, 只需证明且kn→k0(n→∞), 其中kn满足 设{[ai,bi]}i表示M的所有构造仿射区间, 令 H={t∈G:k0x0(t)∈[ai,bi]}. G(i)={t∈G:k0x0(t)=ai},G′(i)={t∈G:k0x0(t)=bi}. 利用Jensen不等式, 可得 不妨设对一切正整数i,j, 都有G(i)∩G′(j)=Ø, 于是 由文献[9]中定理4、定理5和定理1可得: 定理2设M是N-函数, 则对任何1 [1]Diestel J.Geometry of Functional Analysis-Selected Topics [M].Berlin: Springer-Verlag, 1975. [2]Krasnoselskii M A, Rutickii Y B.Convex Function and Orlicz Spaces [M].Groningen: P Noordhoff Ltd, 1961. [3]张健, 王萍, 崔云安.Banach序列空间的若干点态性质 [J].哈尔滨师范大学自然科学学报, 2008, 24(1): 10-16.(ZHANG Jian, WANG Ping, CUI Yun’an.Some Pointwise Properties of Banach Space [J].Naturnal Sciences Journal of Harbin Normal University, 2008, 24(1): 10-16.) [4]孙丽环.Musielak-Orlicz函数空间的若干几何性质 [D].哈尔滨: 哈尔滨理工大学, 2006.(SUN Lihuan.Some Geometry Properties of the Musielak-Orlicz Function Space [D].Harbin: Harbin University of Science and Technology, 2006.) [5]ZUO Mingxia, CUI Yun’an.H-Property in Musielak-Orlicz Sequence Spaces [J].Journal of Natural Science of Heilongjiang University, 2003, 20(4): 5-10. [6]陈述涛, 王玉文.Orlicz空间的H性质 [J].数学年刊, 1987, 8A(1): 61-67.(CHEN Shutao, WANG Yuwen.H-Property of Orlicz Spaces [J].Chinese Ann Math, 1987, 8A(1): 61-67.) [7]王廷辅, 崔云安.关于Orlicz空间的H性质的注记 [J].数学物理学报, 1998, 18(2): 217-220.(WANG Tingfu, CUI Yun’an.Property(H) in Orlicz Function Space [J].Mathematica Acta Scientia, 1998, 18(2): 217-220.) [8]CHEN Shutao.Geometry of Orlicz Spaces [M].Warszawa: Dissertations Math, 1996. [9]段丽芬, 崔云安.赋广义Orlicz范数的Orlicz空间的端点 [J].浙江大学学报: 理学版, 2007, 34(3): 252-256.(DUAN Lifen, CUI Yun’an.Extreme Points in Orlicz Space Equipped with the Generalized Orlicz Norm [J].Journal of Zhejiang University: Science Edition, 2007, 34(3): 252-256.) [10]丛滢伊.广义Orlicz空间的H性质 [D].哈尔滨: 哈尔滨理工大学, 2012.(CONG Yingyi.H-Property of Generalized Orlicz Spaces [D].Harbin: Harbin University of Science and Technology, 2012.) H-PointsinOrliczFunctionSpacesEndowedwiththeGeneralizedOrliczNorm WANG Hongzhi1, DUAN Lifen1, ZUO Mingxia2 Based on the structural characteristics of the Orlicz function spaces endowed with the generalized Orlicz norm and the expositions of H-points in classical Orlicz spaces, the criteria of H-points in Orlicz function spaces endowed with the generalized Orlicz norm were presented.As its application, both sufficient and necessary conditions for H-property of these spaces were obtained. generalized Orlicz norm; Orlicz function space; H-point; H-property 2014-02-20. 王宏志(1975—), 男, 汉族, 硕士, 副教授, 从事Banach空间几何理论的研究, E-mail: whz-98@126.com. 国家自然科学基金(批准号: 11226127)和吉林省教育厅“十二五”科学技术研究项目(批准号: 吉教科合字[2011]第456号; 吉教科合字[2014]第400号). O177.3 A 1671-5489(2014)06-1181-05 10.13413/j.cnki.jdxblxb.2014.06.14 赵立芹)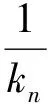
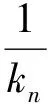
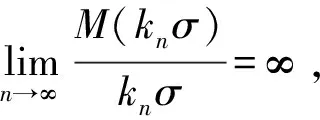
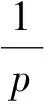
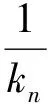
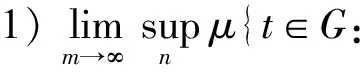
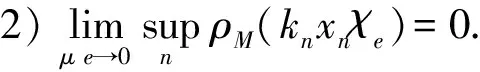

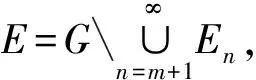
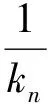
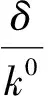
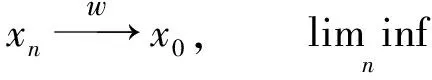
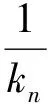
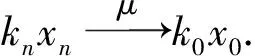


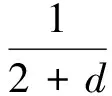
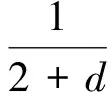
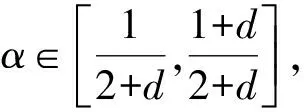
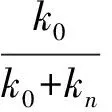
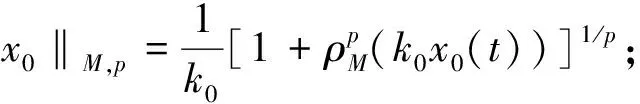
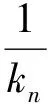
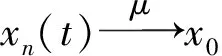
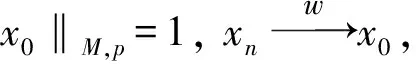
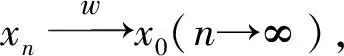

(1.CollegeofMathematics,TonghuaTeachersUniversity,Tonghua134002,JilinProvince,China;
2.CollegeofAppliedSciences,HarbinUniversityofScienceandTechnology,Harbin150080,China)
