多目标优化问题的同伦方法

王秀玉, 徐维华, 姜兴武, 戴嘉轩

(1.长春工业大学 基础科学学院, 长春 130012; 2.长春理工大学 理学院, 长春 130022;3.吉林工商学院 基础部, 长春 130062)

(1-μk)[f(x(k))λ(k)+gi(x(k))]+μk(x(k)-x(0))=0.(9)

多目标优化问题的同伦方法

王秀玉1, 徐维华2, 姜兴武3, 戴嘉轩1

(1.长春工业大学 基础科学学院, 长春 130012; 2.长春理工大学 理学院, 长春 130022;
3.吉林工商学院 基础部, 长春 130062)

用组合同伦方法求解带有不等式约束的多目标优化问题, 该同伦方法不要求可行域满足法锥条件, 且目标函数权重向量的初始值是非可行的.在上述条件下, 给出了同伦路径的存在性、有界性和收敛性的证明.

多目标优化问题; 同伦算法; 同伦路径

考虑如下多目标优化问题:

其中:x∈n;M={1,2,…,m};L={1,2,…,p};f=(f1,f2,…,fp)T:n→p,g=(g1,g2,…,gm)T:n→m均为充分光滑的向量值函数.

文献[1-4]对单目标的优化问题构造了组合同伦方法, 求解单目标问题的K-K-T点, 显示了同伦方法在求解优化问题中的优势.然而, 运用文献[1-4]中的组合同伦方法求解优化问题, 均需要可行域满足各类法锥条件, 从而使上述组合同伦方法的应用范围受到较大限制.

多目标优化问题应用广泛, 文献[5]将多目标问题转化为单目标问题, 建立了一种组合同伦方程, 对多目标问题的K-K-T点进行了求解, 将文献[1-4]的组合同伦方法推广到求解多目标优化问题, 但目标函数的权重保持不变.文献[6-8]改善了文献[5]的不足, 分别对可行域满足法锥条件、拟法锥及弱法锥条件时, 多目标问题K-K-T点的存在性和有界性进行了研究.文献[9]对凸多目标优化问题构造了动约束同伦方法, 并改进了权重向量为常向量的不足.但当可行域不满足任何法锥条件时, 如何运用文献[5-8]中的同伦方法求解多目标问题的K-K-T点, 目前尚未见文献报道.本文考虑只含有不等式约束的多目标规划问题, 且可行域不必满足任何法锥条件, 建立了同伦方程, 既克服了目标函数权重向量不变的不足, 又避免了法锥条件带来的局限性, 给出了同伦路径的存在性、有界性及收敛性证明.

1 同伦方程的构造及同伦路径的存在性

设x≥0(x>0)表示向量x的每个分量均为非负(正)数,f表示向量值函数f:n→n的Jacobi矩阵,h表示数量值函数h:n→的梯度, 其中n表示n维欧氏空间.

对问题(MOP), 本文对可行域实行外逼近方式, 使用下列符号: 0≤α<+∞为任意的非负常数;Ωα={x∈n|gi(x)≤α,i∈M}为关于α的可行域n|gi(x)<α,i∈M}为关于α的严格可行域表示Ωα的边界;Iα(x)={i|gi(x)=α,i∈M}表示点x∈Ωα的积极约束.当α=0时,Ω0即为多目标问题的可行域.

为求解问题(MOP), 做如下假设:

(H1)f(x),gi(x)(i∈M)是Cl(l≥3)函数;

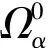
(H3) ∀x∈∂Ωα, {gi(x)|i∈Iα(x)}是正线性独立的,gi(x)=0,yi≥0⟹yi=0.

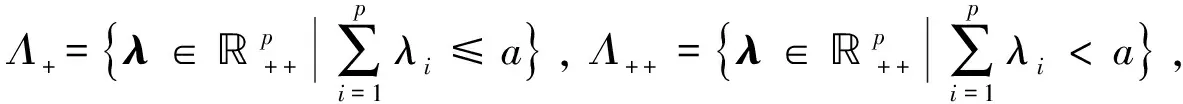
其中:Y=diag(y1,y2,…,ym);e=(1,1,…,1)T;ω=(x,y,λ).

当μ=1时, 式(1)有唯一解ω(0)=(x(0),y(0),λ(0)); 当μ=0时, 式(1)为

此即为多目标优化问题的K-K-T方程.显然H(ω(0),ω(0),1)=0.对给定的(x(0),y(0),λ(0)), 同伦方程(1)的左边H(ω,ω(0),μ)也记为Hω(0)(ω,μ), 并记

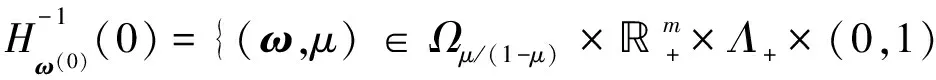
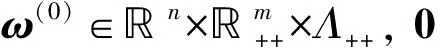
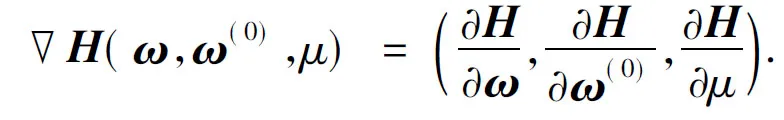
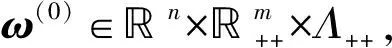
其中E为单位矩阵.由μ∈(0,1], 有

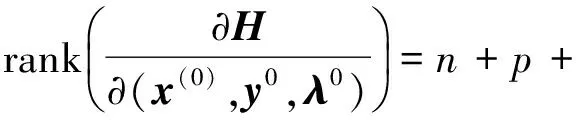
2 同伦路径的有界性和收敛性

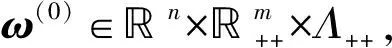
证明: 由同伦方程(1)的第二个方程可知, 若点(x,y,λ,μ)∈Γw(0), 则有

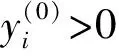
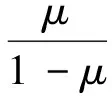
由同伦方程(1)的第三个方程可知

由式(4)可得

即

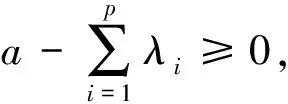
若Γω(0)无界, 则存在序列(x(k),y(k),λ(k),μk)∈Γω(0), 当k→∞时, 满足‖(x(k),y(k),λ(k),μk)‖→∞.由上述证明知{λ(k)}有界.

又由同伦方程(1)的第二个式子得

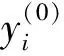
x(k)→x(*),λ(k)→λ(*),μk→μ*, ‖y(k)‖→∞.

若μk→1, 则由式(7)得y(k)→y(0), 这与y(k)的无界性矛盾, 因此有μk→/1, i.e.,μ*≠1.由式(8)得

即x(*)∈Ωμ*/(1-μ*).显然I⊆I(x(*)).由同伦方程(1)得

(1-μk)[f(x(k))λ(k)+gi(x(k))]+μk(x(k)-x(0))=0.(9)

即

（11）

式(11)与假设(H3)矛盾.

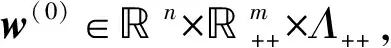
证明: 参考文献[7]中定理3的证明.由引理1和引理2知Γw(0)为有界光滑曲线.由一维流形分类定理知Γw(0)或者微分同胚于单位圆周, 或者微分同胚于单位区间(0,1].注意到

及

1)μ*∈[0,1),x(*)∈Ωμ*/(1-μ*),λ(*)∈Λ+, ‖y(*)‖→∞;

3)μ*=1,λ(*)∈Λ+,x(*)=x(0),y(*)=y(0);

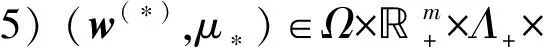
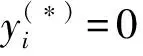
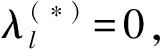
[1]YU Bo, FENG Guochen, ZHANG Shaoliang.The Aggregate Constraint Homotopy Method for Nonconvex Nonlinear Programming [J].Nonlinear Analysis: Theory Methods & Applications, 2001, 45(1): 839-847.

[2]YU Bo.A Combined Homotopy Infeasible Interior Point Method for Nonconvex Programming [J].Pacific J Optim, 2012, 8(1): 89-101.

[3]LIU Qinghuai, YU Bo, FENG Guochen.An Interior Point Path-Following Method for Nonconvex Programming with Quasi Normal Cone Condition [J].Advances in Mathematics, 2000, 29(4): 381-382.

[4]蔡志丹, 赵立芹, 苏孟龙.组合同伦内点算法求解一类非凸无界优化问题 [J].吉林大学学报: 理学版, 2013, 51(6): 1073-1076.(CAI Zhidan, ZHAO Liqin, SU Menglong.Combined Homotopy Interior Point Algorithm for a Class of Unbounded Non-convex Optimization Problems [J].Journal of Jilin University: Science Edition, 2013, 51(6): 1073-1076.)

[5]Song W, Yao G M.Homotopy Method for a General Multiobjective Programming Problem [J].Journal of Optimization Theory and Applications, 2008, 138(1): 139-153.

[6]赵雪, 张春阳, 张树功.弱拟法锥条件下解多目标规划问题的同伦方法 [J].吉林大学学报: 理学版, 2012, 50(4): 663-666.(ZHAO Xue, ZHANG Chunyang, ZHANG Shugong.Homotopy Method for Solving Multiobjective Programming Problem under Weak Quasi-normal Cone Condition [J].Journal of Jilin University: Science Edition, 2012, 50(4): 663-666.)

[7]ZHAO Xue, ZHANG Shugong, LIU Qinghuai.Homotopy Interior-Point Method for a General Multiobjective Programming Problem [J/OL].Journal of Applied Mathematics, 2012, doi: 10.1155/2012/497345.

[8]Zhao X, Zhang S G, Yang Y T, et al.Homotopy Method for a General Multiobjective Programming Problem under Generalized Quasinormal Cone Condition [J/OL].Abstract & Applied Analysis, 2012, doi:10.1155/2012/591612.

[9]SHANG Yufeng, YU Bo.A Constraint Shifting Homotopy Method for Convex Multi-objective Programming [J].Journal of Computational and Applied Mathematics, 2011, 236(5): 640-646.

HomotopyMethodforMultiobjectiveProgrammingProblems

WANG Xiuyu1, XU Weihua2, JIANG Xingwu3, DAI Jiaxuan1
(1.SchoolofBasicScience,ChangchunUniversityofTechnology,Changchun130012,China;
2.SchoolofScience,ChangchunUniversityofScienceandTechnology,Changchun130022,China;
3.DepartmentofBase,JilinBusinessandTechnologyCollege,Changchun130062,China)

The combined homotopy method was constructed for solving multiobjective programming problem with inequalities constraints.This method does not need that the feasible region satisfies the normal condition.And the initial weight vector of the objective function is infeasible.The existence, boundedness and convergence of the homotopy path were proved under the above mentioned conditions.

multiobjective programming problem; homotopy method; homotopy path

2013-12-03.

王秀玉(1965—), 女, 汉族, 硕士, 副教授, 从事最优化理论与算法的研究, E-mail: wangxiuyu.000@163.com.

国家自然科学基金(批准号: 10771020)和吉林省自然科学基金(批准号: 201215128; 20101597).

O221.2

A

1671-5489(2014)06-1176-05

10.13413/j.cnki.jdxblxb.2014.06.13

赵立芹)