美式回望看涨期权的有限元方法

张 琪, 高景璐

(吉林大学 数学学院, 长春 130012)

(uτ,v)+(ux,vx)-(κ2-1)(ux,v)+u1v1=(g,v)+f1v1, ∀v∈([0,xN+1]).(4)

美式回望看涨期权的有限元方法

张 琪, 高景璐

(吉林大学 数学学院, 长春 130012)

考虑美式回望看涨期权的定价问题, 先利用变网格有限元方法对Black-Scholes方程进行离散, 求出期权值, 再采用Newton迭代法给出最佳实施边界, 两种方法交替使用, 得到了相应的数值解.通过与二叉树方法进行比较表明, 该数值方法有效.

美式回望看涨期权； 变网格有限元方法； 最佳实施边界

0 引 言

美式回望期权是一类依赖于原生资产的最值期权, 它是一类抛物型自由边界模型, 对于美式回望期权数值方法的研究目前已有许多结果[1-6].本文主要考虑看涨期权, 它满足下列微分方程[7]:

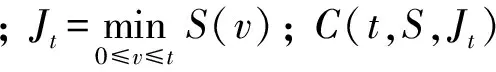
观察方程(1)可见, 该问题是反向变系数问题, 且关于空间方向是二阶的, 将导致问题的求解较困难, 为此本文做以下变换, 并将问题简化, 使得边界条件为零[9]:

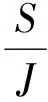
令κ1=2r/σ2,κ2=2(r-q)/σ2, 则方程(1)可变为

其中:

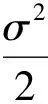
由于空间右端边界是与时间有关的函数, 无法应用一般有限元求解, 因此本文采用变网格方法结合有限元法, 即在每个时间层上应用有限元, 再利用u在τ时刻的值确定自由边界B(τ).先讨论B(τ).设uN=u(xN,τ)已知, 由于xN≤B(τ)[10], 则存在p使得B(τ)=xN+ph(h为网格步长), 利用方程(2)及Taylor展式可得p所满足的非线性方程：

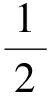
可以证明式(3)在区间[0,∞)上存在唯一解[8].

1 变网格有限元方法

下面主要对方程系统采用θ格式的有限元法进行离散化.

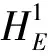
将变网格有限元法和Newton迭代法交替使用, 可逐步求出各时间层的函数值及最佳实施边界.

给定ε=10-6和p(0), 算法如下.

令p(0)=pm-1;

Forj=1,2,…;

1) 求解式(2)得到uN(pj-1);

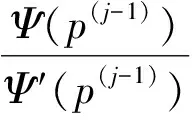
3) 如果|p(j)-p(j-1)|≤ε, 则终止循环;

2 M矩阵及稳定性分析

下面给出上述方法的理论分析[11].

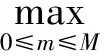
证明： 对于式(2)取v=um-θ, 则原式可化为

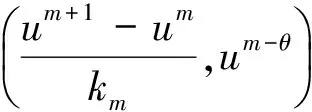
对于

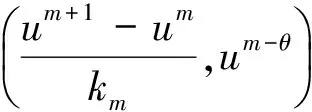
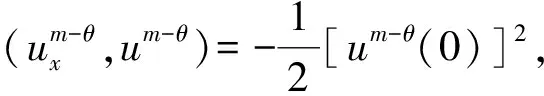
若假设成立, 结合边值条件um-θ(B)=0有

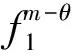
注意到f1(τ)=eκ1τ, 且um-θ(x1)有界, 故

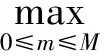
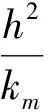
证明： 不失一般性, 本文只证明θ=1时(即隐格式)所形成的刚度阵为M矩阵, 式(2)可化为

不妨设所形成的刚度阵为A, 则有：

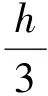
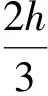
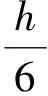
注意到当ρ充分小时,A为M矩阵, 故结论得证.

3 数值解法及应用实例

下面对一支美式回望看涨期权进行数值模拟.模型(1)中参数分别为r=0.1,q=0.05,σ=0.4, 空间间隔h=0.01, 时间份数M=512, 到期日T1=1, 参数θ=1.

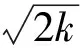
例2在上述条件下, 图2描述了在标的资产价格最小值m=1时, 期权价格C与S,t的函数关系.

图1 最佳实施边界B与时间τ的函数关系Fig.1 Relationship between the optimal exercise boundary B and time τ

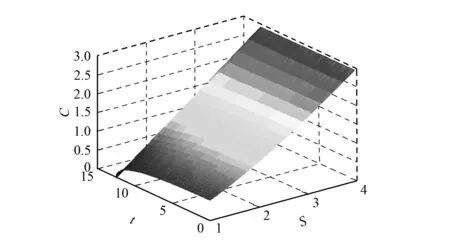
图2 期权价格关于原生资产和时间的函数关系Fig.2 Function of option price on underlying assets and time

[1]Babbs S.Binomial Valuation of Lookback Options [J].J Econ Dynam Control, 2000, 24(11/12): 1499-1525.

[2]Andricopoulos A D, Widdicks M, Duck P W, et al.Universal Option Valuation Using Quadrature Methods [J].J Financial Econ, 2003, 67(3): 447-471.

[3]Chang G H, Kang J K, Kim H S, et al.An Efficient Approximation Method for American Exotic Options [J].J Future Markets, 2007, 27(1): 29-59.

[4]Lai T L, Lim T W.Exercise Regions and Efficient Valuation of American Lookback Options [J].Math Finance, 2004, 14(2): 249-269.

[5]Hofer M, Mayer P.Pricing and Hedging of Lookback Options in Hyper-Exponential Jump Diffusion Models [J].Appl Math Finance, 2013, 20(5): 489-511.

[6]Heuwelyckx F.Convergence of European Lookback Options with Floating Strike in the Binomial Model [J].Int J Theor Appl Finance, 2014, 17(4): 1450025.

[7]JIANG Lishang, DAI Min.Convergence of Binomial Tree Method for European/American Path-Dependent Options [J].SIAM J Numer Anal, 2004, 42(3): 1094-1109.

[8]姜礼尚.期权定价的数学模型和方法 [M].北京: 高等教育出版社, 2003.(JIANG Lishang.Mathematical Modeling and Methods of Option Pricing [M].Beijing: Higher Education Press, 2003.)

[9]Pantazopoulos K N, Houstis E N, Kortesis S.Front-Tracking Finite Difference Methods for the Valuation of American Options [J].Comput Econ, 1998, 12(3): 255-273.

[10]DAI Min, Kwok Y K.American Options with Lookback Payoff [J].SIAM J Appl Math, 2005, 66(1): 206-227.

[11]Holmes A D, YANG Hongtao.A Front-Fixing Finite Element Method for the Valuation of American Options [J].SIAM J Sci Comput, 2008, 30(4): 2158-2180.

FiniteElementMethodfortheValuationofAmericanLookbackCallOption

ZHANG Qi, GAO Jinglu
(CollegeofMathematics,JilinUniversity,Changchun130012,China)

We analyzed American lookback call option valuation problem.Using the variable mesh finite element algorithm, we obtained the discrete form of the Black-Scholes equation, which is used to determine the value of American lookback option.Furthermore, we got the optimal exercise boundary using the Newton iterative method.When the two methods were alternately used, we gave corresponding numerical solutions.Finally, compared with the binomial method, this method is efficient and the theoretical analysis.

American lookback call option; variable mesh finite element algorithm; optimal exercise boundary

2014-03-28.

张 琪 (1988—), 女, 汉族, 博士研究生, 从事随机偏微分方程数值解的研究, E-mail： zqi13@mails.jlu.edu.cn.通信作者: 高景璐(1982—), 女, 汉族, 博士, 编辑, 从事偏微分方程数值及理论的研究, E-mail： jlgao@jlu.edu.cn.

国家自然科学基金(批准号: 11271157).

O241.8

A

1671-5489(2014)06-1167-04

10.13413/j.cnki.jdxblxb.2014.06.11

赵立芹)