超定非线性系统奇异解的可信验证

桑海风, 万保成

(1.北华大学 数学与统计学院, 吉林 吉林 132013; 2.吉林大学 数学学院, 长春 130012;3.吉林农业大学 信息技术学院, 长春 130118)

(f′(x*) R())=0, (f′(x*) R())=0.

超定非线性系统奇异解的可信验证

桑海风1,2, 万保成2,3

(1.北华大学 数学与统计学院, 吉林 吉林 132013; 2.吉林大学 数学学院, 长春 130012;
3.吉林农业大学 信息技术学院, 长春 130118)

利用边界矩阵和区间算法理论, 讨论超定系统奇异解的数值解法及其可信验证.提出一种新算法, 该算法输出一个近似解及其相应的误差界, 使得在近似解的误差界范围内必存在一个精确解.

超定非线性系统; 可信误差界; 奇异解

在密码学、机器人学和校准理论等领域中, 很多问题最终都可归结为超定非线性方程组的求解问题[1].因此, 超定非线性方程组解的可信验证是应用广泛的可信验证问题.Rump[2]首先给出了标准的可信验证方法, 该方法将浮点运算用于严格证明, 解决了非奇异问题的验证.对于奇异问题, 如验证非线性系统奇异解的存在性, 首先要将该系统正则化, 得到一个新的系统, 使得原来系统的奇异解成为新系统的解或者解的一部分, 然后再利用标准可信验证方法验证新系统的解.之后, Rump和Graillat[3]又提出了Jacobi矩阵秩亏为1的非线性系统二重根验证方法, 该方法通过将原方程组增加一个光滑变量, 并增加一个含n-1个变元、n个方程的方程组, 得到一个Jacobi矩阵非奇异的新系统, 将验证原方程组二重根的奇异问题转化为验证新系统单根的非奇异问题.Li等[4]研究了Jacobi矩阵秩亏为1的多项式系统孤立奇异解的可信验证, 通过将原方程组增加μ-1个光滑变量, 并增加μ-1个方程, 得到一个Jacobi矩阵非奇异的新系统, 也将验证原方程组孤立奇异解的奇异问题转化为验证新方程组单根的非奇异问题.

本文利用边界矩阵及区间算法理论, 讨论秩亏为q的超定非线性系统奇异解的数值解法及其可信验证, 给出了计算奇异解的一种数值算法和一种可信验证算法.如果数值算法输出超定系统的近似解, 则可信验证算法输出超定系统的一个近似解及其相应的误差界, 使得在近似解的误差界范围内必存在超定系统的一个精确解.特别地, 该验证算法不仅能验证孤立奇异点, 而且也能验证流形解上秩亏发生变化的点(即在该零点的任何一个小领域内, 相应Jacobi矩阵的秩都与该零点处Jacobi矩阵的秩不同).同时, 本文改进了文献[5]中计算边界系统Jacobi矩阵的方法, 使相应的计算量明显降低.

1 数值算法

记矩阵A的第i行为Ai,:=(Ai,1,…,Ai,n),q阶单位阵为Iq, 实数区间集合为I().令f:D⊂n→m(m>n)为超定非线性系统,x*∈n为f(x)=0的解,f′(x*)为f(x)在x*处的Jacobi矩阵.如果f′(x*)的秩为r=n-q, 则称f′(x*)秩亏为q(1≤q≤n), 并称x*为f(x)=0的奇异解.

本文假设所讨论的超定系统f满足下述条件:

(H1) 光滑性:f在x*的邻域内满足C2-Lipschitz条件;

(H2) 秩亏性:f′(x*)秩亏为q;

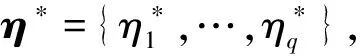
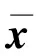
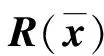
对足够接近x*的x, 令η(x)与h(x)为

的唯一解, 令μ(x)与g(x)为

的唯一解, 其中α为随机选取的m-n+q维向量.定义q×q阶矩阵

B(x,α)=ηT(x)(μT(x)f″(x))η(x).

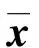
基于上述符号, 定义边界系统

其中λ为m-n+q维光滑参数.显然F(x,λ)的Jacobi矩阵为

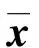
事实上,g′(x)可由求解下面线性方程组得到.任取j, 对式(2)关于变元xj求导得

其中∂g(x)/∂xj为g′(x)的第j列,j=1,2,…,n.

注1根据式(2)与式(5)知, 计算g′(x)只需求解n+1个具有相同系数阵的线性方程组即可.而文献[5]中g′(x)=ηT(x)(μT(x)f″(x)), 需计算q+1个方程组,q次3个矩阵乘积.故本文方法与文献[5]中方法相比计算量明显降低.特别地, 当矩阵为区间矩阵时, 计算量降低效果更显著.

由上述讨论及引理3, 可得:

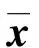
证明: 由式(1)及条件(H3)(η*为Null(f′(x*))的一组基), 有

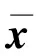
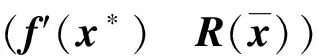
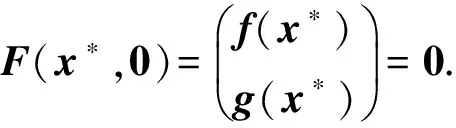
基于上述理论, 设计如下数值算法.

算法1边界系统的牛顿法.

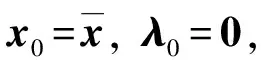
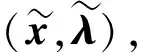
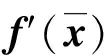
3) 随机选取q维向量α;

4) 若k>N, 则返回“失败”, 算法终止;

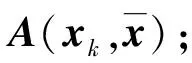
6) 利用式(3)及式(5), 分别计算g(xk)与g′(xk);

7) 利用式(3)及式(4), 分别计算F(xk,λk)与F′(xk,λk);

8) 计算

9) 若‖(Δxk,Δλk)‖2<ε2, 则返回(xk+1,λk+1)与q, 结束; 否则k∶=k+1, 返回步骤4).

2 可信验证算法

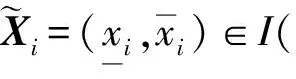
实现线性方程组解的可信验证函数是INTLAB中的Verifylss函数[7].对于系数阵为区间矩阵的线性方程组, Verifylss函数输出区间向量, 该区间向量包含此区间线性方程组所有可能的解.

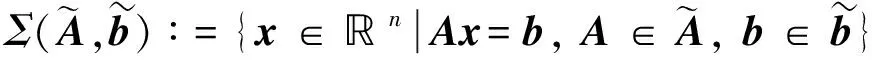
Moore[8]给出了非线性系统解存在性可验证的充分条件; Rump[9]进一步提出了标准的可信验证定理.

定理3[9]设函数f:D⊂n→n, 其中f=(f1,…,fn)∈C1.给定向量n, 区间向量n), 且以及矩阵T∈n×n, 且给定的区间矩阵n×n)满足条件{⊆.如果

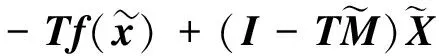
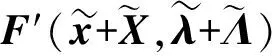
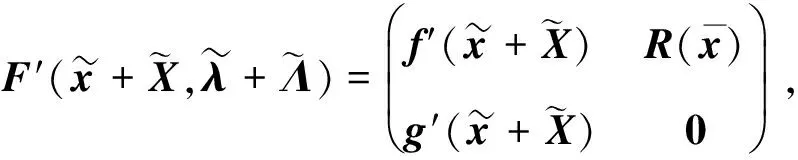
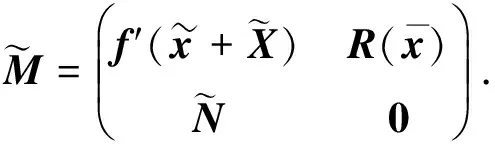
基于上述理论, 设计如下算法.

算法2可信验证算法.

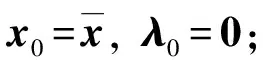
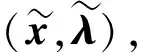
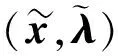
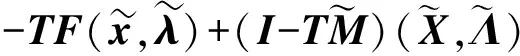
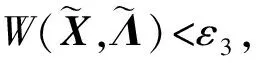
由定理3, 可得下述命题.

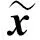
3 数值算例

下面的数值实验基于Windows 7操作系统, 软件分别是MAPLE 15(Digits∶=14)与MATLAB R2011a(INTLAB V6).对下列多项式系统执行上述隐式版可信验证算法, 可计算出非线性系统的近似解及相应的误差界.

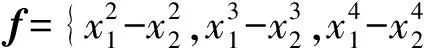
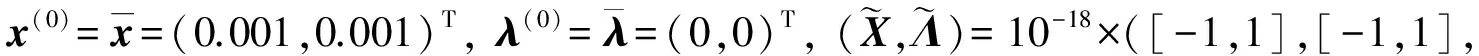
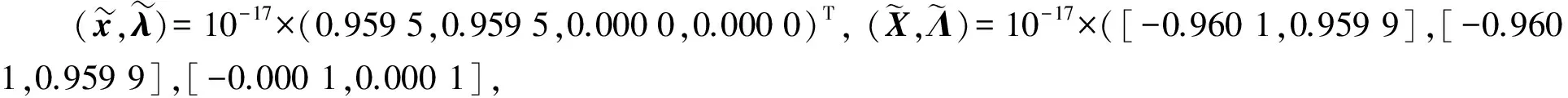
例1的解集为{x|x1-x2=0}, 奇异解x*=(0,0)嵌入流形x1=x2, 且f′(x)在点x*秩亏度比在其他解处的秩亏度高.

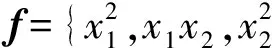
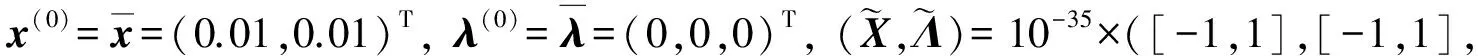
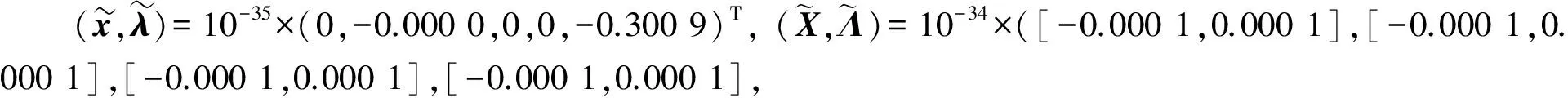
例2的解x*=(0,0)为孤立奇异点.

[1]Bardet M, Faugere J C, Salvy B.On the Complexity of Gröbner Basis Computation of Semi-regular Overdetermined Algebraic Equations [C]//Proceedings of the International Conference on Polynomial System Solving.Paris: University of Paris Press, 2004: 71-74.

[2]Rump S M.Kleine Fehlerschranken bei Matrixproblemen [D].Karlsruhe, German: Institut Fur Angewandte Mathematik, Universitat Karlsruhe, 1980.

[3]Rump S M, Graillat S.Verified Error Bounds for Multiple Roots of Systems of Nonlinear Equations [J].Numerical Algorithms, 2010, 54(3): 359-377.

[4]LI Nan, ZHI Lihong.Verified Error Bounds for Isolated Singular Solutions of Polynomial Systems: Case of Breadth One [J].Theoret Comput Sci, 2013, 479: 163-173.

[5]SHEN Yunqiu, Ypma T J.Newton’s Method for Singular Nonlinear Equations Using Approximate Left and Right Nullspaces of the Jacobian [J].Appl Numer Math, 2005, 54(2): 256-265.

[6]Moore R E, Cloud M J, Kearfott R B.Introduction to Interval Analysis [M].Philadelphia: SIAM Press, 2009.

[7]Rump S M.Verification Methods: Rigorous Results Using Floating-Point Arithmetic [J].Acta Numer, 2010, 19: 287-449.

[8]Moore R E.A Computational Test for Convergence of Iterative Methods for Nonlinear Systems [J].SIAM J Numer Anal, 1978, 15(6): 1194-1196.

[9]Rump S M.Solving Algebraic Problems with High Accuracy [C]//Proceedings of the Symposium on a New Approach to Scientific Computation.San Diego: Academic Press, 1983: 51-120.

VerifiedMethodsofSingularSolutionsofOverdeterminedNonlinearSystems

SANG Haifeng1,2, WAN Baocheng2,3
(1.CollegeofMathematicsandStatistics,BeihuaUniversity,Jilin132013,JilinProvince,China;
2.CollegeofMathematics,JilinUniversity,Changchun130012,China;
3.CollegeofInformationTechnology,JilinAgriculturalUniversity,Changchun130118,China)

We studied the numerical method and verification for singular points of overdetermined nonlinear equations.And we proposed an algorithm on the basis of the bordered system and interval theory.It outputs an approximate solution and its error bound so as to make an exact solution exist within this computed bounds.

overdetermined nonlinear system; verified error bound; singular solution

2014-02-07.

桑海风(1982—), 男, 汉族, 博士研究生, 讲师, 从事计算机代数的研究, E-mail: sanghaifeng2008@163.com.通信作者: 万保成(1977—), 男, 汉族, 博士研究生, 副教授, 从事计算机代数的研究, E-mail: wanbaocheng@163.com.

国家自然科学基金(批准号: 11171133)和吉林省教育厅科学技术研究项目(批准号: 2014213).

O242.29

A

1671-5489(2014)06-1162-05

10.13413/j.cnki.jdxblxb.2014.06.10

赵立芹)