α-稳定噪声驱动随机Cahn-Hilliard方程解的存在唯一性

贾秀利, 关丽红, 闫 龙

(1.吉林工商学院 基础部, 长春 130062; 2.长春大学 理学院, 长春 130022,3.吉林大学 数学研究所, 长春 130012)

α-稳定噪声驱动随机Cahn-Hilliard方程解的存在唯一性

贾秀利1, 关丽红2, 闫 龙3

(1.吉林工商学院 基础部, 长春 130062; 2.长春大学 理学院, 长春 130022,
3.吉林大学 数学研究所, 长春 130012)

利用压缩映射原理研究α-稳定噪声驱动的随机Cahn-Hilliard方程, 得到了该方程解的存在唯一性.

α-稳定噪声; 随机Cahn-Hilliard方程; 存在唯一性

0 引 言

Cahn-Hilliard方程[1]可模拟材料科学中二元合金相位分离的过程, 又称调幅分解.即二元合金的温度从T0淬火到临界温度Tc以下后, 二元合金分离成单质的过程.当该过程受到热干扰时, Prato等[2]研究了布朗运动驱动的随机Cahn-Hilliard方程, 给出了该方程解的性质; 文献[3-4]给出了该类方程解分布密度函数的性质.

近年来, Lévy噪声驱动的随机微分方程受到研究者的广泛关注[5-9].α-稳定噪声是一种特殊的Lévy噪声, 它能够展现重尾现象, 使得研究α-稳定噪声驱动的随机微分方程很有意义[10-12].考虑下述α-稳定噪声驱动的随机Cahn-Hilliard方程:

方程(1)满足初值条件u(0,·)=u0和齐次Neumann边值条件:

其中:T>0;D=[0,π]d;Lt是α-稳定噪声.α-稳定噪声驱动的随机Cahn-Hilliard方程描述材料科学中二元合金相位分离的过程, 其中:u表示二元合金相位分离率; 随机项Lt表示热扰动; Δu+f(u)表示化学势;f是首项系数为正的3次多项式,f的标准形式是3次多项式f(u)=u-u3; Neumann边值条件表示质量守恒和相位分离过程中与外部环境没有热交换.

方程(1)可用下列积分方程的形式表示[13]:

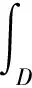
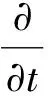
本文给出方程(1)解的存在唯一性.

1 预备知识

令H为实可分的Hilbert空间, 其内积为〈·,·〉0, H内的范数为‖·‖0.对于α∈(0,2), 令St是α/2-稳定的隶属子, 即递增的一维Lévy过程, 其Laplace变换为

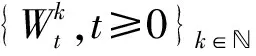
引理1[3]存在C>0和c>0, 1≤a≤3, 对于t∈(0,T],x,y∈D, 如下估计成立:

2 主要结果

假设:

(H1)f是一个主项系数为正的3次多项式;

(H2) 对于p≥2,

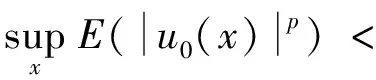
首先截断函数f, 使其在空间C([0,T];Lp(D))内, 当p≥3时是全局Lipschitz连续的; 其次证明截断方程的解弱收敛到原方程的解.

令n>0, 并且定义Ψn: [0,∞)→[0,1]是一个C1函数, 使得

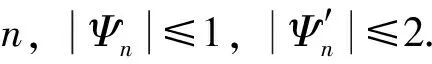
其中(t,x)∈[0,T]×D.

当p>3时, 令H为所有Lp(D)-值Ft适应的随机过程u(t,·)的空间, 其范数为‖·‖H,

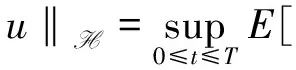
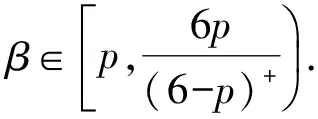
在空间H上定义非线性算子:

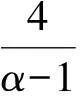
证明: 对于t∈[0,T], 利用引理1、Hölder不等式和文献[14]中定理3.2, 有

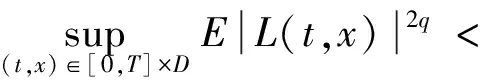
下面证明L(t,x)是Hölder连续的.对于任意的s,t∈[0,T],x,y∈D,

类似于式(12)的计算, 可得E‖L1‖p≤C(h)(t-s)(-d/4+d/(4α))p.再注意到

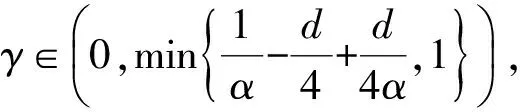
利用式(4),(5), 可得

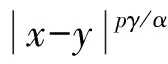
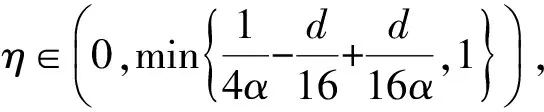
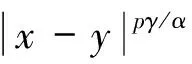
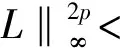
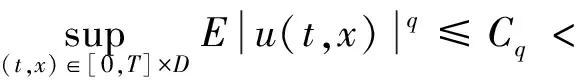
证明: 先证明当T足够小时, 算子Hn和L是压缩的.显然,

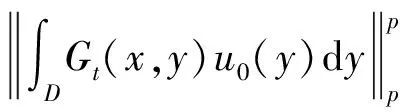
（13）

利用Cardon-Weber[3]中第785页的结果, 可知

‖Hn(u)(t,·)‖p≤C(n+1)3T1+d/(4r1)-(d+2)/4,

其中1≤r1<∞, 所以

‖Hn(u)(t,·)‖H≤∞.

（14）

另一方面, 由引理2, 对于任意的γ>1, 有

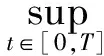
（15）

由式(13)～(15)可知,Hn和L是从H映到自身的映射.

利用Cardon-Weber[3]中第785页的结果, 可知

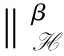
如果CnTβ((2-d)/4+d/(4r1))<1, 则Hn是H上的压缩映射.因此可得到方程在每个区间[0,T]内方程(9)解的存在唯一性.再利用Cardon-Weber[3]中第786～794页的结果可得方程全局解的存在唯一性.

[1]Cahn J W, Hilliard J E.Free Energy for a Nonuniform System.Ⅰ.Interfacial Free Energy [J].J Chem Phys, 1958, 28(2): 258-267.

[2]Prato G Da, Debussche A.Stochastic Cahn-Hilliard Equation [J].Nolinear Anal Th Meth Appl, 1996, 26: 241-263.

[3]Cardon-Weber C.Cahn-Hilliard Stochastic Equation: Existence of the Solution and of Its Density [J].Bernoulli, 2001, 7(5): 777-816.

[4]Cardon-Weber C.Cahn-Hilliard Stochastic Equation: Strict Positivity of the Density [J].Stoch Stoch Report, 2002, 72(3/4): 191-227.

[5]DONG Zhao, XIE Yingchao.Ergodicity of Stochastic 2D Navier-Stokes Equations with Lévy Noise [J].J Differ Equ, 2011, 251(1): 196-222.

[6]Dong Z, Xu T G.One-Dimensional Stochastic Burgers Equation Driven by Lévy Processes [J].J Funct Anal, 2007, 243(2): 631-678.

[7]Peszat S, Zabczyk J.Stochastic Partial Differential Equations with Lévy Noise: An Evolution Equation Approach(Encyclopedia of Mathematics and Its Applications) [M].Vol.113.Cambridge: Cambridge University Press, 2007.

[8]Priola E, Zabczyk J.Structural Properties of Semilinear SPDEs Driven by Cylindrical Stable Processes [J].Probab Theory Relat Fields, 2011, 149(1/2): 97-137.

[9]Priola E, Shirikyan A, XU Lihu, et al.Exponential Ergodicity and Regularity for Equations with Lévy Noise [J].Stoch Process Appl, 2012, 122(1): 106-133.

[10]DONG Zhao, XU Lihu, ZHANG Xicheng.Invariance Measures of Stochastic 2D Navier-Stokes Equations Driven byα-Stable Processes [J].Electron Commun Probab, 2011, 186: 122-152.

[11]XU Lihu.Ergodicity of the Stochastic Real Ginzburg-Landau Equation Driven byα-Stable Noises [J].Stochastic Process Appl, 2013, 123(10): 3710-3736.

[12]DONG Zhao, XU Lihu, ZHANG Xicheng.Exponential Ergodicity of Stochastic Burgers Equations Driven byα-Stable Processes [J].J Stat Phys, 2014, 154(4): 929-949.

[13]Walsh J B.An Introduction to Stochastic Partial Differential Equations [M].École d’Été de Probabilitése de Saint Flour ⅩⅣ.Lecture Note in Math.Vol.1180.Berlin: Springer, 1986: 265-439.

[14]ZHANG Xicheng.Derivative Formula and Gradient Estimate for SDEs Driven byα-Stable Processes [J].Stoch Process Appl, 2013, 123(4): 1213-1228.

ExistenceandUniquenessofSolutionsforStochasticCahn-HilliardEquationsDrivenbyα-StableNoise

JIA Xiuli1, GUAN Lihong2, YAN Long3
(1.DepartmentofBasicCourse,JilinBusinessandTechnologyCollege,Changchun130062,China;
2.CollegeofScience,ChangchunUniversity,Changchun130022,China;
3.InstituteofMathematics,JilinUniversity,Changchun130012,China)

Applying contracting mapping, we studied a class of stochastic Cahn-Hilliard equations driven byα-stable noise, and obtained the existence and uniqueness of solutions for the equations.

α-stable noise; stochastic Cahn-Hilliard equations; existence and uniqueness

2014-04-15.

贾秀利(1973—), 女, 汉族, 硕士, 副教授, 从事微分方程的研究, E-mail: jiaxiaoyi888@126.com.

国家自然科学基金(批准号: 11171130).

O211.63

A

1671-5489(2014)06-1151-04

10.13413/j.cnki.jdxblxb.2014.06.08

赵立芹)