具脉冲效应的非线性时滞抛物系统的振动分析
2014-09-06罗李平曾云辉罗振国
罗李平, 曾云辉, 罗振国
(衡阳师范学院 数学与计算科学系, 湖南 衡阳 421002)
具脉冲效应的非线性时滞抛物系统的振动分析
罗李平, 曾云辉, 罗振国
(衡阳师范学院 数学与计算科学系, 湖南 衡阳 421002)
利用新的处理非线性扩散项的技巧及脉冲时滞微分不等式, 研究一类具脉冲效应和非线性扩散项的时滞抛物系统在第一类边界条件下的振动性, 得到了该类系统所有解振动的若干新的充分性条件.结果表明, 系统振动是由脉冲和时滞效应引起的.
脉冲效应; 抛物系统; 振动性; 非线性扩散项; 时滞
0 引 言
脉冲现象在实际应用中普遍存在, 复杂动力系统网络中的节点特性和网络的拓扑结构中存在脉冲现象, 如Internet网络中传输的切换信号、节点之间的连接就具有脉冲特点.实际控制系统中普遍存在时滞现象, 而时滞常会导致控制系统性能的完全改变, 对于这种现象, 人们常用脉冲偏微分系统描述.脉冲控制因其易于操作及经济实用而被广泛应用, 可用于大型空间航天器的减震装置、卫星轨道的转换技术、机器人的研制、神经网络、混沌控制和保密通讯等.因此, 对脉冲偏微分系统理论的研究已引起人们广泛关注.振动性是系统运动的又一特征, 也是对系统内部特征“恢复力”的一种刻画.目前, 对脉冲偏微分系统解的振动性研究已取得了一些结果[1-9], 但关于具非线性扩散项脉冲偏微分系统解的振动性研究报道较少.
考虑一类具脉冲效应和非线性扩散项的时滞抛物偏微分系统:
及第一类边界条件:
ui=0, (t,x)∈+×∂Ω,t≠tk,k∈I∞,i∈Im,(3)
其中:Im={1,2,…,m};I∞={1,2,…};+=[0,∞);Ω⊂N是具有逐片光滑边界∂Ω的有界区域; Δ是N中的N维Laplace算子; 0 本文考虑系统(1)-(2)在第一类边界条件(3)下解的振动性, 利用积分平均技巧和脉冲时滞微分不等式, 获得了判别其所有解振动的不需要利用Dirichlet特征值问题的若干新的充分性判据.所得结果充分反映了脉冲量和时滞量在系统振动中的影响作用. 本文对系统(1)-(2)总假设下列条件成立: (H1)τr(t)∈C(+,(0,∞)), 且0<τr(t)<τ,r∈In; 其中:σ是正常数;bk>0为常数;k∈I∞; (H3)hi(ui),hir(ui)∈C1(,),uih(ui)≥0,uih(ui)≥0,hi(0)=0,hir(0)=0,i∈Im,r∈In. 定义1若对i∈Im,ui(t,x)满足下列条件: 3) 对t≠tk,x∈∂Ω,ui(t,x)满足式(3). 则称向量函数u(t,x)=(u1(t,x),u2(t,x),…,um(t,x))T为边值问题(1)-(3)的解. 定义2若数值函数ν(t,x):G→最终为正或最终为负, 则称其为非振动的; 反之, 称其为振动的.若向量函数u(t,x):G→m的每一分量都是非振动的, 则称其为非振动的; 若u(t,x)至少有一分量作为数值函数是振动的, 则称其为振动的. 定理1设存在常数β>0, 使得tk+1-tk≥β,k∈I∞, 且σ≥β.若 则边值问题(1)-(3)的所有解在区域G内振动. 证明: 反证法.假设边值问题(1)-(3)有一个非振动解u(t,x)=(u1(t,x),u2(t,x),…,um(t,x))T, 不失一般性, 设当t≥T>0时, 有|ui(t,x)|>0,i∈Im.令δi=sgnui(t,x), 则yi(t,x)=δiui(t,x)>0, (t,x)∈GT,i∈Im.令T1=T+max{τ,σ}, 则yi(t-τr(t),x)>0,yj(t-σ,x)>0, (t,x)∈GT1,i,j∈Im,r∈In. (i) 当t≥T1,t≠tk,k∈I∞时, 式(1)的第一式两边关于x在Ω上积分, 有 由Green公式、边值条件(3)及(H3), 有 其中: dS是∂Ω上的面积元素;v表示∂Ω的单位外法向量. 于是有 (ii) 当t≥T1,t=tk,k∈I∞时, 结合脉冲条件(2)及定义1中的条件1)可得 即 (10) 从而可知V(t)是脉冲时滞微分不等式(9),(10)的最终正解.由式(9)可知V′(t)≤-Q(t)V(t-σ)≤0,t≥T1,t≠tk.则当t≥T1,t≠tk时,V(t)在区间(tk,tk+1),k∈I∞上非增.对式(9)从tk到tk+β积分, 并注意到V(t)的非增性, 可得 类似定理1的证明可得如下结论: 定理3设存在常数β>0, 使得tk+1-tk≥β,k∈I∞, 且β>σ.若存在常数b>0, 使得0 则边值问题(1)-(3)的所有解在区域G内振动. 于是, 由式(13),(14)有 对充分大的t, 由式(9)可得 又由于 于是, 由式(15),(16)可得 这与条件(12)矛盾.证毕. 注1利用本文的方法可类似地讨论系统(1)-(2)满足其他边值条件(如第三类边界条件 其中β(x)∈C(∂Ω,(0,∞)))的所有解的振动结果.此时只要将假设条件(H3)改为: (H3)′hi(ui),hir(ui)∈C1(,+),uih(ui)≥0,uih(ui)≥0,i∈Im,r∈In. 例1考虑如下具非线性扩散项的脉冲时滞抛物系统: 边界条件为 [1]罗李平, 罗振国, 曾云辉.基于脉冲控制的非线性时滞双曲系统的振动分析 [J].系统科学与数学, 2013, 33(9): 1024-1032.(LUO Liping, LUO Zhenguo, ZENG Yunhui.Oscillation Analysis of Nonlinear Delay Hyperbolic Systems Based on Impulsive Control [J].J Sys Sci & Math Scis, 2013, 33(9): 1024-1032.) [2]LUO Liping, WANG Yanqun.Oscillation for Nonlinear Hyperbolic Equations with Influence of Impulse and Delay [J].Int J Nonlinear Sci, 2012, 14(1): 60-64. [3]罗李平, 俞元洪.具拟线性扩散系数的脉冲中立型抛物系统的(强)振动性 [J].振动与冲击, 2011, 30(8): 183-186.(LUO Liping, YU Yuanhong.(Strong) Oscillation for Systems of Impulsive Neutral Parabolic Equations with Quasilinear Diffusion Coefficient [J].Journal of Vibration and Shock, 2011, 30(8): 183-186.) [4]罗李平.具非线性扩散系数的脉冲时滞双曲型方程组的振动性 [J].自然科学进展, 2008, 18(3): 341-344.(LUO Liping.Oscillation of Systems of Impulsive Delay Hyperbolic Equations with Nonlinear Diffusion Coefficient [J].Progress of Natural Science, 2008, 18(3): 341-344.) [5]罗李平, 欧阳自根.脉冲中立型时滞抛物偏微分方程组的振动准则 [J].应用数学学报, 2007, 30(5): 822-830.(LUO Liping, OUYANG Zigen.Oscillation of Systems of Impulsive Neutral Delay Parabolic Equations about Boundary Value Problems [J].Acta Math Appl Sinica, 2007, 30(5): 822-830.) [6]罗李平, 欧阳自根.非线性脉冲中立型时滞抛物偏微分方程的振动性 [J].吉林大学学报: 理学版, 2007, 45(1): 23-28.(LUO Liping, OUYANG Zigen.Oscillation of Nonlinear Impulsive Neutral Delay Parabolic Partial Differential Equations [J].Journal of Jilin University: Science Edition, 2007, 45(1): 23-28.) [7]LUO Liping.Oscillation Theorem of Systems of Quasilinear Impulsive Delay Hyperbolic Equations [J].Northeast Math J, 2007, 23(3): 255-262. [8]ZHANG Yutian, LUO Qi.On the Forced Oscillation of Solutions for Systems of Impulsive Neutral Parabolic Differential Equations with Several Delays [J].J of Math, 2006, 26(3): 272-276. [9]LI Weinian.On the Forced Oscillation of Solutions for Systems of Impulsive Parabolic Differential Equations with Several Delays [J].J Comput Appl Math, 2005, 181(1): 46-57. OscillationAnalysisofNonlinearDelayParabolicSystemswithImpulseEffect LUO Liping, ZENG Yunhui, LUO Zhenguo Using a new technique of treating nonlinear diffusion term and impulsive delay differential inequalities, the authors studied the oscillation problems for a class of delay parabolic systems with impulse effect and nonlinear diffusion term under first boundary condition and some new sufficient conditions are established for the oscillation of all solutions of such systems.The results obtained fully indicate that the system oscillation is caused by the effect of impulse and delay. impulse effect; parabolic system; oscillation; nonlinear diffusion term; delay 2014-02-20. 罗李平(1964—), 男, 汉族, 教授, 从事脉冲微分系统解性态的研究, E-mail: luolp3456034@163.com. 湖南省自然科学基金青年项目(批准号: 13JJ4098)和湖南省“十二五”重点建设学科项目(批准号: 湘教发[2011]76号). O175.26 A 1671-5489(2014)06-1131-05 10.13413/j.cnki.jdxblxb.2014.06.05 赵立芹)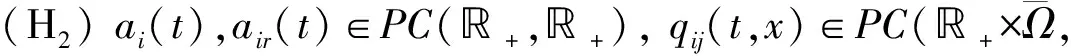
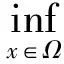
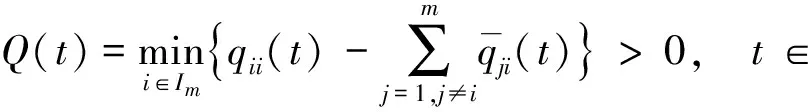
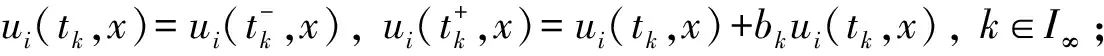
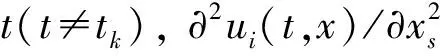
1 主要结果
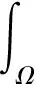
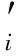
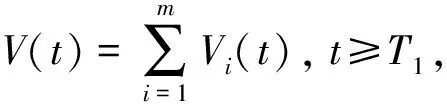

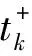
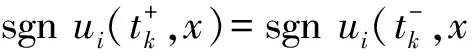
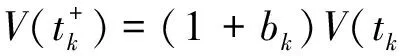
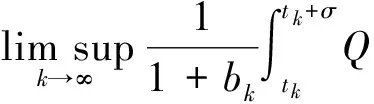
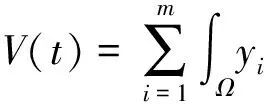
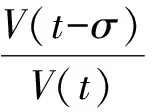
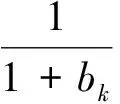
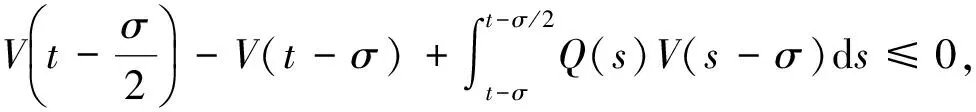
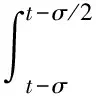
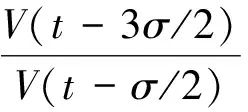
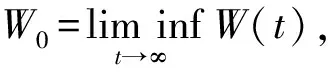

2 应 用

(DepartmentofMathematicsandComputationalScience,HengyangNormalUniversity,Hengyang421002,HunanProvince,China)
